§ 3. Начала математического анализа

Рассматриваются следующие задачи: вычисление пределов, дифференцирование функций одной и нескольких переменных, приложения дифференциального исчисления к исследованию функций.

Задача 27. Вычислить .

Решение. При числитель и знаменатель дроби неограниченно возрастают. В этом случае говорят, что имеет место неопределенность . Выносим за скобки в числителе и знаменателе переменную в старшей степени и после сокращения получаем:

.

При величины , , стремятся к 0, , весь числитель стремится к , а знаменатель . Поэтому вся дробь стремится к .

Таким образом,

Задача 28. Вычислить .

Решение. При числитель и знаменатель стремятся к . Это неопределенность вида . Раскрываем ее (см. задачу 27):

.

Задача 29. Вычислить .

Решение. Поскольку числитель и знаменатель при стремятся к , имеем неопределенность . Раскрываем ее (см. задачу 27):

.

Так как при числитель стремится к 3, а знаменатель − к , то вся дробь стремится к 0 и

.

Замечание. Полученные в задачах 27-29 результаты можно обобщить следующим образом:

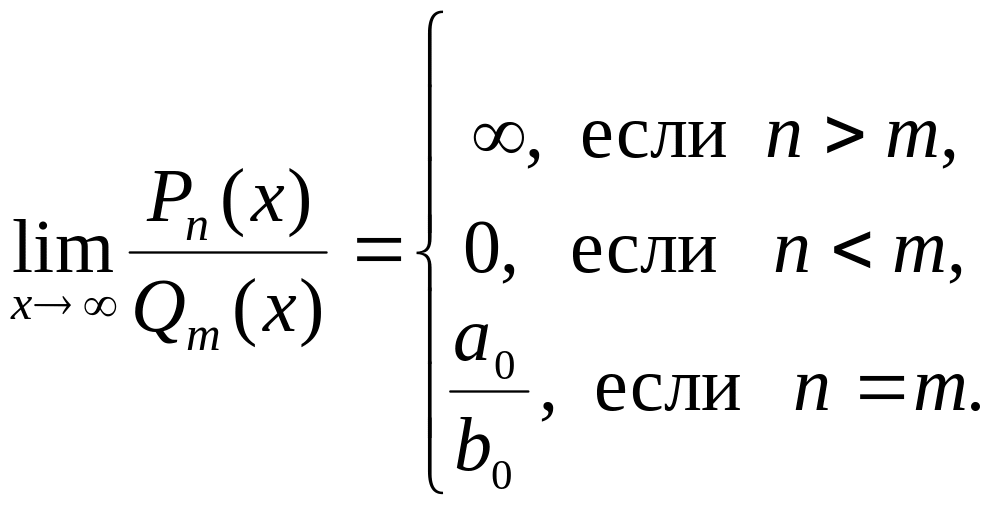
Здесь и - многочлены степеней n и m соответственно, причем

, .

Это правило позволяет сразу получить результат, минуя вычисления, одним лишь сравнением старших степеней многочленов числителя и знаменателя (в задаче 27: 5>2, значит, предел равен ; в задаче 28: 3 = 3, значит, предел равен ; в задаче 29: 1 < 2, значит, предел равен 0).

Задача 30. Вычислить .

Решение. При числитель и знаменатель дроби стремятся к 0. Это неопределенность вида . Разложив числитель и знаменатель на множители и выполнив сокращение на множитель (х − 7) (из-за которого и возникла неопределенность), получим

.

Задача 31. Вычислить .

Решение. Так как при выражение стремится к 1, а показатель степени − к бесконечности, имеем неопределенность . Раскрываем ее с помощью второго замечательного предела

.

Считая , достраиваем выражение до второго замечательного предела и получаем

.

Задача 32. Вычислить .

Решение. Поскольку при числитель и знаменатель дроби стремятся к 0, имеем неопределенность . Воспользовавшись формулами таблицы эквивалентности [приложение 4] для бесконечно малой величины ( ):

получим при :

Заменяя числитель и знаменатель на эквивалентные бесконечно малые величины, найдем

.

Задача 33. Вычислить .

Решение. Имеем неопределенность . Согласно формулам таблицы эквивалентности [приложение 4] для бесконечно малой величины ( )

поэтому при : .

Тогда

.

Задача 34. Найти , если .

Решение. Применяя формулы дифференцирования произведения и частного [приложение 4]:

,

имеем

и далее, с учетом формул дифференцирования элементарных функций (2),(5), (13) [приложение 4]

получим

.

Подставим в производную х = 2:

.

Задача 35. Для функции найти .

Решение. Применим правило дифференцирования сложной функции: если , , то .

В данном случае . Согласно формулам (12), (6) [приложение 4]

.

Тогда

.

Задача 36. Для функции найти .

Решение. По правилу дифференцирования сложной функции , где , имеем .

Так как , применяем формулы (7), (10) [приложение 4] :

.

Окончательно,

.

Задача 37. Дана функция Найти ее частные производные и в точке

Решение. Преобразуем данную функцию к виду

Вычислим частную производную , используя формулу дифференцирования (2) [приложение 4]

и считая у константой:

Подставив вместо х и у координаты точки , получим

Найдем , считая х константой:

Подставляя координаты точки , получим

Задача 38. Найти интервалы возрастания и убывания функции .

Решение. Функция y = f(x) возрастает, если , и убывает, если . Найдем :

.

Определим знаки первой производной и промежутки монотонности функции у

x		−1		0		1
	+	0	−	0	+	0	−
y

Итак, функция возрастает на интервалах и убывает на интервалах .

Задача 39. Найти интервалы выпуклости и вогнутости функции .

Решение. Функция выпукла, если и вогнута, если . Найдем :

,

.

Определим знаки второй производной и промежутки выпуклости и вогнутости функции у

x		−2		0		2
	−	0	+	0	−	0	+
y

Таким образом, функция выпукла при и вогнута при .