18. Условия равновесия произвольной (пространственной или плоской) системы сил
Необходимо и
достаточно, чтобы было
,
и относительно любого центра
было
.
Для пространственной системы сил
или, используя проекции на оси координат всех сил и их моментов относительно осей
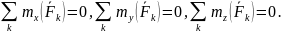
Для плоской системы сил
19. Теорема вариньона
Формулировка: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен сумме моментов сил относительно этого центра (рис. 56).
Рис. 56. Теорема Вариньона
Доказательство:
Система сил
,
,
… ,
заменяется равнодействующей
,
приложенной в некотором центре
.
Если приложить к
центру
дополнительную
силу
,
то система будет в равновесии. При этом
главный вектор
,
а при равновесии и главный момент
относительно центра
будет
.
Можно раскрыть
содержание величины
При
Тогда
что и требовалось доказать.
20. СЛОЖЕНИЕ ПАРАЛЛЕЛЬНЫХ СИЛ.
ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
Условия равновесия тела (рис. 57):
Рис. 57. Сложение параллельных сил
Рис. 58. Центр параллельных сил
Точка – центр параллельных сил (рис. 58).
Согласно теореме Вариньона в данном случае
или
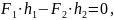
отсюда
21. КООРДИНАТЫ ЦЕНТРА СИЛ, ПАРАЛЛЕЛЬНЫХ ОДНОЙ ОСИ
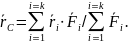
Согласно теореме Вариньона выполняется следующее равенство (рис. 59):
Рис. 59. Координаты центра тяжести
или
момент вокруг оси
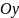будет
Отсюда
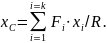
Аналогично
Если силы повернуть параллельно другой оси, например , то будет
22. КООРДИНАТЫ ЦЕНТРА ТЯЖЕСТИ ТЕЛА
Замечание.
Центр тяжести – это точка геометрическая. Она может быть вне тела, например, у кольца.
Для объёмных однородных тел
где
– удельный вес.
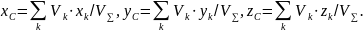
Для
плоских
тел с площадями каждого
Для участков однородной пространственной линии
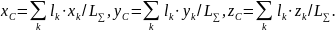
ДИНАМИКА
1. ВВЕДЕНИЕ В ДИНАМИКУ МАТЕРИАЛЬНОЙ ТОЧКИ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Динамика – описание движения тел под действием сил с учётом инертности масс тел.
Силы:
постоянные;
переменные.
Инертность – свойство тел сохранять движение при отсутствии сил.
Материальная точка – точка, имеющая массу; отвлечение от формы тела, когда оно не вращается.
2. ЗАКОНЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
Первый – закон инерции.
Второй – закон движения под действием сил или закон независимости действия сил:
Третий – закон равенства действия и противодействия.
3. ДВЕ ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
Для свободной точки:
1) основная (прямая): даны силы, определяется закон движения;
2) обратная: дан закон движения, определяются силы.
Для несвободной точки:
1) основная (прямая): даны только активные силы, определяется закон движения и реакции связей;
2) обратная: даны закон движения и активные силы, определяются только реакции связей.
4. СЛУЧАИ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Рис. 60. Прямолинейное движение материальной точки
Закон движения (рис. 60):
начальные условия:
начальные условия:
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ (СВОБОДНОЕ ПАДЕНИЕ БЕЗ УЧЁТА СОПРОТИВЛЕНИЯ)
Рис. 61. Свободное падение материальной точки без учёта сопротивления
Начальные условия (рис. 61):
.
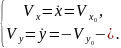
В конечной точке
при
:
Уравнение траектории
получается подстановкой в уравнение
выражения
через
.