9. Определение закона равнопеременного вращательного движения

отсюда

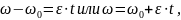
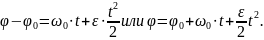
10. ВЫРАЖЕНИЕ ЛИНЕЙНОЙ СКОРОСТИ И

ЛИНЕЙНЫХ УСКОРЕНИЙ ТВЁРДОГО ТЕЛА

ЧЕРЕЗ ХАРАКТЕРИСТИКИ ВРАЩЕНИЯ

В твёрдом теле рассматривается некоторая точка , расположенная на расстоянии от оси вращения .

Рис. 14. Полное линейное ускорение вращающегося тела

11. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА. ОБЩЕЕ ОПРЕДЕЛЕНИЕ, ПРИМЕРЫ

Плоскопараллельным (ПП) или плоским называется такое движение, когда все точки тела перемещаются параллельно некоторой плоскости (рис. 15).

Примеры:

1) колесо на прямом участке пути;

2) вращение тела вокруг неподвижной оси;

3) движение шатуна в кривошипно-ползунном механизме.

Закон ПП движения

Рис. 15. Плоскопараллельное движение твёрдого тела

Частные случаи ПП движения

1) – поступательное движение;

2) (полюс неподвижен), но есть – вращение вокруг полюса .

Общий случай ПП движения: движение вместе с полюсом и вращение вокруг этого полюса.

Характеристики ПП движения:

12. ОПРЕДЕЛЕНИЕ ВЕКТОРА ЛИНЕЙНОЙ СКОРОСТИ НЕКОТОРОЙ ТОЧКИ ТВЁРДОГО ТЕЛА ПРИ ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИИ

Рис. 16. Определение линейной скорости некоторой точки

.

13. ТЕОРЕМА О ПРОЕКЦИЯХ НА ОДНУ ОСЬ СКОРОСТЕЙ ДВУХ ТОЧЕК ТВЁРДОГО ТЕЛА

Проекции на одну ось скоростей двух точек и тела, совершающего ПП движение, равны (рис. 17)

Доказательство от противного:

Если бы вышеприведённое равенство не выполнялось, то расстояние между точками А и В должно изменяться, а для твёрдого тела это невозможно.

Рис. 17. Теорема о проекциях на одну ось скоростей двух точек твёрдого тела

14. ОПРЕДЕЛЕНИЕ ВЕКТОРА ЛИНЕЙНОГО УСКОРЕНИЯ НЕКОТОРОЙ ТОЧКИ ТВЁРДОГО ТЕЛА ПРИ ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИИ

Рис. 18. Определение линейного ускорения некоторой точки

(рис. 27).

15. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ (МЦС) ПЛОСКОЙ ФИГУРЫ. ОБЩЕЕ ОПРЕДЕЛЕНИЕ

МЦС плоской фигуры – это точка, скорость которой в данный момент времени равно нолю. МЦС – точка (полюс) находится на пересечении перпендикуляров к векторам скоростей каких-либо двух точек плоской фигуры или к векторам скоростей концов линейного звена механизма, если это звено совершает плоскопараллельное движение.

Зная положение точки , можно определить направление и вычислить линейную скорость любой точки плоской фигуры.

Рис. 19. Мгновенный центр скоростей плоской фигуры

Со схемы (рис. 19) графически получаются значения и . Из пропорции, определяющей общую угловую скорость

вычисляется скорость

Частные случаи определения мцс

1. Качение без скольжения (рис. 20)

Рис. 20. Качение без скольжения

2. Поступательное движение (рис. 21)

Рис. 21. Поступательное движение

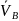Векторы и параллельны и равны по величине. Следовательно МЦС находится в бесконечности.

Полезные соотношения:

1. Известны значения , , 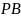(рис. 22).

Рис. 22. Определение скорости точки звена

Из пропорции

вычисляется значение

2. Если известны значения и , то вычисляется расстояние до МЦС (рис. 23)

Рис. 23. Определение расстояния до мгновенного центра скоростей