3.7. Уточнение высоты сечения ригеля.

Высота сечения ригеля определяется из условия возможного образования пластического шарнира:

,

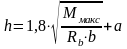где 1,8 – коэффициент, соответствующий рекомендуемому оптимальному значению относительной высоты сжатой зоны бетона.

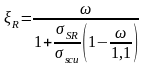
ω= α –0,008R_b=0,85–0,008·7,65=0,7883

α=0,85

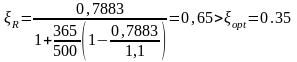
ξ_opt=0,35< ξ_R=0,65 т.е. условие ξ  ξ_R соблюдается

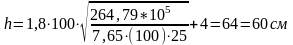
Окончательно принимаем h=60 см, b=25 см.

3.8. Расчет прочности ригеля по сечениям, нормальным к продольной оси (подбор продольной арматуры).

Сечение на крайней опоре: М=191,62 кН·м

Рабочая высота сечения ригеля при однорядном расположении стержней:

h₀ = h – a = 60-4 = 56м

ξ=0,42< ξ_R=0,65 , т.е. условие ξ  ξ_R соблюдается

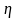=0,79

,

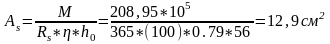228 А-III; А_s= 12,32 см²

Сечение на средней опоре: М=264,79 кНм

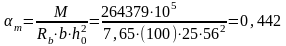
=0,67

,

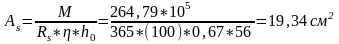425 А-III; А_s=19,68 см²

Сечение в пролете: М=199,96 кНм

Рабочая высота сечения при расположении арматуры в два ряда:

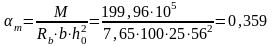
=0,765

,

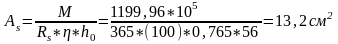420 А-III; А_s=12,56 см²

Так как в пролетах отсутствуют отрицательные моменты, то верхнюю зону ригеля армируем конструктивно:

212 А-III; А_s=2,26 см²

3.9.Расчет прочности ригеля по сечениям, наклонным к продольной оси (подбор поперечной арматуры).

В качестве расчетного принимаем сечение на средней опоре, в котором действует максимальная поперечная сила Q_max=262,46 кН, что больше

Q≤ 2,5R_btbh₀=2,5·0,675·250·560=236,25 кН

При диаметре продольной арматуре d=28мм принимаем диаметр поперечных стержней из условия свариваемости d_SW=8мм А-I. Так как число хомутов - 2 , то площадь сечения поперечных стержней равна А_SW=20,503=1,01 см²

Длина проекции опасной наклонной трещины на продольную ось ригеля предварительно определяется выражением

С₀ = 2·h = 2·56 = 112 см

Коэффициент, учитывающие вид бетона: для тяжелого бетона φ_b2 = 2,0; φ_b3 = 0,6.

Минимальная поперечная сила:

Q_b.min= φ_b3R_btbh₀ = 0,6·0,675·(100) ·25·56=56700Н

Момент поперечной силы:

М_b = φ_b2R_btbh₀² = 2·0,675·(100) ·25·56²=10584·10³ Н·см

Усилие в хомутах на единицу длины элемента в пределах наклонного сечения определяется как большее из следующих двух условий:

q_swQ²/4M_g = (262,46*10³)²/4*10584*10² = 1627,12 Н/см

q_sw Q_b.min /с₀ = 56700/112=506,25 Н/см

Расчетное усилие q_sw = 1627,12 Н/см распределяется на участке длиной, равной шагу поперечных стержней:

S =A_sw*R_sw/ q_sw = 175 (100) 1,01/1627,12=10,9 см

Максимальный допустимый шаг:

S_мах =0,75М_b/ Q= 0,75*10584*10³/262,46*10³=30,3 см

Определим шаг стержней исходя из конструктивных требований. При h400 мм Sh/3=60/3=20 см и не более 500мм. На приопорных участках равных 1/3 пролета принимаем S=20 см. В средней части пролета, равной L/2 шаг поперечных стержней S3/4h=3·60/4=45 см, но также не более 500мм.

Принимаем S(1)=20см.

q_sw=A_sw*R_sw/S=175*100*1,01/20=883,75 Н/см

Проверка прочности наклонного сечения:

Q= 262,46*10³˂2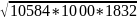 =278,5*10³ Н

Прочность наклонного сечения обеспечена.

Произведем проверку прочности наклонной сжатой полосы между наклонными трещинами:

Отношение модулей упругости

α=E_s/E_b=2,1·10⁵/2,3·10⁴=9,13

Коэффициент поперечного армирования по длине

μ_ω=A_s/b·S=1,01/25·20=0,00202

Коэф. учитывающий влияние хомутов

φ_ω1=1+5·6,46·0,00202=1,011,3

Коэф. оценивающий способность различных видов бетона

φ_b1=1–β R_b=1–0,01·7,65=0,9235

β=0,01 для тяжелого бетона

Проверка прочности по сжатой полосе между наклонными трещинами

Q=0,3·1,01·0,9235·7,65·100·25·56=335,29 кН

Q=217,94 кН  Q=335,29 кН

Условие выполняется, прочность обеспечивается.