МИНИСЕТРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

МЕЖДУНАРОДНАЯ ОБРАЗОВАТЕЛЬНАЯ КООРПОРАЦИЯ

ФАКУЛЬТЕТ ОБЩЕГО СТРОИТЕЛЬСТВА

Курсовой проект

по дисциплине: Проектирование и расчет железобетонных конструкций II

«Расчет и конструирование несущих конструкций многоэтажного здания»

Выполнил: студент группы

Кашкынбай А.С.

ЗСтр(ТПГС)-12-2

Проверил: ассоц. проф.

Келемешов А.Д.

Алматы 2017 г.

Исходные данные для проектирования

• Размеры здания в плане — 21 х 56 мхм

• Сетка колонн – 5,4 х 8,0 мхм

• Высота этажа — 3,3 м

• Размеры сечений колонн — 40 х 40 см

• Нормативная временная нагрузка — 7,5 кН/м²

• Длина ригеля — 7,8 м

• Шаг ригелей — 5 м

• Материал для ригеля: бетон класса В25, арматура из стали класса А-II

Расчет и конструирование сборного железобетонного ригеля

1. Определение расчетных сопротивлений арматуры и бетона

Ригель изготовляется из тяжелого бетона, подвергнутого тепловой обработке при атмосферном давлении, класса В25; коэффициент условий работы бетона γ_b2=0,9. R_b=18,5·0,9=7,65 МПа, R_bt=0,75·0,9=0,945 МПа.

Модуль упругости бетона E_b=24·10³МПа.

Поперечная арматура класса А-II:

R_s=365МПа, E_s=2·10⁵ МПа.

Продольная арматура класса А-I:

R_sw=225МПа, E_s=2,1·10⁵ МПа.

3.2. Установление расчетной схемы и величины пролетов ригеля

Ригель рассчитывают как трехпролетную неразрезную балку. За расчетный размер пролетов ригеля принимается расстояние между осями колонн L=7,8м.

3.3. Назначение предварительных размеров поперечного сечения ригеля.

Для определения собственного веса ригеля задаются размерами поперечного сечения:

h=(1/12…1/15)L=(1/13)780=60см. Принимаем h=60см.

b=0,5h=0,5∙60=25см. Принимаем b=25см.

3.4.Определение расчетных постоянной и временной нагрузок на 1пог.м ригеля.

Нагрузка на ригель от панелей при числе ребер панелей в пролете ригеля более четырех считается равномерно распределенной.

Подсчет нагрузок в таблице 1.

таблица 1

Вид нагрузки	Нормативная нагрузка, кН/м2	Коэффициент надежности по нагрузке	Расчетная нагрузка, кН/м2
Плиточный пол Выравнивающий пол толщиной 20 мм и плотностью 20 кН/м Ребристая плита перекрытия	0,3 0,4 2,5	1,1 1,3 1,1	0,33 0,52 2,75
Постоянная нагрузка	3,2	-	3,60
Временная нагрузка	7,5	1,2	9

Расчетные нагрузки на 1м длины ригеля определяются путем умножения расчетных нагрузок на ширину грузовой площади, равной шагу ригелей:

-собственный вес панели и пола: 3,6∙5=18 кН/м

-собственный вес ригеля: b∙h∙∙g_f=0,25∙0,6∙25∙1,1=4,125 кН/м

Полная постоянная нагрузка с учетом коэффициента надежности по назначению _n=0,95:

g = (18 + 4,125)·0,95=20,4 кН/м

Временная расчетная нагрузка:

v = 9∙5∙0,95 = 42,75 кН/м

Полная расчетная нагрузка:

q=g+v=20,4+42,75=63,15 кН/м

3.5.Статический расчет ригеля.

Усилия в ригеле – изгибающий момент и поперечную силу получают в результате статического расчет, произведенного по правилам строительной механики, как упругой системы.

Опорные моменты ригелей определяются по формуле, при равномерно распределенной нагрузке:

,

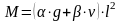где  и  – табличные коэффициенты, зависящие от схемы загружения ригеля нагрузками g и v, а также от отношения погонных жестокостей ригеля и стойки (колонны):

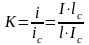
Ведем расчет ригеля крайнего пролета средней рамы, поскольку порядок расчета остальных пролетов аналогичен. Значения изгибающих моментов в средних пролетах многопролетных рам принимают по среднему пролету трех пролетной рамы.

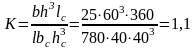
Табл.2

№ пп	Схема загружения		М12=Мл , кНм	М21=Мп , кНм
1			-0,062120,47,82= -77,08	-0,091220,47,82 = -113,19
2			-0,069242,757,82= -179,98	-0,073442,757,82= -190,91
3			0,007142,757,82= 18,47	-0,017842,757,82= -46,3
4			-0,06142,757,82= -158,66	-0,095642,757,82= -248,64
Комбинации нагрузок		1+2	-257,06	-304,1
		1+3	-58,61	-159,49
		1+4	-235,74	-361,83

Значения изгибающих моментов М_х в пролете на расстоянии х от левой опоры и поперечных сил Q на опорах определяются, как в балках, с учетом действительной нагрузки q и найденных по таблице опорных моментов при различных сочетаниях нагрузок:

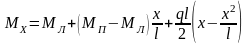
q=g+v или q=g , т.е. в зависимости от схем загружений для незагруженных пролетов должна учитываться только постоянная равномерно распределенная нагрузка.

Сечение в пролете ригеля, где возникает максимальный изгибающий момент М_u , определяется из условия Q_x=dM_x/dx=0 и находится на расстоянии x_u от левой опоры.

x_u=Q_Л/q

табл.3

x,м	Мх,кНм
	1+2	1+3	1+4		добавочная эпюра		перераспределенная эпюра
	q,кНм
	63,15	20,4	63,15
0,0	-257,06	-58,61	-235,74		-16,49		-252,23
0,78	-88,87	-12,85	-75,6		-8,89		-84,49
1,56	40,89	20,51	46,39		-3,29		43,1
2,34	132,25	41,45	129,85		3,31		133,16
3,12	185,18	49,99	174,86		9,91		184,77
3,9	199,69	46,1	181,46		16,5		197,96
4,68	175,76	29,8	149,63		23,1		172,73
5,46	113,44	1,11	79,39		29,7		109,09
6,24	12,67	-40	-29,28		36,3		7,02
7,02	-126,5	-93,54	-176,38		42,93		-133,45
7,8	-304,1	-159,49	-361,83		49,47		-312,36

Вычисленные значения поперечных сил и максимальных пролетных моментов сведены в таблице4

Табл.4

	Mлев	Mпр	q	Qлев	Qпр	xи	Ми
1+2	-257,06	-304,1	63,15	240,56	-252,32	3,8	19,96
1+3	-58,61	-159,49	20,4	66,63	-92,49	3,3	50,18
1+4	-235,74	-361,83	63,15	230,12	-262,46	3,6	183,48