2. 2 Номер

Билет 15

1. Функцией распределения вероятностей F(x) случайной величины Х в точке х называется вероятность того, что в результате опыта случайная величина примет значение, меньше, чем х, т.е. F(x)=P{X < х}.  Рассмотрим свойства функции F(x).

1. F(-∞)=lim_(x→-∞)F(x)=0. Действительно, по определению, F(-∞)=P{X < -∞}. Событие (X < -∞) является невозможным событием: F(-∞)=P{X < - ∞}=p{V}=0.

2. F(∞)=lim_(x→∞)F(x)=1, так как по определению, F(∞)=P{X < ∞}. Событие Х < ∞ является достоверным событием. Следовательно, F(∞)=P{X < ∞}=p{U}=1.

3. Вероятность того, что случайная величина примет значение из интервала [Α Β] равна приращению функции распределения вероятностей на этом интервале. P{Α ≤X<Β}=F(Β)-F(Α).

4. F(x₂)≥ F(x₁ ), если x_2, > x₁, т.е. функция распределения вероятностей является неубывающей функцией.

5. Функция распределения вероятностей непрерывна слева. FΨ(x_o-0)=limFΨ(x)=FΨ(x_o) при х→ x_o

Функция распределения дискретной случайной величины

Если  - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

называется распределением дискретной случайной величины.

Функция распределения случайной величины, с таким распределением, имеет вид

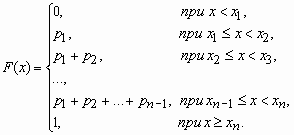
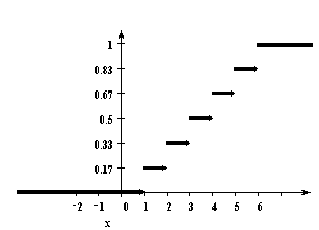
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

2.

Билет 16

1.Математическое ожидание непрерывной случайной величины X, возможные значения которой принадлежат всей оси Ох, определяется равенством: 

Дисперсия непрерывной случайной величины X, возможные значения которой принадлежат всей оси Ох, определяется равенством: 

Случайную величину X называют непрерывной, если ее функция распределения F(X)=P(X < x) непрерывна и имеет производную.  Функция распределения непрерывной случайной величины применяется для вычисления вероятностей попадания случайной величины в заданный промежуток:  P(α < X < β)=F(β) - F(α)  причем для непрерывной случайной величины не имеет значения, включаются в этот промежуток его границы или нет:  P(α < X < β) = P(α ≤ X < β) = P(α ≤ X ≤ β)  Плотностью распределения непрерывной случайной величины называется функция  f(x)=F’(x), производная от функции распределения.

2.

Билет 17

1.Математическим ожиданием (средним значением) случайной величины X, заданной на дискретном вероятностном пространстве, называется число m=M[X]=∑x_ip_i, если ряд сходится абсолютно.

Свойства математического ожидания случайной величины

5. Математическое ожидание постоянной величины равно ей самой: M[C]=C, C – постоянная;

6. M[C•X]=C•M[X]

7. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: M[X+Y]=M[X]+M[Y]

8. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M[X•Y]=M[X]•M[Y], если X и Y независимы.