2.4. Модуляционный метод измерения сдвига фаз Саньяка

Оценка величины Δφ_c по формуле (9) для волоконного контура из световода длиной 1000 м, намотанного на катушку с r = 5 см, при длине волны света λ = 0,85 мкм и угловой скорости вращения 1град/чдает значение Δφ_c = 10^-5 рад. Отсюда следует необходимость разра­ботки чувствительных методов регистрации фазы, обеспечивающих мак­симальное отношение сигнала к шуму (SNR).

Одна из наиболее распространенных схем регистрации связана с применением в контуре ВОГ гармонического фазового модулятора на частоте ω_m и регистрации фазы Саньяка на этой же частоте. Принципиальная схема ВОГ в этом случае отличается от схемы на рис.2.2 установкой на одном из входов в волоконный контур (любом) фазово­го модулятора, изменяющего фазу проходящего излучения по закону:

(20)

Тогда для встречной волны, прошедшей по волоконному контуру, изме­нение фазы будет отставать на время распространения ее в волоконном контуре t₀ = L·n/c (n - показатель преломления световедущей жилы световода), т.е.:

(21)

Величина дополнительного сдвига фаз встречных волн, возникаю­щего в этом случае и входящего дополнительно в аргумент косинуса в формуле (14), равна:

(22)

Выражение (14) для интенсивности излучения тогда принимает вид:

,

где (23)

Соответствующий фототок на выходе фотоприемника с ватт-ампер­ной чувствительностью w равен:

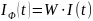(24)

и его значения постоянной составляющей на частотах первой и второй гармоник определяются выражениями (получены разложением (24) по Бесселевым функциям):

(25)

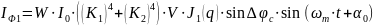(26)

(27)

Здесь J₀ , J₁ , J₂ - функции Бесселя 1-го рода соответствующего порядка.

Из выражений (25) — (27) следует, что регистрация сигнала на первой гармонике частоты модуляции обладает наибольшей чувствитель­ностью при малых угловых скоростях вращения контура. При этом зна­чение аргумента функций Бесселя выбирается равным q = 1,8, что обес­печивает максимум функции J₁ . Для облегчения режима работы моду­лятора величина синуса максимизируется условием ω_m t₀ = π , от­куда для частоты модуляции следует выражение:

(28)

Оценка частоты модуляции при длине световода L = 1 км и n = 1,45 дает величину f_m = 100 кГц. (О других преимуществах выбора такой частоты модуляции будет сказано позднее).

Рис.2.4. Зависимость относительного значения амплитуды первой гармоники фототока от Δφ_c

На рис.2.4 представлена зависимость относительного значения амплитуды первой гармоники фототока от Δφ_c . Эта характеристика нелинейна и имеет синусоидальную форму, однако при малых угловых скоростях с достаточной точностью может аппроксимироваться прямой линией.