16. Условие суммы (дирекционных углов)
В этом ходе возникает условное уравнение дирекционных углов
где невязка
И два условия уравнения координат
,
где невязка
,
В последних двух уравнениях поправки приращений координат следует заменить поправками непосредственно измеренных величин – углов и линий. Заметим, что координатные условные уравнения возникаю также в сети триангуляции.
21 Составить условное уравнение дирекционных углов , если измерены все промежуточные углы, которые близки по величине.
При уравнивании полигонометрических сетей условные уравнения чаще всего составляют для отдельных ходов, входящих в сеть. В каждом ходе возникает три условных уравнения – 2 условных уравнения координат и 1 -уравнение дирекционных углов, которое имеет вид
Где - поправки приближенных значений узловых
направлений, а невязка
Если безошибочны, то поправки равны нулю
25. Метод квадратных корней.
Метод
Гаусса решения системы нормальных
уравнений 
сводится к представлению матрицы R
в виде произведения 
.
При этом получаем две системы уравнений
,
,
где у — преобразованный в схеме Гаусса
вектор b. Искомый вектор
получается в схеме Гаусса по приведенным
ранее формулам. Метод квадратных корней
заключается в представлении матрицы в
виде произведения 
,
где матрицa
.
Имеем
систему уравнений 
(
Z — преобразованный в
схеме решения методом квадратных корней
вектор b). Вектор 
Приведем схему решения системы нормальных
уравнений вида 
методом квадратных корней с попутным
обращением матрицы А.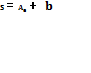 
- суммарный столбец, введенный для
контроля (Вeктор 
Исходя из приведенных выше общих формул,
связанных с решением системы нормальных
уравнений методом квадратных корней,
можно сформулировать следующие правила
вычислений; элементы 
вычисляют последовательно по строкам;
— как корень квадратный из разности
и суммы квадратов всех
расположенных над
;
недиагональный элемент
получают вычитанием из 
суммы произведений элементов t,
взятых из столбцов i и j,
и умножением полученной разности на
;
аналогично вычисляют и элементы 
.
После
вычисления всей строки производят
контроль 
(расхождения между 
и 
)
допускаются в пределах нескольких
единиц последнего удерживаемого знака).
.
Точно так же по столбцу s
по мере получения 
вычисляют величины
и осуществляют контроль 
Отметим, что при числе уравнений k˂10
в элементах
удерживают на 1—2 знака после запятой
больше, чем их имеют элементы 
при
10<к<30 — на 3—4 знака больше. Приведенная
схема вычислений удобна и для обращения
матрицы А. В самом деле, если решение
системы уравнений Ах =b
сводится к последовательному решению
двух систем 
то процесс обращения матрицы А,
заключающийся в решении систем
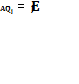(j=1,2,…,k),где
— соответственно j-е
столбцы матриц А и Е, может быть сведен
к решению двух систем 
,
.
Из системы следует, что вектор 
.
Учитывая правило обращения треугольной
матрицы и введя матрицу 
,
столбцами которой служат векторы 
,
напишем
.
Здесь
знаком вопроса обозначены неизвестные
недиагональные элементы матрицы 
.
Из системы следует, что столбцы 
матрицы Q могут быть
получены в схеме решения точно так же,
как и вектор х, если столбец z
последовательно заменить столбцами
.
Элементы матрицы Q удобно
вычислять по строкам, начиная с последней,
как в способе Ганзена. При этом вычисленные
элементы 
i-й строки записывают в
j-й столбец матрицы Q
(в силу ее симметричности), так что в
каждой строке необходимо вычислять
элементы
при i > j
(по этой причине обозначенные знаком
вопроса неизвестные элементы матрицы
вообще не участвуют в вычислениях).
После вычисления элементов каждой
строки осуществляется контроль 
,
где 
-
i-я строка матрицы A(i=j).
Метод квадратных корней, как и метод
Гаусса, может применяться и для систем
уравнений, в которых матрица А не
положительно определена. Может оказаться,
что 
В этом случае приходится прибегать к
мнимым числам, что, однако, не вносит