11

1. Определители второго порядка. Определители третьего порядка

2. Алгебраические дополнения и миноры

3. Система линейных уравнений. Теорема Крамера.

4. Ранг матрицы. Теорема Кронекера – Капелли.

5. Свойства определителей

1. Определители второго порядка

Понятие определителя вводится только для квадратной матрицы.

Определитель – это число, которое считается по определенным правилам. Порядок определителя – это порядок квадратной матрицы. Если для задания матриц использовались круглые скобки, то в теории определителей используют прямые скобки.

Каждой квадратной матрице поставим в соответствие некоторое число, которое будем называть определителем матрицы, и укажем правило его вычисления. Обозначения:

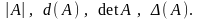
• Дана матрица 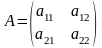. Определителем второго порядка называется число, вычисляемое по правилу:

.

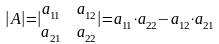Пример 1. .

Определители третьего порядка

• Дана матрица . Определителем третьего порядка называется число, вычисляемое по правилу:

В каждом произведении нет чисел из одного столбца или одной строки. Приведем схему для запоминания порядка получения слагаемых в определителе.

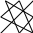
Произведение чисел на одной диагонали берется со знаком «+» (это главная диагональ матрицы), а на другой – с противоположным знаком.

Пример 2.

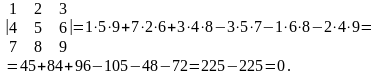
2. Алгебраические дополнения и миноры

Для вычисления определителей порядка больше третьего применяют другие способы вычисления.

• Минором элемента 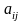определителя называется определитель , полученный из определителя вычеркиванием -ой строки и -го столбца, на пересечении которых стоит элемент .

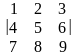Пример 3. Минор определителя есть .

• Алгебраическим дополнением элемента определителя называется минор , умноженный на :

.

Полезно запомнить, что 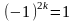и .

Пример 4. В примере 3 алгебраическое дополнение

.

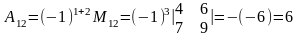3. Метод Крамера (определителей) решения систем линейных уравнений

Правило (метод) Крамера применяется к системам, у которых число уравнений равно числу неизвестных. Этот метод использует определители.

2.1. Число уравнений и неизвестных равно 2

Рассмотрим систему линейных уравнений

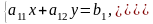
Вычисляются определители:

_, , .

Здесь

- определитель системы, составленный из коэффициентов при неизвестных;

- это определитель, полученный из определителя 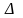заменой столбца коэффициентов при на столбец свободных членов;

- это определитель, полученный из определителя заменой столбца коэффициентов при 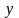на столбец свободных членов.

1. Если , то система совместная и определенная, то есть имеет единственное решение, которое находится по формулам Крамера:

.

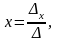
2. Если , а хотя бы один из определителей , отличен от нуля, то система не имеет решений (несовместная).

3. Если , то система имеет бесконечно много решений (совместная и неопределенная).

Пример 1. Решить с помощью метода Крамера систему уравнений

Решение

, поэтому СЛУ имеет единственное решение.

, .

Тогда ; .

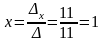Ответ: система уравнений совместна и определенна, ее единственное решение .

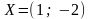Пример 2. Решить с помощью метода Крамера систему уравнений

.

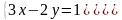Решение

Определитель системы равен ну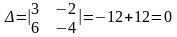лю: , однако один из вспомогательных определителей не равен нулю: , значит, СЛУ не имеет решений, то есть СЛУ несовместная.

Пример 3. Решить с помощью метода Крамера систему уравнений

Решение

, , .

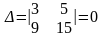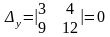Поэтому система имеет бесконечно много решений.

Разделив коэффициенты 2-го уравнения на 3, получим: Оставим только одно из этих уравнений: .

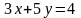Выразим через : , значение - любое действительное число. Это и есть выражение для общего решения СЛУ. Ответ можно записать так: 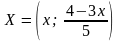, где .

Придавая различные значения, будем получать бесконечное множество частных решений. Например, при получим и первое частное решение . При получим 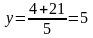и второе частное решение , и так далее.