39

ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАСНПОРТА

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

МОСКОВСКИЙ ГОСУДАСРТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА НИКОЛАЯ II

РОССИЙСКАЯ ОТКРЫТАЯ АКАДЕМИЯ ТРАНСПОРТА

КУРСОВАЯ РАБОТА

По дисциплине: гидрогазодинамика

Вариант № 7

Выполнила студентка:

Шифр:

Рецензент: Кузьминский Р.А.

Москва 2016

Содержание

Введение...................................................................................................................3

Задача № 1................................................................................................................4

Задача № 2..............................................................................................................15

Список литературы................................................................................................32

Приложение............................................................................................................33

Введение

В первой задаче данной курсовой работы необходимо провести гидравлический расчет элементов сложного трубопровода системы водоснабжения при параллельно-разветвленном соединении труб с насосной установкой, а также рассчитать параметры гидравлического удара в трубопроводе, построить пьезометрический график.

Во второй задаче провести газодинамический расчёт сопла Лаваля и определить параметры потока после прямого скачка уплотнения при течении воздуха по трубе.

Задача № 1

Провести гидравлический расчет элементов сложного трубопровода системы водоснабжения при параллельно-разветвленном соединении труб с насосной установкой, а также рассчитать параметры гидравлического удара в трубопроводе.

Исходные данные:

1.1. Горизонтальный трубопровод из стальных труб, схема которого представлена на рис. 1.1, имеет участок с параллельным соединением труб, состоящих из двух линий длиной L₁ и L₂ и диаметром d₁ и d₂. В точках В, С и D заданы расходы воды Q_В, Q_С и Q_D.

Рис. 1.1 Элементы сложного трубопровода системы водоснабжения при параллельно-разветвленном соединении труб

Требуется:

Установить диаметры труб на участках АВ и СД по предельным расходам.

Определить распределение расходов по первой и второй линиям параллельного соединения трубопроводов.

Определить необходимый напор в точке А для обеспечения заданных расходов Q_B, Q_C и Q_D при заданном свободном напоре в конце трубопровода Н_св.

Построить пьезометрическую линию по длине трубопровода.

Исходные данные

Исходные Данные	Номер варианта
	7
LВС1, м	800
LВС2, м	1000
LАВ, м	900
LСD, м	800
D1, мм	100
D2, мм	50
QB, л/с	14
QC, л/с	14
QD, л/с	4
Нсв, м	38

Решение задачи.

1.2 Определяем расчётные расходы на участках:

Q_CD=Q_D = 4 л/с;

Q_BC=Q₁+Q₂=Q_D+Q_C = 4+14 = 18 л/с;

Q_AВ=Q_B+Q_C+Q_D = 14+18+4 = 36 л/с.

1.3. Выбираем диаметры труб D_АВ и D_CD, используя приложение 1.

D_AB = 200мм , D_CD = 100мм.

1.4. Определяем потери напора:

1.5. Потери напора h_CD на участке CD .

Величину h можно определить по формуле

h=1,1S₀Q²L=1,1Q²L/К²,

где S₀ - удельное сопротивление трубы, S₀ = 173 c²/м⁶;

К - расходная характеристика (модуль расхода) труб К = 0,076 м³/с.

Величины S₀ и К для каждого участка можно определить с помощью приложений 2 и 3.

h_СD = 1,1·173·0,000016·800 =2,44м

1.6 Потери напора h_1BC, h_2BC на участке ВС.

Для избежания перетечек из L₁ в L₂ в точке С, необходимо чтобы

h_1ВС=h_2ВС=h_ВС, т.е. S₀₁Q₁²L₁=S₀₂Q₂²L₂.

Отсюда

= ; = ·

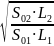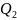
Тогда,

Q_BC=Q₁+Q₂,

= Q₂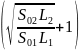

Откуда определяем Q₂, а затем Q₁ и рассчитываем потери напора h_1BC, h_2BC.

Q_BC = Q₂ ,

Q₂ =

где S₀₁ = 173, S₀ = 3686 (см. приложение 8)

Q₂ = = = 2,92л/c

Q₁ =18-2,92 =15,08 л/с

h_1BC = 1,1S₀₁Q₁²L=1,1·173·0,000227·800 = 34,6м;

h_2BC = 1,1S₀₂Q₂²L=1,1·3686·0,000046·1000 = 34,6м

1.7 Потери напора h_АВ на участке АВ.

h_AB = 1,1S_0ABQ_AB²L=1,1·6,96·0,001296·900 = 8,9м

1.8 Определяем необходимый напор в точке А

Н_А=Н_D+h_АВ+h_ВС+h_СD.

Н_А = 38+8,9+34,6+2,44 = 83,94м

1.9 Строим пьезометрическую линию по длине трубопровода с учетом того, что:

Напор в точке А будет равен Н_А = 83,94;

Напор в точке В Н_В=Н_А-h_AB = 83,94 – 8,9 =75,04м;

Напор в точке С Н_С=Н_В-h_ВС = 75,04 – 34,6 =40,44м ;

Напор в точке D Н_D =H_св=Н_С-h_СD = 40,44-2,44= 38м.

Пример построения пьезометрической линии по длине трубопровода представлен на рис. 2.1.

Рис. 2.1 Пьезометрическая линия по длине трубопровода

2.1 Вода при температуре t из водоприемного колодца (рис. 2.1) насосом перекачивается в трубопровод с расходом Q (принимается равным Q_АB по рис. 1.1). Диаметр всасывающей линии насоса - d_вс, длина - L_вс. Ось насоса расположена выше уровня воды в водоприемном колодце на величину Н.

Требуется:

Рассчитать величину вакуума во всасывающей линии водяного насоса, подающего воду в систему трубопровода (Рис. 2.1).

Рис. 2.1 Всасывающая линия водяного насоса

Задачу решить для следующих значений величин:

Исходные данные	Номер варианта
	7
Lвс, м	15
dвс, мм	150
Н, м	1,5
t, °С	15

2.1.Определяем скорость течения в трубе по формуле, V:

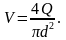
где Q – расход воды в трубопроводе,Q = 36 л/с

d – диаметр трубопровода,м.

V = 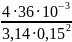= 2,06 м/с

2.2 Определяем потери напора:

При определении потерь напора во всасывающей линии насоса коэффициент местного сопротивления приемного клапана с сеткой берем с таблицы по приложению 4, а колена - принимаем ξ=0,2.

h_м = (ξ_кл + ξ_к)· ,

где ξ_кл – коэффициент местного сопротивления, ξ_м = 7;

ξ_к – коэффициент сопротивления колена_, ξ_к = 0,2

h_м = (7+0,2) = 0,95м

Потерь напора по длине определяем по формуле Дарси-Вейсбаха

,

где λ - коэффициент гидравлического трения (коэффициент Дарси);

L - длина самотечной трубы, м;

d - диаметр трубы, м;

v - скорость течения в трубе, м/с.

Коэффициент трения можем определить по формуле А.Д. Альтшуля

λ= 0,11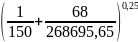 =0,11·(0,007+0,000025)^0,25 = 0,11·0,32=0,0319

где k_э – эквивалентная шероховатости стенок трубопровода (принимаем равным k_э=1 мм);

Re - число Рейнольдса, которое определяем по формуле

R_e = =268695,65

где V –скорость движения жидкости, м/м;

ν - кинематический коэффициент вязкости ν (принимаем по приложению 5) ν= 1,01·10^-6.

Фактическое число Рейнольдса Re сравниваем с его с критическим числом Re_кр.= 2320. При этом, если Re  Re_кр, то режим движения ламинарный, если Re > Re_кр, то режим движения турбулентный.

В нашем случае движение жидкости в трубопроводе турбулентное и коэффициент α = 1.

h_l =0,0319 · = 6,9м

Общие потери напора составят:

h = h_l + h_м = 6,9+0,95 = 7,85м

2.3.Определяем величину вакуума

Искомую величину вакуума при входе в насос определяем из уравнения Бернулли, составленного для сечений 1-1 и 2-2

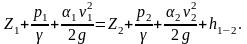
Принимая за горизонтальную плоскость сравнения сечение 1-1, т.е. Z₁=0, Z₂=Н и считая v₁=0, а также учитывая, что давление в сечении 1-1 равны атмосферному (Р₁=Р_АТ), имеем расчетный вид уравнения

или

Величину вакуума в сечении 2-2 определяем из выражения

Н_дейст. = Н + + h_1-2,

где Н_дейст. = - величина вакуума, м;

Н – высота всасывания, м;

α –коэффициент режима движения жидкости в трубопроводе, α = 1;

V₂ – скорость движения жидкости, м/с.

Н_дейст. = 1,5+ + 7,85 = 9,6м

Ответ. Величина вакуума во всасывающей линии водяного насоса, подающего воду в систему трубопроводов составит 9,6м.

3.1 По стальному трубопроводу длиной L, диаметром d и толщиной стенок δ перекачивается вода с расходом Q (рис. 1.3).

Требуется:

1. Определить повышение давления в трубопроводе, если время закрывания задвижки равно Т_з.

2. Найти максимально допустимое давление для данного трубопровода, если допустимое напряжение стенок на разрыв σ_доп=50 МПа.

3. Исходя из максимально допустимого повышения давления, определить минимально допустимое время закрытия задвижки.

Рис. 1.3 Схема водопровода с вентилем

Задачу решить для следующих значений величин:

Исходные данные	Номер варианта
	7
d, мм	350
δ, мм	7,5
Q, л/с	140
L, м	1800
Тз, с	2

Определяем величину Т - промежутка времени  когда вся жидкость в трубе остановится и скорость будет равна нулю по формуле:

где L – длина трубопровода;

с - скорость распространения ударной волны, которая для случая движения воды в стальном трубопроводе вычисляется по формуле:

где d – диаметр трубопровода;

δ - толщина стенок трубы.

с = = 1177 м/с

Т = = 3,06с

Определяем повышение давления в трубопроводе по формулам:

при прямом ударе

при непрямом ударе

Различают полный или прямой и неполный или непрямой гидравлический удар.

Если время закрывания крана или задвижки Т_з меньше фазы удара Т, то возникает прямой удар. Т_з<Т

Если время закрытия задвижки больше фазы удара – непрямой удар. Т_з˃Т

В нашем случае Т₃ больше фазы удара Т - значит у нас непрямой удар. Значит величину повышения давления будем определять по формуле

Δp =ρvc

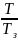
где ρ - плотность жидкости;

v - скорость движения потока до закрытия задвижки;

с - скорость распространения ударной волны;

Т - фаза ударной волны;

Т_з - время закрывания задвижки.

Определяем скорость течения жидкости в трубе по формуле:

где Q – расход воды в трубопроводе, л/с

d – диаметр трубопровода, м.

V = = 1,5м/с

Δp = 1000·1177·1,5 = 2,7·10⁶Па

Максимально допустимое давление для данного трубопровода определяется с учетом допустимого напряжения стенок на разрыв σ_доп.

Разрывающее усилие, испытываемое стенками трубопровода под влиянием давления р, определяем по формуле

F=pdL.

Это усилие воспринимается площадью сечения стенок трубопровода

а растягивающее напряжение

Отсюда искомое максимально допустимое давление для заданного трубопровода определяем по формуле

где - допустимое растягивающее напряжение = 20МПа по условии задачи;

d – диаметр трубопровода;

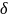- толщина стенки трубопровода.

Р_макс. = 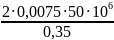= 2,14·10⁶ Па

Минимально допустимое время закрывания задвижки определяем по формуле

Т_з.мин. =

где ρ- плотность жидкости;

v – скорость жидкости в трубопроводе до закрытия крана;

с - скорость распространения ударной волны;

Т – время остановки потока при закрытии крана;

Р_макс. – максимально допустимое давление в трубопроводе.

Т_з.мин. = = 2,5с

Ответ. ΔР= 2,7·10⁶Па, Р_макс.=2,14·10⁶Па, Т_з.мин.= 2,5с

Задача № 2

2.1. Выполнить газодинамический расчёт сопла Лаваля.

Исходные данные:

Провести газодинамический расчёт сопла Лаваля (Рис. 1.4), обеспечивающего в расчётном режиме массовый расход кислорода G. Параметры торможения: Р₀; Т₀. Скорость входа газа w_ВХ, показатель адиабаты k=1,41. Углы раствора сопла: дозвуковой части α=80º; сверхзвуковой части β=65º. Давление на срезе сопла р₂ .

Требуется:

Определить, параметры газа в основных (входного, критического и выходного) и дополнительных сечениях 1, 2, 3, 4 и построить графики зависимости Р, T, W, a, ρ по длине сопла.

Рис. 2,1 Сопло Лаваля

Задачу решить для следующих значений величин:

Величина	Варианты
	7
G, кг/с	15,0
Р0, МПа	10.0
Т0, °К	750
wВХ, м/с	175
р2, МПа	0,0004

По мере движения газа по соплу (рис.2.1), его абсолютная температура Т и давление Р снижаются, а скорость w возрастает (рис. 2.2).

Рис. 2.2. График изменения абсолютной температуры, давления и скорости потока

Скорость газа в узком сечении определя­ется по уравнению

а на выходе из сопла по уравнению

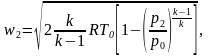
в котором р₂=р_н.

Максимальная скорость на выходе из сопла Лаваля достигается при истечении в абсолютный вакуум, когда р_н/р₂=0.

Массовый расход газа G через сопло Лаваля определяется по уравнению

При этом принимаются параметры либо в критическом (узком) сечении, либо в выходном сечении сопла. При определнии G по параметрам узкого сечения принимаются ω=ω_кр, р=р_кр=p₀β_кр, а параметрам выходного сечения ω=ω₂, р=р₂=р_н (здесь р_н – давление на срезе сопла).

Макси­мальный расход газа ограничивается узким сечением сопла, когда скорость в нем равна скорости звука и β=β_кр, (р/р₀=р_кр/р₀).

Так как при β<β_кр в узком сечении р/р₀=р_кр/р₀=const, то и массовый расход газа остается неизменным, равным максимальному.