4.Алгебраическая и тригонометрическая формы комплексных чисел Алгебраическая форма комплексного числа

Алгебраической формой комплексного числа называется запись комплексного числа z в виде z=x+iy, где x и y  – действительные числа, i– мнимая единица.

Тригонометрическая форма комплексного числа

Тригонометрической формой комплексного числа z=x+iy, не равного нулю, называется запись z=r(cosα+isinα) где r=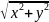 — модуль комплексного числа z.

Задание. Записать число   в тригонометрической форме.

Решение. Для получения тригонометрической формы заданного комплексного числа найдем вначале его модуль и аргумент. Так как  ,  , то

Тогда тригонометрическая форма заданного числа   имеет вид:

Ответ. 

5.Формула Муафра. Извлечение корня

Корнем  -ой степени из комплексного числа   называется такое комплексное число  ,  -я степень которого равна  , то есть

Корень  -ой степени из комплексного числа   обозначается символом   и на множестве комплексных чисел имеет ровно   значений.

Если комплексное число   задано в тригонометрической форме:  , то все значения корня  -ой степени вычисляются по формуле Муавра (Абрахам де Муавр (1667 - 1754) - английский математик):

Геометрически все значения корня лежат на окружности радиуса   с центром в начале координат и образуют правильный  -угольник.

Задание. Вычислить корень четвертой степени из 

Решение. Запишем заданное число в тригонометрической форме, для этого вычислим модуль и аргумент:

То есть

Тогда

Отсюда все значения корня:

Покажем, что все значения корня лежат на окружности радиуса   и образуют правильный четырехугольник, то есть квадрат (рис. 1):

Ответ. 

 

6. Кольцо многочленов от одной переменной

Пусть   — ассоциативное коммутативное кольцо с единицей. Рассмотрим множество бесконечных упорядоченных последовательностей  ,  , в которых почти все элементы, кроме конечного числа, равны нулю. Две последовательности будем складывать по правилу:

.

Умножение зададим формулой

, где  .

Предложение 1. Построенное множество с указанными операциями сложения и умножения является ассоциативным коммутативным кольцом с единицей. Нулевым элементом является нулевая последовательность  , противоположным элементом для   — элемент  , единичным элементом —  .

Последовательности   при сложении и умножении ведут себя так же, как элементы   кольца  , поэтому вместо   будем писать  .

Обозначим

.

Тогда по правилу умножения последовательностей получим

… … …

.

И в новых обозначениях последовательность   запишется в виде  .

Определение 1. Построенное кольцо будем обозначать через   и называть кольцом многочленов от одной переменной¹⁾, а его элемент   — многочленом²⁾.

Определение 2. Элементы   многочлена   называются коэффициентами³⁾ многочлена  .

Определение 3. Многочлен, все коэффициенты которого равны нулю, называется нулевым⁴⁾.

Замечание 1. Кольцо   также называют алгеброй многочленов от одной переменной, имея ввиду, что определено умножение многочлена   на скаляр   по формуле

,

а значит,   является алгеброй над кольцом  .

Формулировка теоремы Безу

Теорема

Остаток от деления многочлена   на двучлен   равен   .

Следствия из теоремы Безу

1. Число   - корень многочлена   тогда и только тогда, когда   делится без остатка на двучлен   .

Отсюда, в частности, следует, что множество корней многочлена   тождественно множеству корней соответствующего уравнения   .

2. Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).

3. Пусть   - целый корень приведенного многочлена   с целыми коэффициентами. Тогда для любого целого  число   делится на   .

Теорема Безу дает возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого уже на единицу меньше: если  , то заданный многочлен   можно представить в виде:

Таким образом, один корень найден и далее находятся уже корни многочлена  , степень которого на единицу меньше степени исходного многочлена. Иногда этим приемом - он называется понижением степени - можно найти все корни заданного многочлена.

Примеры решения задач

Пример

Задание. Найти остаток от деления многочлена   на двучлен 

Решение. Согласно теореме Безу искомый остаток равен значению многочлена в точке   . Найдем тогда  , для этого значение   подставим в выражение для многочлена   вместо   . Будем иметь:

Ответ. Остаток равен 5