МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ОДЕСЬКИЙ ДЕРЖАВНИЙ АГРАРНИЙ УНІВЕРСИТЕТ
ІНЖЕНЕРНИЙ ФАКУЛЬТЕТ
КАФЕДРА ГЕОДЕЗІЇ ТА ПРИРОДОКОРИСТУВАННЯ
Контрольна робота з дисципліни « математична обробка геодезичних вимірів »
Студента 2 курсу 3В
6.080101 „Геодезія, |
-
картографія та землеустрій”
Перевірив: доц. Малащук О.С.
М. Одеса – 2016 рік
Завдання №1. Математична обробка рівноточних вимірів
В таблиці
наведені результати рівноточних вимірів.
Обчислити середнє арифметичне і оцінити
його на точність (
,
mΔ,
МΔ
).
Вихідні дані
№ |
Таблиця випадкових чисел нормального закону розподілу (свій варіант) |
1. |
2,376 |
2. |
0,205 |
3. |
-0,465 |
4. |
-0,111 |
5. |
0,696 |
6. |
-0,541 |
7. |
0,159 |
8. |
-0,577 |
9. |
-0,854 |
10. |
0,238 |
11. |
-0,655 |
12. |
-0,021 |
13. |
-0,600 |
14. |
0,173 |
15. |
0,031 |
Варіанти додаються.
Розв’язання:
Вибирають х0 ( деяке наближене число виміряної величини, яке вибирається з таким розрахунком, щоб усі відхилення εі були малими числами, бажано додатними ), в нашому випадку х0 = 3,0000.
Тоді розраховуємо εі за формулою:
εі = хі – х0
εі – відхилення виміряної величини від х0 ; хі – виміряна величина.
Результати заносимо в п’ятий стовпчик таблиці 1.
Таблиця 1. Схема рішення
№ |
Варіант свій |
Вихідні дані |
Результат виміру, хі |
Залишок, εі |
ε2і |
Відхилення, vі |
v2і |
1 |
2 |
3 |
4=2+3 |
5 |
6 |
7 |
8 |
1. |
2,376 |
4,5111 |
6,8871 |
3,8871 |
15,10954641 |
-2,2630 |
5,121169 |
2. |
0,205 |
4,5114 |
4,7164 |
1,7164 |
2,94602896 |
-0,0923 |
0,00851929 |
3. |
-0,465 |
4,5125 |
4,0475 |
1,0475 |
1,09725625 |
0,5766 |
0,33246756 |
4. |
-0,111 |
4,5126 |
4,4016 |
1,4016 |
1,96448256 |
0,2225 |
0,04950625 |
5. |
0,696 |
4,5126 |
5,2086 |
2,2086 |
4,87791396 |
-0,5845 |
0,34164025 |
6. |
-0,541 |
4,5125 |
3,9715 |
0,9715 |
0,94381225 |
0,6526 |
0,42588676 |
7. |
0,159 |
4,5116 |
4,6706 |
1,6706 |
2,79090436 |
-0,0465 |
0,00216225 |
8. |
-0,577 |
4,5112 |
3,9342 |
0,9342 |
0,87272964 |
0,6899 |
0,47596201 |
9. |
-0,854 |
4,5099 |
3,6559 |
0,6559 |
0,43020481 |
0,9682 |
0,93741124 |
10. |
0,238 |
4,5092 |
4,7472 |
1,7472 |
3,05270784 |
-0,1231 |
0,01515361 |
|
|
|
х0 = 3,0000 = 4,62406
Δ0 = 0,00004 |
[εі] =16,2406 |
[ε2і] = 34,08558704 |
[vі] = 0,0004 |
[v2і] = 7,70987822 |
=
4,6241
2. Вираховуємо середнє арифметичне виміряної величини:
= х0 + [εі] / n = 3,0000 + 16,2406 ÷ 10 = 4,62406.
[εі] – сума відхилень; n – кількість вимірів.
Округлюють одержане значення середнього арифметичного до одержуваного десятинного знаку і визначають помилку округлення: = 4,6241.
Далі визначають помилку округлення ( Δ0 ) за формулою:
Δ0 = – = 4,6241 – 4,62406 = 0,00004.
3. Обчислюють величину відхилення ( vі ) виміряних величин відносно округленого середнього арифметичного:
vі = – хі
Дані заносимо в стовпчик 7 таблиці №1.
4. Здійснюють контроль правильності обчислень округленого значення середнього арифметичного. Якщо воно правильне, то виконується рівність:
[vі] = Δ0 х n ; 0,00004 = 0,0004 х 10 → 0,00004.
5. Обчислюємо параметри величин: ε2і і заносимо їх в стовпчик 6 таблиці №1, v2і і заносимо їх в стовпчик 8 таблиці №1. Далі визначаємо суми: [ε2і], [v2і], [εі] 2:
[ε2і] = 34,08558704; [v2і] = 7,70987822; [εі] 2 = 263,7570884.
6. Здійснюємо контроль правильності обчислень v2і :
[v2і] = [ε2і] – [εі] 2 / n;
7,70987822 = 34,08558704 – 263,7570884 ÷ 10 → 7,709878204.
7,70987822 ≈ 7,709878204.
7. Визначають середню квадратичну похибку одного виміру:
та точність її
визначення:
10. Визначають середню квадратичну похибку середнього арифметичного:
та точність її
визначення:
11. Записують
кінцевий результат:
;
4,3311 ≤ 4,6241≤ 4,9171.
ЗАВДАННЯ №2 Математична обробка нерівноточних вимірів
Відмітка Н точки місцевості одержана по шести нівелірним рейкам. Провести математичну обробку результатів вимірів по даних, приведених в таблиці, якщо ваги окремих вимірів:
р = N / m2. N = 15 - свій
N - номер варіанту
Розв’язання:
1. Відповідно до рекомендації по умові задачі визначаємо ваги вимірів і заносимо в стовпчик 6 таблиці №1. Вираховуємо їх суму: [р] = 11,495.
2. Вибирають х0 ( деяке наближене число виміряної величини, яке вибирається з таким розрахунком, щоб усі відхилення εі були малими числами, бажано додатними ), в нашому випадку х0 = 195,000.
Тоді розраховуємо εі за формулою:
εі = хі – х0
εі – відхилення виміряної величини від х0 ; хі – виміряна величина.
Результати заносимо в стовпчик 7 таблиці №1.
3. Визначаємо добутки р х εі і заносимо їх в стовпчик 8 таблиці №1, та добутки р х ε2і і заносимо їх в стовпчик 9. Далі визначаємо їх суми:
[ р х εі] = 21,457763 ; [ р х ε2і ] = 53,36994271.
4. Вираховуємо середнє вагове виміряної величини:
= х0 + [ р х εі] / [р] = 195,000 + 21,457763 ÷ 11,495 = 196,866704045.
Округлюють одержане значення середнього вагового до одержуваного десятинного знаку і визначають помилку округлення: = 196,867.
Далі визначають помилку округлення ( Δ0 ) за формулою:
Δ0 = – = 196,867 – 196,866704045 = 0,000295954.
3. Обчислюють величину відхилення ( vі ) виміряних величин відносно округленого середнього вагового:
vі = – хі
Дані заносимо в стовпчик 10 таблиці №1.
4. Здійснюють контроль правильності обчислень округленого значення середнього арифметичного. Якщо воно правильне, то виконується рівність:
[р х vі] = Δ0 х [р] ;
0,003402 = 0,000295954 х 11,495 → 0,003401999;
0,003402 ≈ 0,003401999
5. Обчислюємо параметри величин р х vі - і заносимо їх в стовпчик 11, р х v2і - і заносимо їх в стовпчик 12.
Далі визначаємо суми: [ р х vі ] та [ р х v2і]:
[ р х vі ] = 0,003402; [ р х v2і] = 13,31465072.
6. Здійснюємо контроль правильності обчислень р х v2і:
[ р х v2і] = [ р х ε2і] – [ р х εі] 2 / [р];
13,31465072 = 53,36994271 – 460,435593 ÷ 11,495 → 13,31464971;
13,31465072 ≈ 13,31464971.
7. Знаходять помилку одиниці ваги та її точність:
=
=
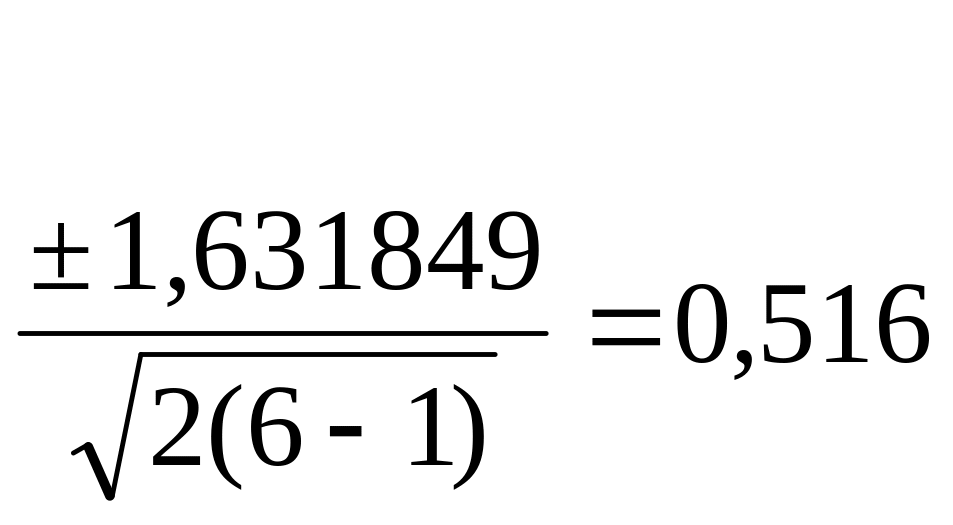
Де: mµ – середня квадратична похибка визначення .
Знаходять середню квадратичну похибку середнього вагового, та її точність.
Де: Mm – середня квадратична похибка визначення M.
Записують кінцевий результат:
(
).
196,386 ≤ 196,867 ≤ 197,348.
Таблиця 7. Схема рішення
№ |
Варіант свій |
Вихідні дані |
Результат виміру, хі |
m2 |
р |
εі |
р х εі |
р х ε2і |
vі |
р х vі
|
р х v2і |
1 |
2 |
3 |
4 =2+3 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1. |
2,376 |
196,529 |
198,905 |
6,3 |
2,381 |
3,905 |
9,297805 |
36,30792853 |
-2,038 |
-4,852478 |
9,889350164 |
2. |
0,205 |
196,522 |
196,727 |
8,4 |
1,786 |
1,727 |
3,084422 |
5,326796794 |
0,140 |
0,25004 |
0,0350056 |
3. |
-0,465 |
196,517 |
196,052 |
9,1 |
1,648 |
1,052 |
1,733696 |
1,823848192 |
0,815 |
1,34312 |
1,0946428 |
4. |
-0,111 |
196,532 |
196,421 |
4,3 |
3,488 |
1,421 |
4,956448 |
7,043112608 |
0,446 |
1,555648 |
0,693819008 |
5. |
0,696 |
196,530 |
197,226 |
5,2 |
0,192 |
2,226 |
0,427392 |
0,951374592 |
-0,359 |
-0,068928 |
0,024745152 |
6. |
-0,541 |
196,520 |
195,979 |
7,5 |
2,000 |
0,979 |
1,958 |
1,916882 |
0,888 |
1,776 |
1,577088 |
|
|
|
х0 = 195,000 =196,866704045 = 196,867 Δ0 = 0,000295954 |
|
[р] = 11,495 |
|
[ р х εі] = 21,457763 |
[ р х ε2і ] = 53,36994271 |
|
[ р х vі] = 0,003402
|
[ р х v2і] = 13,31465072 |
Варіант №___
Вихідні дані
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
tі |
-2,184 |
-0,040 |
0,298 |
-0,093 |
0,509 |
0,142 |
0,836 |
-0,144 |
-0,671 |
-0,209 |
№ |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
tі |
-0,234 |
-0,399 |
0,659 |
0,124 |
0,469 |
-0,335 |
-0,661 |
-0,148 |
-0,819 |
0,985 |
Задача №3 Врівноважити кути геодезичного чотирикутника.
№ |
Вихідні кути |
Значення випадкових чисел нормального закону розподілу ( tі, в секундах ) свій варіант |
Кінцеві значення кутів |
1. |
28˚59′38″ |
-2,184 |
28˚59′35,816″ |
2. |
47˚02′04″ |
-0,040 |
47˚02′03,960″ |
3. |
66˚34′59″ |
0,298 |
66˚34′59,298″ |
4. |
37˚23′20″ |
-0,093 |
37˚23′19,907″ |
5. |
29˚22′38″ |
0,509 |
29˚22′38,509″ |
6. |
46˚39′14″ |
0,142 |
46˚39′14,142″ |
7. |
65˚54′49″ |
0,836 |
65˚54′49,836″ |
8. |
38˚03′34″ |
-0,144 |
38˚03′33,856″ |
Таблиця 1. Вихідні дані