
- •Суммарные, средние и предельные величины в экономике.
- •Необходимое условие экстремума.
- •3. Модели функций спроса и предложения.
- •4. Стандартная и каноническая формы злп.
- •3.Каноническая, или основная, форма записи:
- •5. Графический метод решения злп.
- •Графический способ решения задачи линейного прогаммированя
- •6. Взаимно-двойственные злп и их экономический смысл.
- •6. Взаимно-двойственные злп и их экономический смысл.
- •2.1. Определение и экономический смысл двойственной злп
- •6.1. Экономическая интерпретация задачи, двойственной задаче об использовании ресурсов
- •7. Теоремы двойственности и их экономический смысл.
- •7.Двойственность в линейном программировании. Связь между двойственными задачами. Основные теоремы двойственности и их экономический смысл.
- •Симплекс метод решения злп (схема).
- •10. Постановка транспортной задачи. Нахождение опорного решения методом минимальной стоимости.
- •23. Изокванты производственной функции Кобба-Дугласа.
- •24. Производственная функция Кобба-Дугласа.
- •25. Решение, оптимальное по Парето (на примере)
- •27. Производственная функция и ее экономико-математические свойства.
- •28. Достаточные условия экстремума фнп (по угловым минорам).
- •1) Необходимое условие экстремума.
- •29. Критерий Сильвестра знакоопределенности квадратичной формы.
- •30. Предельная норма замещения одного товара другим.
- •31. Производственная функция Кобба - Дугласа.
Симплекс метод решения злп (схема).

10. Постановка транспортной задачи. Нахождение опорного решения методом минимальной стоимости.
Транспортная задача. Метод минимальной стоимости
22.12.2011, 12:50 |
Метод минимальной стоимости прост и позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи C=(cij).
Как
и метод северо-западного угла, он
состоит из ряда однотипных шагов, на
каждом из которых заполняется только
одна клетка таблицы, соответствующая
минимальной стоимости:
Пример 38.2 Используя метод минимальной стоимости построить начальное опорное решение транспортной задачи.
Решение:
1.
Запишем отдельно матрицу стоимостей
для того, чтобы было удобнее выбирать
минимальные стоимости.
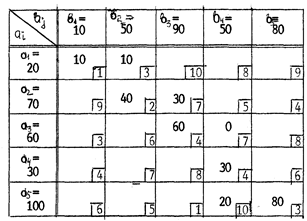
2. Среди элементов матрицы стоимостей выбираем наименьшую стоимость C11=1, отмечаем ее кружочком. Данная стоимость имеет место при перевозке груза от 1-го поставщика 1-му потребителю. В соответствующую клетку записываем максимально возможный объем перевозки: x11 = min {a1; b1} = min {60; 40} =40 т.е. минимум между запасами 1-го поставщика и запросами 1-го потребителя. 2.1. Запасы 1-го поставщика уменьшаем на 40. 2.2. Исключаем из рассмотрения 1-го потребителя, так как его запросы полностью удовлетворены. В матрице C вычеркиваем 1-ый столбец. 3. В оставшейся части матрицы C минимальной стоимостью является стоимость C14=2. Максимально возможная перевозка, которую можно осуществить от 1-го поставщика 4-му потребителю равна x14 = min {a1'; b4} = min {20; 60} = 20, где a1 со штрихом это оставшиеся запасы первого поставщика. 3.1. Запасы 1-го поставщика исчерпаны, поэтому исключаем его из рассмотрения. 3.2. Запросы 4-го потребителя уменьшаем на 20. 4. В оставшейся части матрицы С минимальная стоимость C24=C32=3. Заполняем одну из двух клеток таблицы (2,4) или (3,2). Пусть в клетку запишем x24 = min {a2; b4} = min {80; 40} =40 . 4.1. Запросы 4-го потребителя удовлетворены. Исключаем его из рассмотрения вычеркивая 4-й столбец в матрице C. 4.2. Уменьшаем запасы 2-го поставщика 80-40=40. 5. В оставшейся части матрицы C минимальная стоимость C32=3. Запишем в клетку (3,2) таблицы перевозку x32 = min {a3; b2} = min {100; 60} =60. 5.1. Исключим из рассмотрения 2-го потребителя. Из матрицы C исключаем 2-ой столбец. 5.2. Уменьшим запасы 3-го поставщика 100-60=40 6. В оставшейся части матрицы C минимальная стоимость C33=6. Запишем в клетку (3,3) таблицы перевозку x33 = min {a3'; b3} = min {40; 80} =40 6.1. Исключим из рассмотрения 3-го поставщика, а из матрицы C 3-ю строку. 6.2. Определяем оставшиеся запросы 3-го потребителя 80-40=40. 7. В матрице C остался единственный элемент C23=8. Записываем в клетку таблицы (2,3) перевозку X23=40. 8. Проверяем правильность построения опорного решения. Число занятых клеток таблицы равно N=m+n — 1=3+4 -1. Методом вычеркивания проверяем линейную независимость векторов-условий, соответствующих положительным координатам решения. Порядок вычеркивания показан на матрице X:
Вывод: Решение методом минимальной стоимости (таблица 38.3) является "вычеркиваемым" и, следовательно опорным. |
|
|
|
|
Пример.
1. Проверим, является ли данная задача замкнутой. Подсчитаем суммарные запасы груза и суммарные потребности заказчиков
Поскольку 2. Построим первый опорный план транспортной задачи методом северо-западного угла. Начинаем заполнение распределительной таблицы с верхней левой клетки, то есть построение исходного опорного плана начинаем с удовлетворения потребностей первого потребителя b1 за счет запасов первого поставщика a1. Для этого сравниваем запас a1 = 200 с потребностями b1 = 150. Так как a1 > b1, то потребности b1 полностью удовлетворяем за счет a1, и в первую клетку помещаем min (200, 150)=150. У первого поставщика осталось 50 единиц груза. Так как потребности первого получателя груза полностью удовлетворены, исключим из рассмотрения первый столбец, заполнив в нем оставшиеся клетки точками. Далее заполняем таблицу по строкам слева направо и сверху вниз. Следующая самая верхняя левая незаполненная клетка – (1,2). Потребителю b2 поставляем 50 единиц груза, оставшихся у первого поставщика. Поскольку от первого поставщика весь груз вывезен, заполняем оставшиеся клетки первой строки точками. Второму получателю, пока что, недопоставлено 80 единиц груза. Следующая незаполненная клетка – (2,2). Потребителю b2 отправляем недостающие 80 единиц груза, при этом его потребности полностью удовлетворены, поэтому оставшиеся клетки во втором столбце заполняем точками. У второго поставщика a2 осталось еще 100 единиц груза. Аналогичным образом заполняем оставшиеся клетки, пока не удовлетворим всех потребителей и не вывезем все запасы груза у поставщиков.
В результате распределения груза получим первый опорный план, в котором x11 = 150, x12 = 50, x22 = 80, x23 = 100, x33 = 50, x34 = 140. Эти переменные соответствуют заполненным клеткам и являются базисными, остальные переменные, соответствующие клеткам с точками, являются свободными (значения свободных переменных равны нулю). Первый опорный план можно представить в матричном виде
Число заполненных клеток k = 6. Это число должно равняться рангу системы ограничений r = m + n – 1 = 3 + 4 – 1 = 6. Так как k = r = 6, то построенный план является невырожденным. Подсчитаем затраты на перевозку по этому плану
3. Построим первое опорное решение транспортной задачи методом минимальной стоимости (минимального тарифа).
Найдем клетку с минимальным тарифом. Это клетка (1,3) с тарифом C13 =1. Построение исходного опорного плана начинаем с занесения поставки груза в клетку с наименьшей стоимостью c13. Заполняем клетку x13 = 150. Оставшиеся клетки третьего столбца заполняем точками, так как потребности третьего получателя полностью удовлетворены. У первого поставщика осталось 50 единиц груза. Ищем следующую клетку с минимальным тарифом. Таких клеток две: c14 =2, c32 =2. Заполним сначала клетку (3,2). Поставим в нее x32=min (190, 130)=130. Второй столбец заполняем точками. У третьего поставщика осталось 60 единиц груза. Ищем следующую клетку с наименьшим тарифом – это клетка (1,4). В нее помещаем 50 единиц груза, min(50,140)=50. Первую строку заполняем точками, так как от первого поставщика вывезен весь груз. Четвертому получателю недопоставлено 90 единиц. Аналогичным образом распределяем весь имеющийся груз и получаем первый опорный план перевозок.
Подсчитаем затраты на перевозку по этому плану.
Итак, в каждой строке и в каждом столбце таблицы заполнена хотя бы одна клетка, циклов по заполненным клеткам нет, число заполненных клеток m+n-1=6, следовательно, план опорный и невырожденный. 4. Проверка первого опорного плана (решения) на оптимальность. Метод потенциалов
После
построения исходного опорного плана
приступаем к проверке его на оптимальность
методом потенциалов, который заключается
в последовательном улучшении опорных
планов транспортной задачи на основе
информации, полученной с помощью
чисел, называемых потенциалы
поставщиков В таблице в дополнительном столбце справа помещаем потенциалы отправителей , а в строке снизу – потенциалы получателей. Составим систему уравнений для определения потенциалов:
Из этой системы находим
Считаем оценки для свободных клеток:
Запишем получившиеся оценки в левом верхнем углу свободных клеток.
Так
как среди оценок
Сроим
цикл пересчета, начиная с клетки (3,3),
в которую нужно поместить поставку
груза (её отмечают знаком «+»), и двигаясь
по занятым клеткам (в данном случае
это клетки (3,4), (1,4), (1,3)), поочередно
отмечая их знаками «-», «+». Если в
клетку (3,3) добавили +
Определяем
величину поставки
в
клетку (3,3), как минимальную величину
из поставок, стоящих в отрицательных
клетках, то есть В результате получаем новое опорное решение или новый опорный план, в котором клетки с грузом, равным величине , становятся свободными.
Если
освобождается больше одной клетки,
то есть число заполненных клеток
меньше числа m + n - 1, то такой план
называется вырожденными, и для
определения потенциалов необходимо
ввести недостающее количество нулевых
элементов в число основных базисных
переменных. Свободные клетки заполняют
нулевыми поставками так, чтобы они не
образовывали цикл по заполненным
клеткам, и чтобы в каждой строке и в
каждом столбце находилась хотя бы
одна заполненная клетка. Проверим
новый опорный план на оптимальность.
Пусть
Число
заполненных клеток k=m+n-1, следовательно,
план невырожденный. Найдем оценки
Возьмем клетку (2,2) за начало цикла пересчета. Цикл будет проходить по клеткам (2,2), (3,2), (3,3), (1,3), (1,4), (2,4) и опять вернется в (2,2).
Ищем
количество единиц груза
Проверяем данный опорный план на оптимальность
Полученный опорный план является оптимальным, так как все оценки для свободных клеток . Выписываем оптимальный план: x11 = 0; x12 = 0; x13 = 60; x14 =140; x21 = 150; x22 = 30; x23 = 0; x24 = 0; x31 = 0; x32 = 100; x33 = 90; x34 = 0. Или в матричной форме
Высчитываем минимальные затраты на транспортировку продукции:
12. Постановка транспортной задачи. Нахождение опорного решения методом северо-западного угла. Сущность метода поясним на примере решения (табл. 8.2.1). Метод северо-западного угла Таблица 8.2.1
Z1 = 1130 Процесс распределения ресурсов начинается с клетки, расположенной на «северо-западе», то есть в левом верхнем углу. Ей соответствует ресурс а1 = 20 и
потребность b1 = 10. Удовлетворяем потребность полностью, остаётся ресурс, равный 10. Теперь, по правилу, “дораспределяем» остаток ресурса, передав его следующей потребности b2 которая его забирает, но с нехваткой относительно её потребности. Нехватка ресурса для потребности b2 восполняется уже за счёт ресурса a2 ,расположенного, уже, во второй строчке таблицы. Действия повторяются таким же образом и далее, с образованием ряда ступенек, ведущих в правый нижний угол, где и заканчивается процесс начального распределения. При нахождении опорного решения данным образом следует иметь в виду, что иногда на некоторой клетке таблицы одновременно заканчиваются и ресурсы, и потребности. Тогда для дальнейшего продвижения (по правилам расчёта) записывается базисный ноль -либо в последующей клетке той же строчки, либо в последующей клеточке того же столбца. В законченном расчёте любого опорного решения количество заполненных клеток должно быть равно рангу системы минус единица. В противном случае, реализация алгоритма нахождения опорного решения становится невозможной. Как первое, так и все последующие решения являются возможными для практического осуществления, а эффективность каждого оценивается значением целевой функции.Целевая функция практически служит критерием эффективности того или иного плана, записанного в виде корреспонденций груза в каждой клеточке распределительной таблицы.
13. Решение транспортной задачи сведением ее к стандартной ЗЛП. Стандартная и каноническая формы задачи линейного программирования Обратите внимание на то, что в указанных выше двух примерах задачи имели достаточно разный вид: в задаче о диете требовалось найти минимум целевой функции, а в задаче о плане производства - максимум. В задаче о диете ограничения имели вид
а в задаче о плане производства - вид
Такой разнобой неудобен при разработке алгоритмов решения этих задач. Поэтому имеются некоторые стандартные формы задач линейного программирования, к которым и приводят различные конкретные задачи. Прежде чем выписывать эти формы, договоримс я об обозначениях. Для более краткой записи мы будем использовать векторную или матричную запись. Подвекторами мы будем понимать вектора-столбцы, например
Первая стандартная форма задачи линейного программирования имеет вид
Введем вектора
a также вектора
и матрицу
Заметим, что
комбинация
Можно использовать и матричные обозначения. Тогда комбинация
Вторая стандартная форма задачи линейного программирования имеет вид
В векторной форме эта задача имеет вид
и в матричной форме - вид
Канонической формой задачи линейного программирования называется задача вида
В векторной форме эта задача имеет вид
и в матричной форме - вид
Во всех этих
задачах функцию
называют целевой
функцией. Вектор
Любой набор
чисел 14. Нахождение опорного решения транспортной задачи методом минимальной стоимости. Транспортная задача. Метод минимальной стоимости
15. Задача дробно-линейного программирования на примере максимизации рентабельности. Дробно-линейное программирование
Дробно-линейное
программирование относится к нелинейному
программированию, так как имеет целевую
функцию, заданную в нелинейном
виде.
Задача дробно-линейного
программирования в общем виде
записывается следующим образом:
Начало формы Целевая функция
Количество
предприятий:
Конец формы
Рассмотрим задачу
дробно-линейного программирования
Будем считать, что d1x1+d2x2 ≠ 0. Математическая модель задачи дробно-линейного программирования может быть использована для определения рентабельности затрат на производство изделий, рентабельности продаж, затрат в расчете на рубль выпускаемой продукции, себестоимости изделий. ПРИМЕР №1. Для производства двух видов изделий A и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Известно время обработки каждого из изделий и затраты, связанные с производством одного изделия.
Оборудование
I и III типов предприятие может использовать
не более 26 ч и 39 ч соответственно,
оборудование II типа целесообразно
использовать не менее 4 ч.
Определить,
сколько изделий каждого вида следует
изготовить предприятию, чтобы средняя
себестоимость одного изделия была
минимальной.
Решение. Составим
математическую модель задачи. Пустьх1 –
количество изделий видаА,которое
следует изготовить предприятию,х2 –количество
изделий видаВ.Общие затраты на их
производство составят (2х1+3х2)
тыс. руб., а средняя себестоимость
одного изделия будет равна
Математическая
модель задачи примет вид
ПРИМЕР №2.
Решить задачу дробно-линейного
программирования симплексным
методом.
В последней оценочной строке есть отрицательные оценки, поэтому нужно делать шаг симплекс-метода. Выбираем столбец с наименьшей оценкой, а затем разрешающий элемент – по наименьшему отношению свободных членов к коэффициентам столбца. Результат шага запишем в таблицу. Аналогично будем повторять шаги.
Получили
решение
ПРИМЕР №3. Рассмотрим следующую задачу. Завод выпускает продукцию n видов p1,…,pn. В процессе производства используются mвидов сырья S1,…,Sm, запасы которого ограничены. Требуется составить производственный план таким образом, чтобы обеспечить максимально возможную рентабельность работы заводов. Нормы расхода сырья, его запасы, а также удельные и условно постоянные затраты и прибыль, получаемая заводом от реализации одного изделия, приведены в таблице 2. Таблица 2 - Исходные данные
Определения:
1.
Рентабельность – показатель,
представляющий собой отношение прибыли
к сумме затрат на производство (%).
2.
Условно-переменные (удельные) затраты
– затраты, которые изменяются прямо
пропорционально объемам выпуска
товаров (затраты на материалы, энергию,
комплектующие, зарплату).
3.
Условно-постоянные затраты – затраты,
которые практически не зависят от
изменения количества выпускаемой
продукции (затраты на освещение,
арендная плата и др.).
Пусть
x1,..,xn– объем выпуска
продукции p1,…,pn Математическая
модель будет иметь вид:
ПРИМЕР
№4.
Решение.
16. Условие выпуклости функций нескольких переменных. 3.4.2.1 Необходимые и достаточные условия выпуклости (вогнутости) функции Для определения выпуклости (вогнутости) функции на некотором интервале можно использовать следующие теоремы.
Теорема 1. Пусть
функция
Теорема 2. Пусть
функция
определена
и непрерывна вместе со своей
производной
на
и
имеет внутри
непрерывную
вторую производную
Докажем теорему 2 для случая выпуклости функции .
Необходимость.
Возьмем произвольную точку
Уравнение касательной к кривой в точке, имеющей абсциссу :
Тогда превышение кривой над касательной к ней в точке равно
Таким образом,
остаток
Значит, график
функции
лежит
выше касательной Достаточность. Пусть кривая выпукла на промежутке . Возьмем произвольную точку . Аналогично предыдущему разложим функцию около точки в ряд Тейлора
Превышение
кривой
над
касательной к ней в точке, имеющей
абсциссу
,
определяемой выражением
Так как превышение
положительно для достаточно малой
окрестности точки
,
то положительна и вторая производная
Пример. Исследовать
на выпуклость (вогнутость) функцию
Ее
производная
Ее вторая
производная 3.4.2.2 Точки перегиба Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута. Из этого определения следует, что точки перегиба — это точки точки экстремума первой производной. Отсюда вытекают следующие утверждения для необходимого и достаточного условий перегиба.
Теорема
(необходимое условие перегиба). Для
того чтобы точка
являлась
точкой перегиба дважды дифференцируемой
функции Теорема (достаточное условие перегиба). Если вторая производная дважды дифференцируемой функции при переходе через некоторую точку меняет знак, то есть точка перегиба.
Отметим, что в
самой точке вторая производная Геометрическая интерпретация точек перегиба иллюстрируется рис. 3.9
В окрестности
точки 3.4.2.3 Исследование функции на выпуклость и наличие точек перегиба 1. Найти вторую производную .
2. Найти точки, в
которых вторая производная
Рис. 3.9. Точки перегиба. 3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости или вогнутости и наличии точек перегиба.
Пример. Исследовать
функцию
1.
2. Вторая производная
равна нулю при
3. Вторая
производная
На интервале
На интервале 3.4.2.4 Общая схема исследования функций и построения графика При исследовании функции и построении ее графика рекомендуется использовать следующую схему:
Исследование функции проводится одновременно с построением ее графика.
Пример. Исследовать
функцию
1. Область
определения функции —
2. Исследуемая
функция — четная
3. Знаменатель
функции обращается в ноль при
Точки
являются
точками разрыва второго рода, так как
пределы слева и справа в этих точках
стремятся к
4. Поведение функции в бесконечности.
поэтому график
функции имеет горизонтальную
асимптоту 5. Экстремумы и интервалы монотонности. Находим первую производную
Находим вторую производную
Так как 6. Интервалы выпуклости и точки перегиба.
Функция
Функция Функция нигде не обращается в ноль, значит точек перегиба нет. 7. Точки пересечения с осями координат.
Уравнение
Уравнение С учетом проведенного исследования можно строить график функции
Схематически
график функции
Рис. 3.10. График функции 3.4.2.5 Асимптоты графика функции
Определение.
Асимптотой графика функции y
= f(x) называется прямая, обладающая
тем свойством, что расстояние от точки
( Асимптоты бывают 3 видов: вертикальные (см. рис. 3.11а), горизонтальные (см. рис. 3.11б) и наклонные (см. рис. 3.11в). Асимптоты находят, используя следующие теоремы:
Теорема 1. Пусть
функция
определена
в некоторой окрестности точки
(исключая,
возможно, саму эту точку) и хотя бы
один из пределов функции при Вертикальные асимптоты следует искать в точках разрыва функции . Теорема 2. Пусть функция определена при достаточно больших и существует конечный предел функции
Тогда прямая
Рис. 3.11. Асимптоты Теорема 3. Пусть функция определена при достаточно больших и существуют конечные пределы
и
Тогда
прямая Пример. Найти асимптоты графика дробно-рациональной функции
Если
Особая точка Перепишем дробно-рациональную функцию в виде:
Так как
Найдём предел
Пример. Найти
асимптоты кривой
Поэтому
Теперь ищем
Функция
имеет
наклонную асимптоту 3.4.2.6 Свойства функций, непрерывных на отрезке. Теоремы Вейерштрасса
(см. рис. 3.12а).
Рис. 3.12. Иллюстрации к теоремам Вейерштрасса 17. Условия Куна-Таккера в задаче нелинейного программирования.
Найти
векторы
Прежде всего проиллюстрируем условия Куна — Таккера на примере. Пример 3
Минимизировать
при ограничениях Решение. Записав данную задачу в виде задачи нелинейного программирования (0)-(2), получим
Уравнение (3), входящее в состав условий Куна—Таккера, принимает следующий вид:
откуда
Неравенства (4) и уравнения (5) задачи Куна — Таккера в данном случае записываются в виде
Уравнения (5.16), известные как условие дополняющей нежесткости, принимают вид
Заметим, что на
переменные Таким образом, этой задачи условия Куна—Танкера записываются в следующем виде:
18. Пример задач нелинейного программирования и графический метод их решения.
В общем виде
задача нелинейного программирования
(ЗНП) формулируется следующим образом:
найти решение X*=
при котором целевая функция
(7) принимает наибольшее (или наименьшее) значение. Предполагается , что хотя бы одна из функций в (6) или в (7) не линейна. Для ЗНП в отличие от ЗЛП нет единого метода решения. В зависимости от вида целевой функции (7) и системы ограничений (6) разработаны специальные методы решения, например, метод множителей Лагранжа для ЗНП с системой ограничений, состоящей только из уравнений, и при условии, что все функции в (6) и (7) имеют непрерывные частные производные. В ЗНП разыскивается наибольшее или наименьшее значение целевой функции – ее глобальный максимум или глобальный минимум. Однако целевая функция может иметь локальные экстремумы, что затрудняет решение ЗНП, так как большинство существующих методов нелинейного программирования не позволяет установить, является ли найденный экстремум локальным или глобальным. ЗНП с двумя переменными может быть решена графически, как было показано в предыдущих разделах. Графическое решение задачи может быть разбито на следующие части:
1. В прямоугольной
системе координат
2. Определяется
тип линий уровня целевой функции 3. Находится линия уровня целевой функции с наибольшим (или наименьшим) значением уровня или устанавливается неразрешимость задачи из-за неограниченности функции на множестве решений системы (6). 4. Определяются координаты точки области решений системы (6), через которую проходит линия уровня, найденная в пункте 3. Пример. Найти неотрицательное решение системы неравенств
(8)
при котором
функция
Решение. Область
неотрицательных решений системы (8)
состоит из двух частей – криволинейных
четырехугольников ABCD и EFGH (рис. 1.3),
ограниченных осями координат,
прямыми
Линиями уровня функции =cявляются окружности с центром в начале координатO(0, 0). Окружность наибольшего радиуса, имеющая общие точки с областью решений системы (8), пройдет либо через точкуD, либо через точкуF, так как эти точки наиболее удалены от начала координат. Найдем координаты точекDиF, решая системы
и получим, что D= (2/3, 6) иF= (7, 4/7).
следовательно,
max 19. Метод множителей Лагранжа нахождения условного экстремума. Метод Лагранжа ─ это метод решения задачи условной оптимизации, при котором ограничения, записываемые как неявные функции, объединяются с целевой функцией в форме нового уравнения, называемоголагранжианом. Рассмотрим частный случай общей задачи нелинейного программирования: Дана система нелинейных уравнений (1): (1) gi(x1,x2,…,xn)=bi(i=1..m), Найти наименьшее (или наибольшее) значение функции (2) (2) f(х1,х2,…,хn), если отсутствуют условия неотрицательности переменных и f(х1,х2,…,хn) иgi(x1,x2,…,xn) ─ функции, непрерывные вместе со своими частными производными. Чтобы найти решение этой задачи, можно применить следующий метод: 1. Вводят набор переменных λ1,λ2,…,λm, называемых множителями Лагранжа, составляют функцию Лагранжа (3)
(3)
F(х1,х2,…,хn,λ1,λ2,…,λm)
=f(х1,х2,…,хn)+ 2. Находят частные производные от функции Лагранжа по переменным xiиλiи приравнивают их нулю. 3. Решая систему уравнений, находят точки, в которых целевая функция задачи может иметь экстремум. 4.Среди точек, подозрительных не экстремум, находят такие, в которыхдостигается экстремум, и вычисляют значения функции в этих точках. 4. Сравнить полученные значения функции fи выбрать наилучшее. Задача: По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве х1 изделия Iспособом затраты равны 4*х1+х1^2 руб., а при изготовлении х2 изделийIIспособом они составляют 8*х2+х2^2 руб. Определить, сколько изделий каждым из способов следует изготовить, так чтобы общие затраты на производство продукции были минимальными. Решение: Математическая постановка задачи состоит в определении наименьшего значения функции двух переменных: f= 4*x1+x1^2 +8*x2 +x2^2, при условииx1 +x2 = 180. Составим функцию Лагранжа: F(x1,x2,λ) = 4*x1+x1^2+8*x2+x2^2+λ*(180-x1-x2). Вычислим ее частные производные по х1,х2, λи приравняем их к 0:
Перенесем в правые части первых двух уравнений λи приравняем их левые части, получим 4 + 2*x1 = 8 + 2*x2, илиx1 −x2 = 2. Решая последнее уравнение совместно с уравнением x1 +x2 = 180, находимx1 = 91,x2 = 89, то есть получили решение, удовлетворяющее условиям: x1,x2 ≥ 0. Найдем значение целевой функции fпри этих значениях переменных: F(x1,x2) = 17278 Эта точка является подозрительной на экстремум. Используя вторые частные производные, можно показать, что в точке (91,89) функция fимеет минимум. Можно сравнить это значение со значением fв соседних точках: f(90,90) = 17280 >17278 =f(91,89). 20. Достаточные условия экстремума ФНП (по второму дифференциалу). Необходимое условие экстремума.
Теорема. Если
дифференцируемая функция
Доказательство: Докажем,
например, равенство нулю частной
производной
Частная производная
функции
по х в
точке
есть
производная функции
Следовательно,
Аналогично можно
показать, что
Эти условия имеют
простой геометрический смысл. Они
означают, что в точках экстремума
касательная плоскость к графику
функции
параллельна
плоскости ХОУ, т. к. в этом
случае уравнение касательной плоскости
имеет вид Замечание. В точках экстремума хотя бы одна из частных производных может не существовать.
Точки, в которых
первые частные производные Из изложенного следует, что точки экстремума функции надо искать в её критических точках. 2. Достаточные условия экстремума. Существуют критические точки, не являющиеся точками экстремума. Ответ на вопрос, имеет ли функция в критической точке экстремум, дают достаточные условия экстремума.
Пусть для
функции
точка
является
критической точкой. Обозначим:
Теорема 5. Если
в критической точке
Если
Если Пример.
1) Определим критические точки
1) В точке
2)
3)
или
Вывод: экстремума нет.
2)
21. Система уравнений фирмы (равенство предельного продукта данного ресурса его цене). 22. Модель прибыли фирмы. Существует значительное количество моделей, позволяющих объяснить поведение коммерческих фирм и их управляющих в терминах их задач и целей. В их число вошли следующие модели: - максимизации прибыли, - максимизации продаж, - максимизации роста, - управленческого поведения - японская модель, направленная на максимизацию добавленной стоимости. Экономисты давно склонны считать, что главной целью организации любого типа должна быть максимизация ее выгод по отношению к затратам. Для коммерческой организации выгоды, которые она стремится получить, выражаются в форме прибыли. Поскольку наша экономическая система позволяет фирмам в нерегулируемых отраслях получать столько, сколько они смогут получить, первоначально предполагалось, что поведение фирмы наилучшим образом может быть описано при помощи модели максимизации прибыли, разработанной исследователями по теории микроэкономики фирмы.
Ранее варианты моделей максимизации прибыли сосредоточивались на решениях, максимизирующих прибыль в краткосрочной перспективе, т.е. позволяющих максимизировать суммарный краткосрочный доход за вычетом общих затрат. В более поздних вариантах таких моделей предполагалось, что цель фирмы состоит в максимизации стоимости фирмы в перспективе на будущее. Поскольку стоимость фирмы в длительном интервале определяется потоком ее будущих прибылей, которые могут соответствовать, а могут и не соответствовать ожиданиям, модель должна быть развита с тем, чтобы включить в нее текущую стоимость будущих денег (будущих прибылей) и концепцию риска. Для понимания такой модели студент должен четко представлять себе концепцию текущей стоимости.
Текущая стоимость – сегодняшняя стоимость суммы, которая будет получена в будущем, дисконтированная на основе той или иной процентной ставки
Концепция текущей стоимости основана на принципе сложных процентов. Предположим, что сегодня инвестирован 1 долл. при годовой процентной ставке i. Тогда через год сумма A1 равная основному капиталу и процентам, составит
Процесс, обратный процессу начисления сложных процентов, называется дисконтированием. Если мы ожидаем, что А2 через два года будет равно $1(1 + i)2, то дисконтированная текущая стоимость 1 долл. при процентной ставке i составит
В общем виде концепция текущей стоимости (PV) будущих прибылей, p, выражается как
где PV отражает текущую стоимость будущих прибылей, p, получаемую к концу периода дисконтирования в n лет при свободной от риска периодической ставке дисконта i, выражаемой десятичной дробью. Иначе говоря, если будущие прибыли считаются достоверными, то может быть использована ставка дисконта без учета риска, равная i. Если будущий доход нельзя считать гарантированным, то мы используем рисковую ставку дисконтирования r, определяемую как i плюспремия за риск, компенсирующая его. Таким образом, величина r отражает степень риска. Это будет норма капитализации или стоимости капитала фирмы, т.е. та норма дохода, которую потребуют инвесторы после изучения экономического положения фирмы и финансового риска.
Независимо от того, какую переменную вы используете (i или r), модель позволит максимизировать текущую стоимость дисконтированного потока прибылей. Если ожидается, что поток прибылей будет изменяться по годам, то уравнение можно привести к следующему виду:
де p1 p 2, p 3 и pn представляют прибыли, ожидаемые фирмой в первом, втором, третьем и n-м годах при рисковой ставке дисконта г или требуемой норме дохода.
Если ожидается в каждом году получать равную прибыль, то задача максимизации потока прибылей существенно упрощается и сводится к задаче максимизации к. Текущая стоимость потока равных прибылей может быть вычислена по формуле (5), однако будет значительно проще воспользоваться формулой
где p— периодические платежи; r — рисковая ставка дисконта; n - количество периодов.
Выражение в скобках называется показателем дисконтирования. Его вывод приведен в Приложении 2А в конце данной главы, а показатель дисконтирования при переменной величине годовой дисконтной ставки представлен в табл. А Приложения, помещенного в конце данной книги.
В динамической ситуации, когда предполагается возможность изменения величины p, задача максимизации значительно усложняется и приходится использовать уравнение (5). Однако для практического ее решения часто бывает полезно предположить равномерное распределение годовой прибыли на перспективу и считать, что эта тенденция сохранится до тех пор, пока изменение условий (ввод в эксплуатацию нового завода) не потребует изменить исходное предположение.
Если ожидаемый поток равномерной годовой прибыли, U, сохраняется постоянным в неограниченном интервале времени (т.е. бесконечно), то текущая стоимость такой последовательности доходов, PV, примет вид
где r — норма капитализации, характеризующая бизнес данной фирмы и ее финансовый риск.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






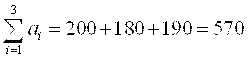 ,
, 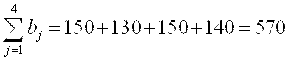 .
.
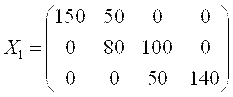


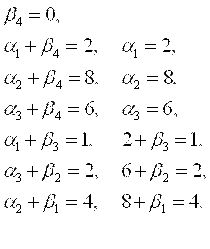











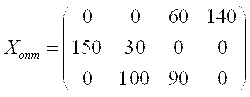
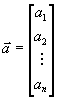 ,
, 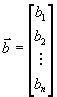 ,
,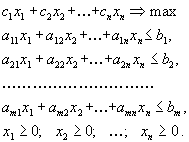
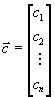 ;
; 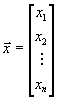 ;
,
;
,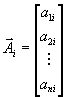 ,
, 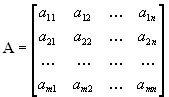 .
.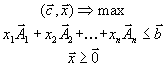
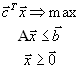
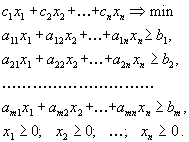
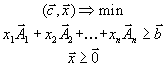
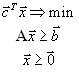
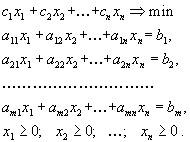
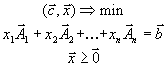
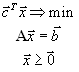
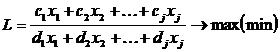 при
ограничениях
при
ограничениях
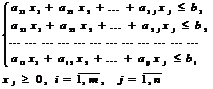 ,
где сj,dj,bi,aij –
постоянные коэффициенты.
d1x1+d2x2+...+dnxn ≠
0
,
где сj,dj,bi,aij –
постоянные коэффициенты.
d1x1+d2x2+...+dnxn ≠
0



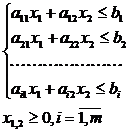
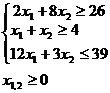 .
Задачу
дробно-линейного программирования
можно свести к задаче линейного
программирования и решить симплексным
методом.
Обозначим
.
Задачу
дробно-линейного программирования
можно свести к задаче линейного
программирования и решить симплексным
методом.
Обозначим
 при
условии
при
условии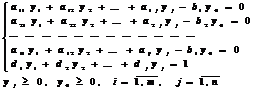 После
нахождения оптимального решения
полученной задачи, используя
вышеуказанные соотношения, находят
оптимальное решение исходной задачи
дробно-линейного программирования.
После
нахождения оптимального решения
полученной задачи, используя
вышеуказанные соотношения, находят
оптимальное решение исходной задачи
дробно-линейного программирования.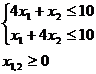 .
Решение. Сведем
данную задачу к задаче линейного
программирования. Сначала введем
дополнительные переменные, чтобы
привести задачу к каноническому
виду:
при
ограничениях
.
Решение. Сведем
данную задачу к задаче линейного
программирования. Сначала введем
дополнительные переменные, чтобы
привести задачу к каноническому
виду:
при
ограничениях
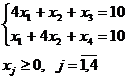 .
Обозначим
.
Обозначим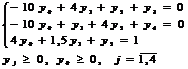 .
Решим
полученную задачу симплекс-методом.
Введем дополнительную переменную,
чтобы получить единичный базис:
.
Решим
полученную задачу симплекс-методом.
Введем дополнительную переменную,
чтобы получить единичный базис:
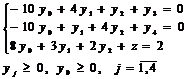 .
Составляем
симплекс-таблицу.
.
Составляем
симплекс-таблицу.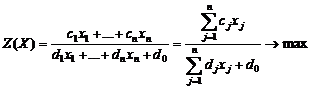
 Рис.
1- Геометрическая интерпретация
задачи
Ограничения задачи –
это множество допустимых решений,
лежащих в четырехугольникеАВСО.
Целевая функция задачи – линии уровня
цели, проходящие через точку S.
Координаты точки S определяются в
результате решения системы
уравнений:
(числитель целевой
функции);
Рис.
1- Геометрическая интерпретация
задачи
Ограничения задачи –
это множество допустимых решений,
лежащих в четырехугольникеАВСО.
Целевая функция задачи – линии уровня
цели, проходящие через точку S.
Координаты точки S определяются в
результате решения системы
уравнений:
(числитель целевой
функции);


 и
построить ее график.
и
построить ее график.








 .
.


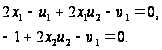
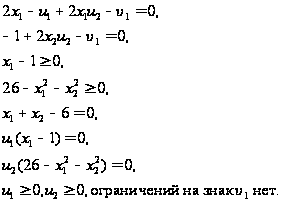
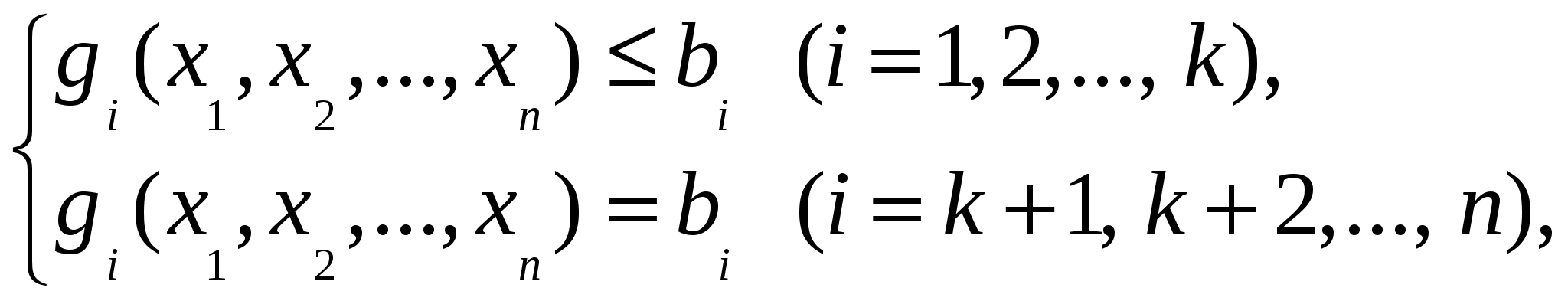
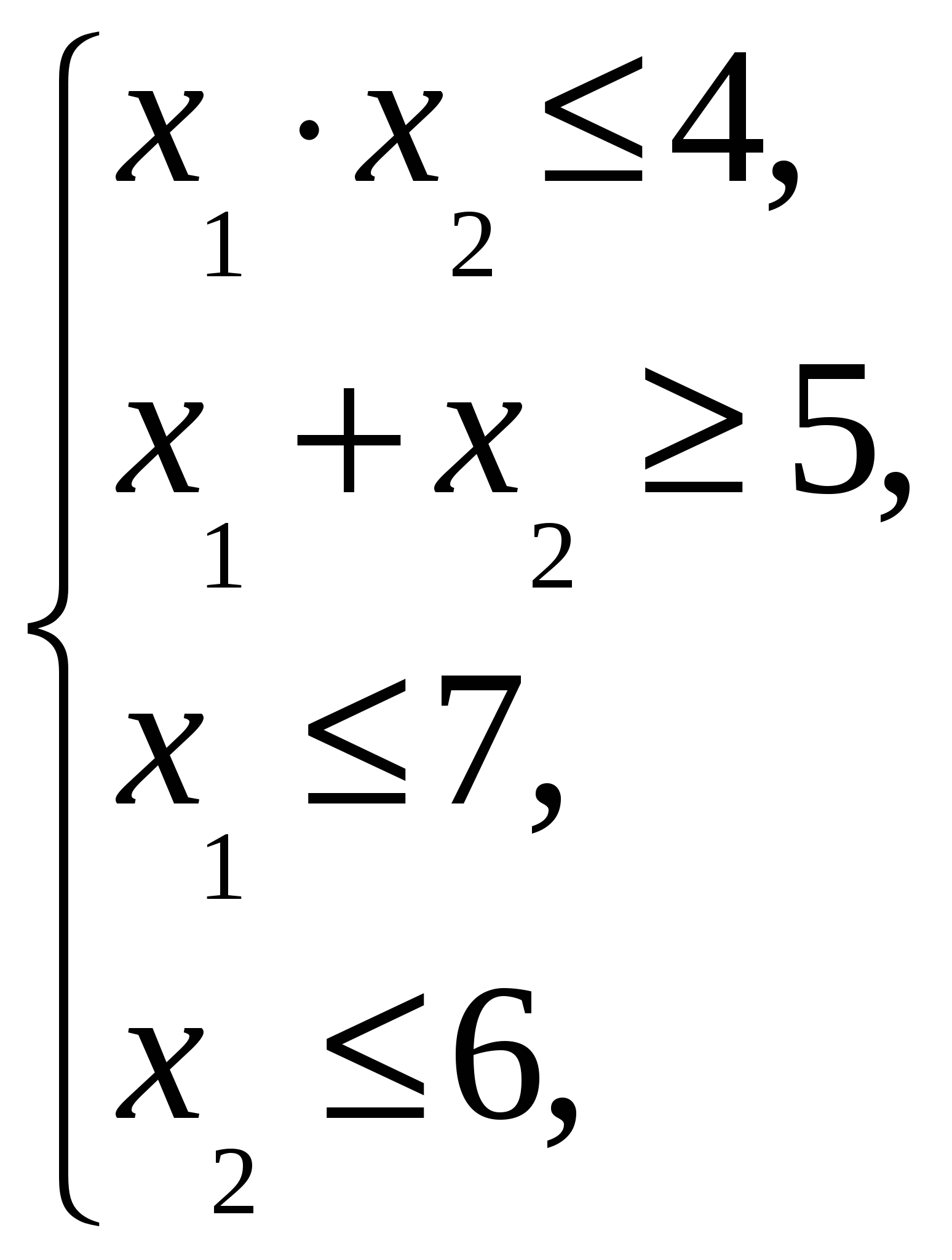

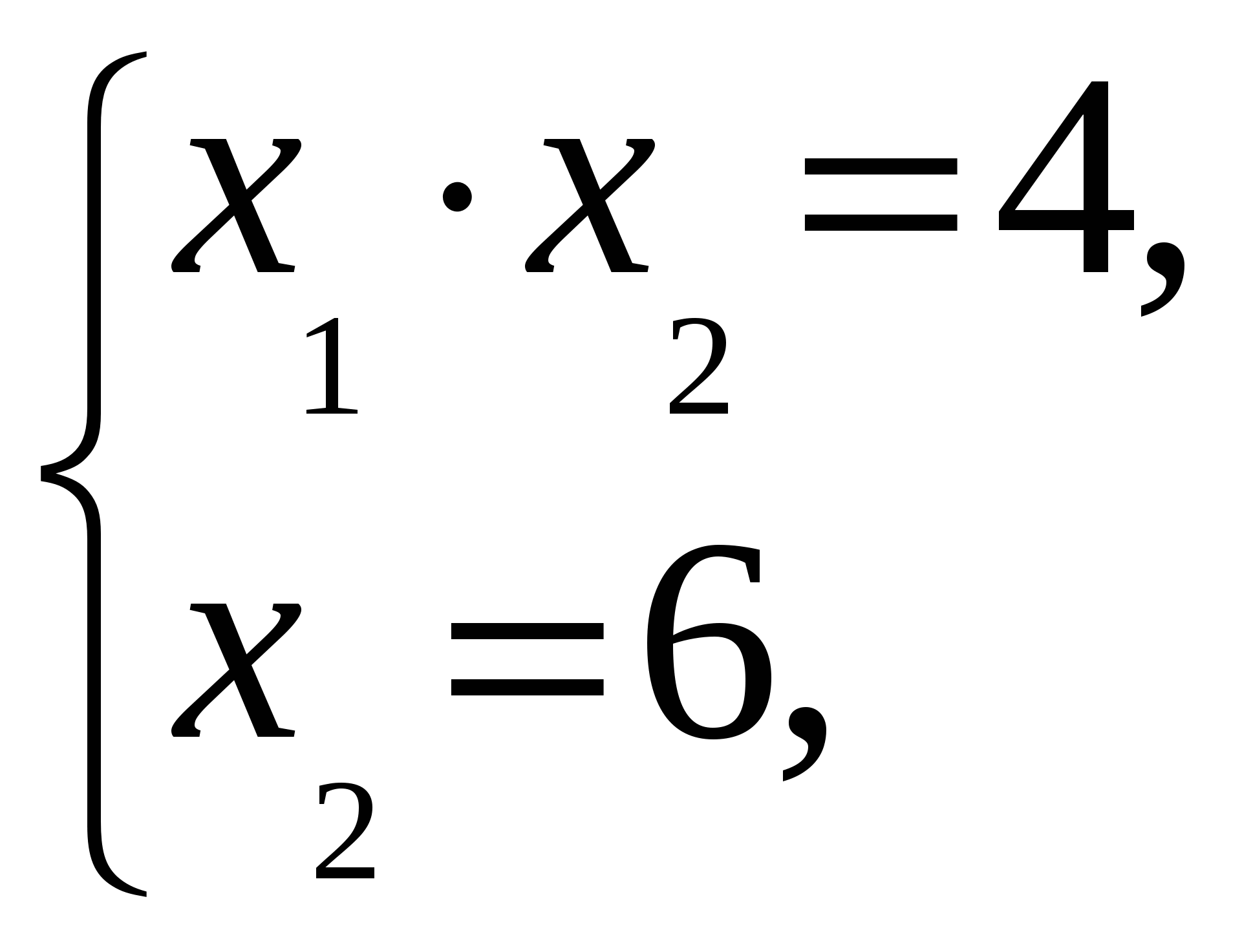
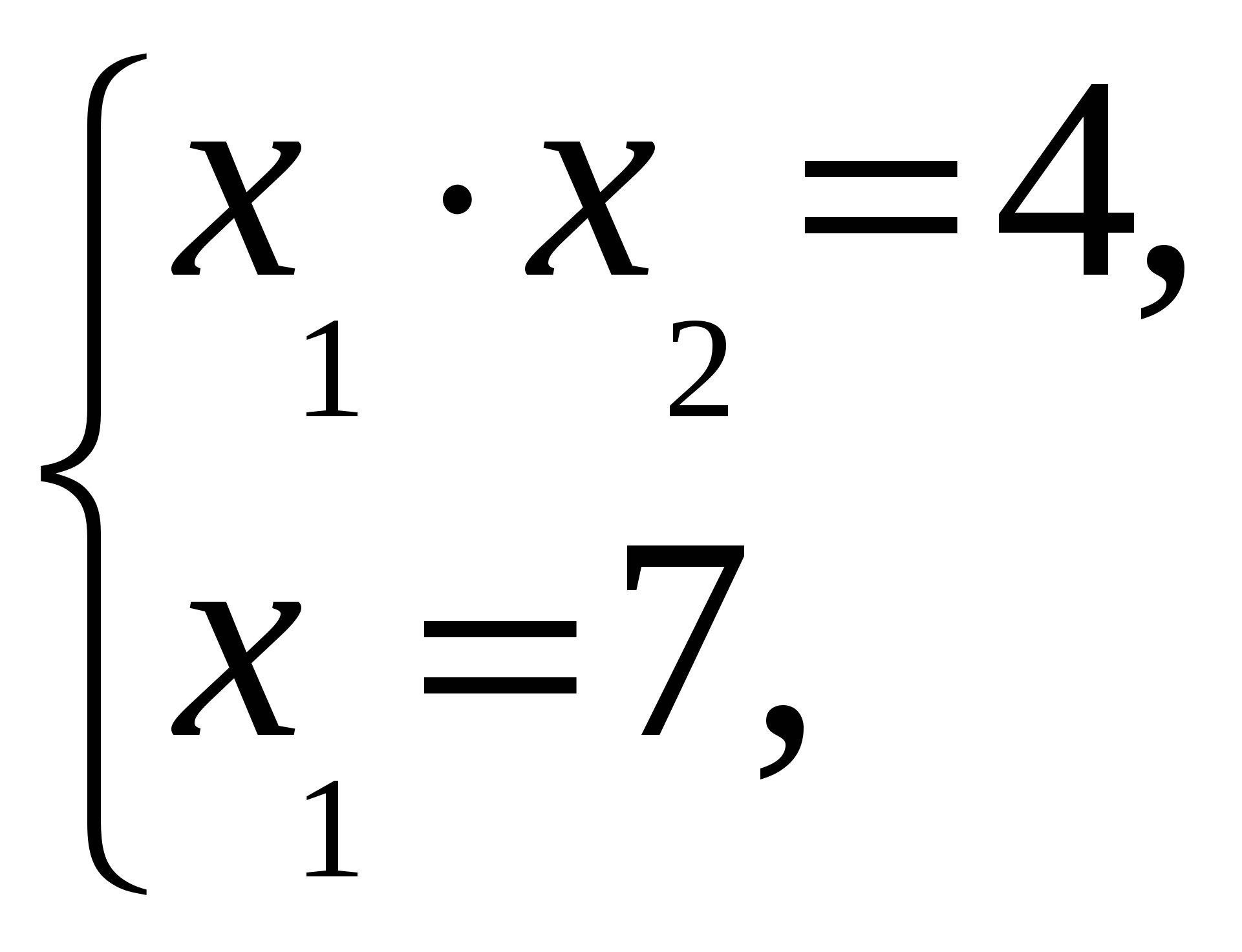
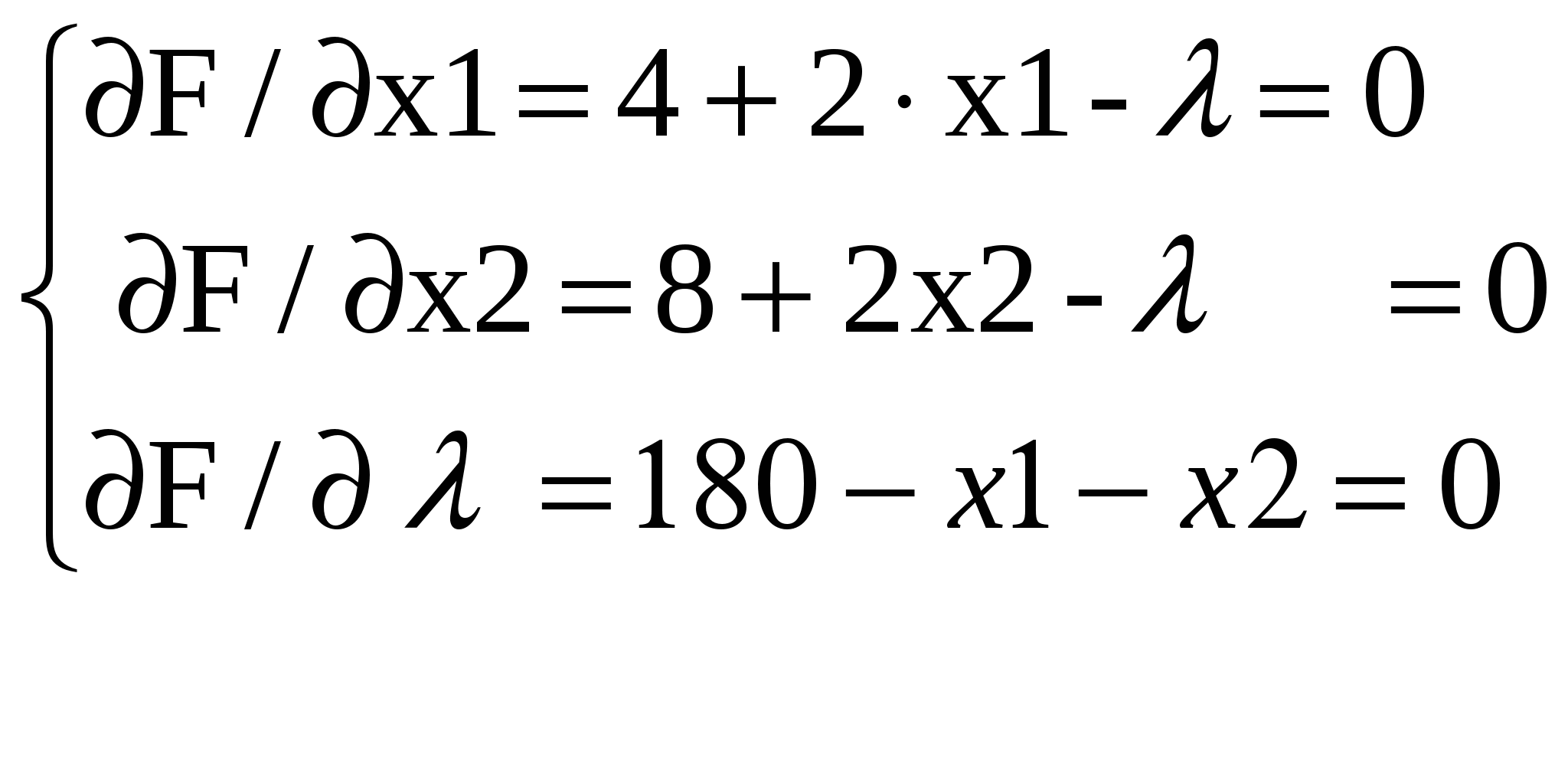
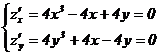
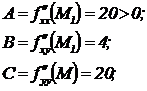
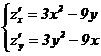
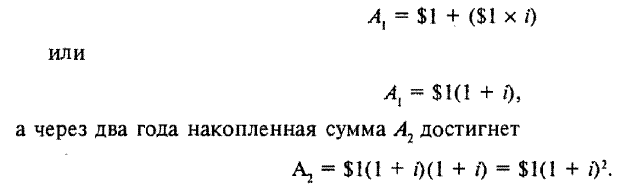
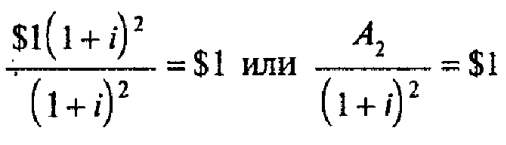
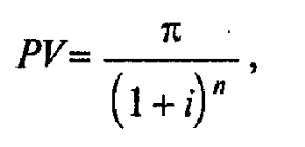
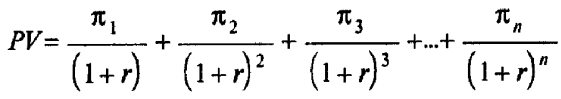 (5)
(5)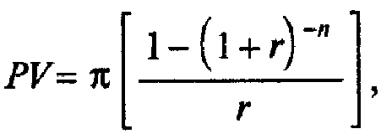 (6)
(6)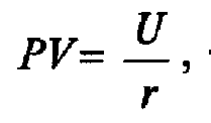 (7)
(7)