1.Напишите определение автокорреляционной функции сигнала s(t ).

Автокорреляционная функция — зависимость взаимосвязи между функцией (сигналом) и ее сдвинутой копией от величины временного сдвига.

Для детерминированных сигналов автокорреляционная функция (АКФ) сигнала {\displaystyle f(t)} определяется интегралом:

{\displaystyle \Psi (\tau )=\int _{-\infty }^{\infty }f(t)f^{*}(t-\tau )\mathrm {d} t}

и показывает связь сигнала (функции  {\displaystyle \;f(t)}) с копией самого себя, смещённого на величину {\displaystyle \tau } . Звездочка означает комплексное сопряжение

Свойства автокорреляционной функции.

1. Если , то Автокорреляционная функция при расстройке τ =0 принимает свое максимальное и положительное значение, равное энергии самого сигнала.

2 .Автокорреляционная функция является четной функцией.

Данное выражение легко доказать, сделав следующую замену вида .

Тогда. (2)

3.При любом модуль автокорреляционной функции не превосходит энергии сигнала.

.

Данное выражение вытекает из неравенства Коши.

.

Это свойство еще раз показывает, что с увеличением времени АКФ сигнала должна уменьшаться. Ее максимум находится в точке и равен энергии сигнала.

4.Данное свойство вытекает из предыдущих. Если проанализировать АКФ относительно энергии сигнала , то максимальное значение АКФ равно ±1, а при τ > t_и характеристика B_U (τ) будет принимать нулевое значение.

Пределы изменения АКФ от –1, до1 и с возрастанием она затухает.

Геометрический смысл автокорреляционной функции заключается в определении площади пересечения функции   и её копии, сдвинутой на время x (Рис.2)

 

Рис. 2

Изменяя время сдвига x до тех пор, пока сигнал и его копия перестанут пересекаться (в данном случае  ), получим АКФ  . Очевидно, что при изменении знака сдвига при одинаковой его величине функция автокорреляции одинакова, т.е.  , что говорит о четном её характере. Ясно, что при x=0автокорреляционная функция имеет максимум, при этом

а в свою очередь полная энергия сигнала равна

Таким образом, максимум автокорреляционной функции определяет полную энергию сигнала. При увеличении сдвига x АКФ убывает до нуля.

1.1. Автокорреляционные и взаимно-корреляционные функции фазоманипулированных сигналов

Будем рассматривать сложные (псевдошумовые, псевдослучайные, с расширенным спектром) амплитудно-фазо-манипулированные сигналы (АФМ-сигналы), являющиеся последовательностями элементарных радиоимпульсов с прямоугольной огибающей, длительностью , одинаковой частотой несущего колебания и разными амплитудами и начальными фазами:

101\* MERGEFORMAT (.)

Здесь - номер сложного сигнала, длительность этого сигнала, - число элементарных символов сложного сигнала (база сигнала), и - амплитуда и начальная фаза -го элементарного символа -го сигнала. Функция

определяет форму огибающей элементарного символа.

Часто вместо 01 используют другую запись для сложного сигнала:

,

где

202\* MERGEFORMAT (.)

- комплексная огибающая радиосигнала .

Для другого сложного АФМ-сигнала с номером комплексную огибающую также можно записать в форме, аналогичной 02:

, . 303\* MERGEFORMAT (.)

Наиболее простыми для практического использования являются сигналы, для которых , , т.е. амплитуды элементарных символов одинаковы, а фазы принимают лишь два возможных значения 0 и . В этом случае комплексные амплитуды элементарных символов оказывается вещественными, поскольку и . Здесь . Такие сигналы называют сложными фазоманипулированными (ФМ-сигналами).

Комплексная огибающая (1.3) ФМ-сигнала является вещественной

, ,

и полностью определяется кодовой последовательностью

. 404\* MERGEFORMAT (.)

Автокорреляционная функция (АКФ) радиосигнала , , определяется равенством [1]:

, ,. 505\* MERGEFORMAT (.)

где - энергия сигнала.

Аналогичным образом определяется взаимная корреляционная функция двух сложных сигналов и :

, . 606\* MERGEFORMAT (.)

Известно также, что функции 05 и 06 могут быть вычислены по комплексным огибающим этих сигналов:

, 707\* MERGEFORMAT (.)

где

, , 808\* MERGEFORMAT (.)

есть комплексная огибающая ВКФ. Здесь , .

В частности для исследуемых в данной работе ФМ-сигналов

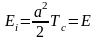, . 909\* MERGEFORMAT (.)

Для любых допустимых значений и интеграл в 09 для прямоугольной огибающей элементарных сигналов можно вычислить по формуле:

где

треугольная функция, отличная от нуля только на интервале и имеющая максимальное значение 1 при . В результате комплексная огибающая ВКФ 09 двух ФМ-сигналов с расширенным спектром принимает вид:

10010\* MERGEFORMAT (.)

и является вещественной функцией.

Введя обозначение , меняя порядок суммирования и учитывая 09, окончательно получаем:

. 11011\* MERGEFORMAT (.)

В соответствии с 011 комплексная огибающая ВКФ двух ФМ-сигналов и вида 01 является суммой вещественных треугольных функций, сдвинутых друг относительно друга на время, кратное , и имеющих коэффициенты

12012\* MERGEFORMAT (.)

которые могут принимать положительные и отрицательные значения.

На основании 07 и 010 для взаимной корреляционной функции двух радиосигналов и можно записать:

. 13013\* MERGEFORMAT (.)

В частном случае при из 011, 012 и 013 получаем автокорреляционную функцию радиосигнала.

В формуле 011 каждое слагаемое имеет форму треугольного импульса. Слагаемое с номером называется основным (главным) пиком. Он имеет максимальное значение, равное 1. Импульсы АКФ с номерами , называются боковыми пиками.

2.Напишите определение взаимокорреляционной функции сигналов s (n ) и x (n)

Взаимная корреляционная функция определяет временную связь двух сигналов во времени. Если сигналы не зависимы друг от друга, их корреляционная функция равна нулю. Чем шире корреляционная функция, тем большая степень связи двух сигналов друг с другом.

Взаимная корреляционная функция определяется соотношением

Пример получения взаимной корреляционной функции показан на рис.1. Значение корреляционной функции в любой момент x определяется площадью пересечения функций   и сдвинутой копии  .

Рис. 1

Взаимная корреляционная функция не обязательно симметрична и её максимум может оказаться не в точке x=0.

3.Приведите выражение для начального момента порядка n случайной величины X с характеристической функцией (v ) .

4.Какое устройство осуществляет отображение информационной последовательности { }n a во множество элементарных сигналов { ( )} m s t ? Каково должно быть число элементарных сигналов M для передачи k бит одним элементарным сигналом?

Демультиплексор

M=2^k или k=log2(M)

5. Выразите кумулянты случайной величины X c 1, 2 c , 3 c через её моменты m1 , m2 , m3 .

6.Рассчитайте спектральную эффективность сигнала с модуляцией КАМ-16, шириной основного лепестка спектра 100 кГц и символьной скоростью 64000 символов в секунду.

64000/100000=0.64 бит/с/Гц

Спектральная эффективность системы мобильной связи представляет собой показатель, вычисляемый как отношение скорости передачи данных на 1 Гц используемой полосы частот (бит/с/Гц). Эта величина также характеризует скорость передачи информации в заданной полосе частот. Спектральная эффективность является показателем эффективности использования частотного ресурса и в некоторых случаях — показателем качества услуг.

7.Нарисуйте фазовое созвездие сигнала ФМн-8 (PSK-8). Напишите около каждой точки фазового созвездия значения информационных битов, передаваемые соответствующим элементарным сигналом (отображение битов в элементарные сигналы осуществите по Грею)

8. Пусть сигнал S(t) со скоростью передачи информационных символов R и модуляцией PSK-8 подвергается расширению типа DSSS с использованием ПСП X(t) длиной L. Чему будет равна чиповая скорость сигнала S(t), расширенного последовательностью X(t)? Чему будет равна скорость передачи информации?

9. Рассчитайте спектральную эффективность сигнала с модуляцией КАМ-16, шириной основного лепестка спектра 50 кГц и символьной скоростью 32000 символов в секунду

32000/50000=0,64 (Бит/с:Гц)

10. Сигналы с расширением спектра, кодовые псевдослучайные последовательности (ПСП) и шумоподобные сигналы. Формирование широкополосных двоичных ФМн- сигналов методом DSSS. База сигнала.

Важным свойством метода прямого расширения спектра (direct sequence spread spectrum, DSSS) можно считать то, что ширина спектра сигнала, модулирующего опорную частоту, определяется главным образом параметрами модулирующей последовательности. Для расширения спектра используются так называемые псевдослучайные последовательности (ПСП). Элементарный импульс ПСП называют чипом. Каждый информационный символ после перемножения с ПСП будет отображаться многими чипами.

Сигналы с расширенным спектром являются псевдослучайными, т.е. имеют свойства, аналогичные свойствам случайного процесса или шума, поэтому чаще называются шумоподобными сигналами (ШПС), хотя формируются по вполне детерминированным алгоритмам. ПСП чаще всего является бинарной с элементами 0 и 1 и обладает свойствами, схожими со свойствами случайной бинарной последовательности.

Прямое расширение спектра осуществляется путем перемножения информационного сигнала U_инф(t) на сигнал ПСП r(t). В результате модулирующий сигнал можно записать:

На рисунке 1 показан примерный вид участка исходной битовой последовательности (выделена синим цветом), сигнала ПСП (выделен красным цветом) и их соответствующие спектры:

Рисунок 1 – Вид информационного сигнала, модулированного ПСП (а) и спектральное представление этих сигналов (б)

Важной характеристикой широкополосного сигнала является его база, смысл которой заключается в относительном увеличении полосы частот передаваемого сигнала в радиоканале по сравнению с полосой частот информационного (исходного) сигнала. Величина базы сигнала:

На практике удобнее определять базу сигнала как произведение ширины спектра исходного сигнала на длительность элементарного символа ПСП (чипа) или как отношение длительности символа информационного сигнала к длительности чипа ПСП:

Основными требованиями, предъявляемыми к ПСП, являются:

– ярко выраженный максимум АКФ при нулевом сдвиге между кодовой последовательностью и ее копией;

– низкий уровень боковых пиков АКФ (т.е. при ненулевом сдвиге между кодовой последовательностью и ее копией);

– низкий уровень значений ВКФ при любых относительных сдвигах кодовых последовательностей.

В настоящее время среди бинарных кодовых последовательностей большой длины наибольшее распространение получили М-последовательности, последовательности Лежандра, кодовые последовательности Голда и Кассами, кодовые последовательности Уолша, нелинейные кодовые последовательностей.

Преимущества М-последовательностей большой длины заключается в уменьшении уровня периодических боковых лепестков функции неопределенности М- последовательностей с ростом ее длины L. Максимальный уровень периодического бокового лепестка ВКФ М-последовательности обратно пропорционален длине последовательности (1/L).