Вопросы к Задаче 1

1 Какой стержень называют стержнем большой жесткости?

Стержень большей жесткости – стержень, деформации которого бесконечно малы по сравнению с его размерами.

2 Какова структура формулы для определения нормальных напряжений в произвольной точке поперечного сечения при внецентренно приложенной продольной силе? Какой вид имеет эпюра напряжений?

Внецентренное растяжение (сжатие) представляет собой случай нагружения, при котором линия действия равнодействующей внешних сил параллельна оси стержня z, но не совпадает с ней. Пусть в торцевом сечении стержня в точке А с координатами (х_F, у_F) приложена равнодействующая внешних сил F.

В произвольном поперечном сечении стержня возникают три внутренних силовых фактора, постоянных по его длине:

Здесь х_F  у_F – координаты точки приложения равнодействующей внешней нагрузки F (координаты полюса силы). Таким образом, внецентренное растяжение (сжатие) представляет собой сочетание косого изгиба с центральным растяжением или сжатием. Нормальное напряжение в произвольной точке поперечного сечения В(х, у) определяется следующим выражением:

или

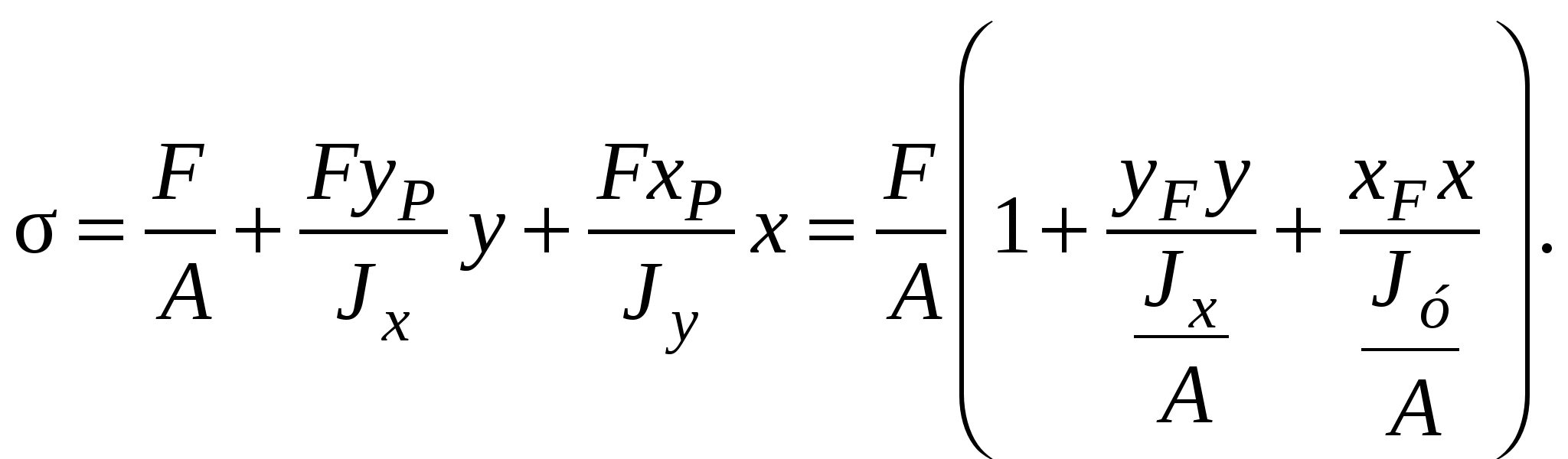
Отношения и представляют собой квадрат радиусов инерции сечения:

.

С учетом этих обозначений формула принимает вид

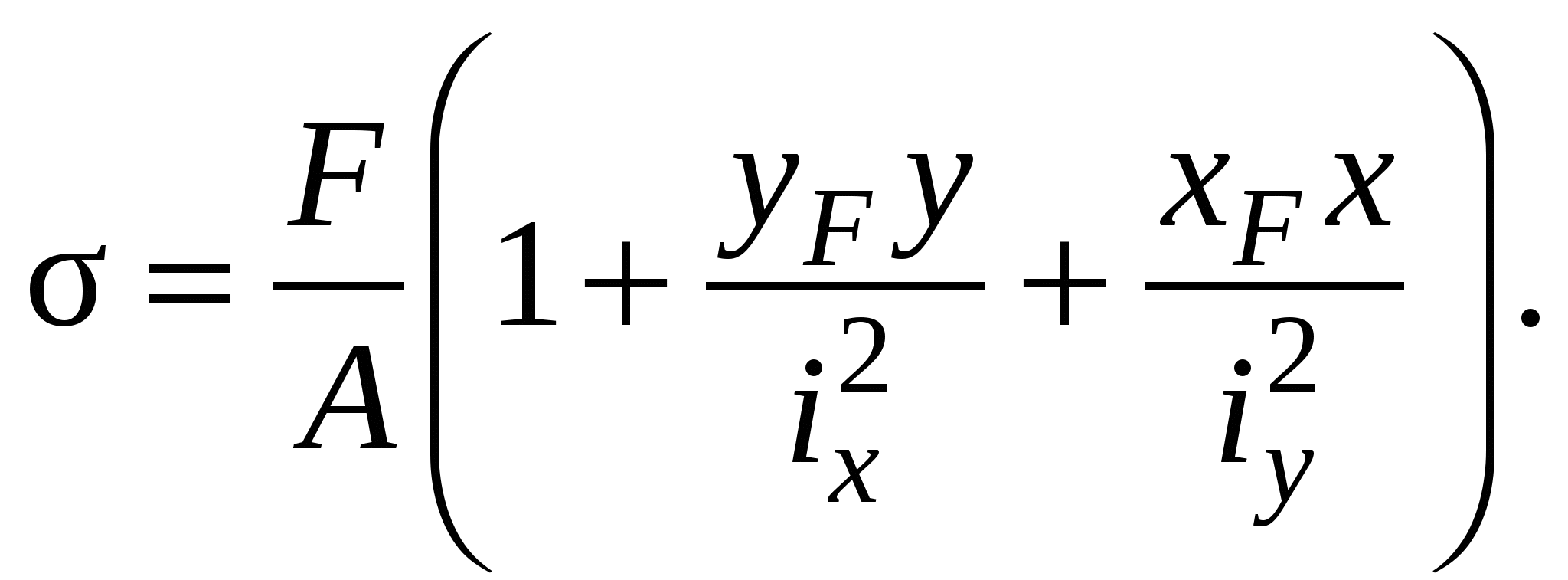
При определении напряжений по формуле величины хF, х, уF, у берутся с учетом их знака относительно координатных осей. В условиях внецентренного сжатия перед правой частью формулы ставится знак минус.

Эпюры напряжений:

3 Как определяется положение нейтральной линии при внецентрированном растяжении или сжатии?

При сложном профиле сечения стержня для определения опасной точки предварительно находится положение нейтральной линии. Учитывая, что на нейтральной линии напряжения равны нулю, тогда:

где х₀ и у₀ – координаты любой точки нейтральной линии. Уравнение нейтральной линии будет иметь вид:

Это – уравнение прямой, не проходящей через начало координат.

По уравнению можно определить отрезки, отсекаемые нейтральной линией на координатных осях. Обозначим эти отрезки через а_хи а_у.

Если принять, что у₀ = 0, х₀ = а_х, то из уравнения получим:

Принимая х₀ = 0, у₀ = а_у, будем иметь:

Решая эти уравнения, получим отрезки, отсекаемые нейтральной линией на координатных осях:

,  .

Исследование этих формул показывает, что точка приложения силы и нейтральная ось лежат по разные стороны относительно центра тяжести сечения.

Нейтральная линия делит поперечное сечение стержня на две зоны – сжатую и растянутую. Проводя параллельно нейтральной линии касательные к контуру сечения, найдем опасные точки С и D, лежащие в растянутой и сжатой зонах.

Условие прочности для стержня из пластичного материала запишется в виде

Где х_оп и y_оп – координаты точки, наиболее удаленной от нейтральной линии.

Для стержней, выполненных из неравнопрочного материала, расчет на прочность ведется для двух опасных точек (в растянутой и сжатой зонах).

Условия прочности имеют вид:

,

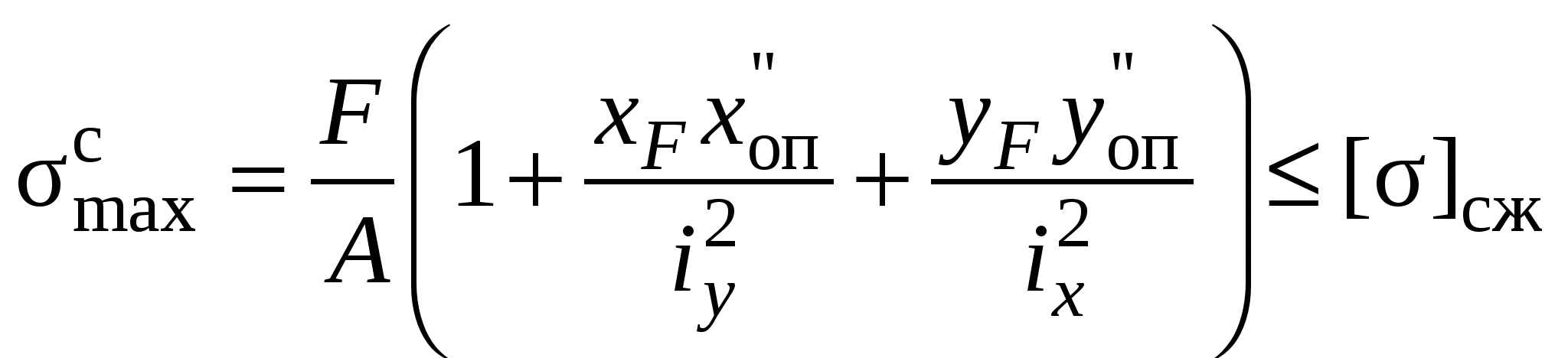
где и – координаты опасных точек соответственно в растянутой и сжатой зонах.

4 Может ли нейтральная линия находиться вне поперечного сечения?

Нулевая линия при косом изгибе не проходит перпендикулярно к силовой линии. Угол между нейтральной и силовой линиями будет прямым, только если главные центральные моменты инерции равны ( ), но это не прямой изгиб.

Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг).

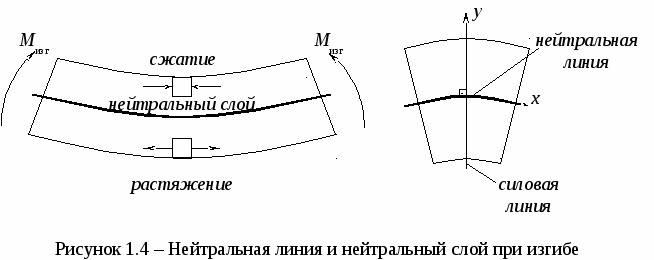
5 В каком случае нейтральная линия перпендикулярна одной из главных осей инерции сечения?

Для нахождения главных осей симметричного сечения достаточно найти положение его центра тяжести. Одной из главных центральных осей является ось симметрии, вторая ось ей перпендикулярна. Если ось, перпендикулярная оси симметрии, проходит и не через центр тяжести сечения, т. е. ось симметрии и любая, ей перпендикулярная, образуют систему главных осей.

Следовательно нейтральная линия перпендикулярна одной из главных осей инерции сечения.