3.4 Работа расширения газа

Взаимодействие тела с соприкасающимися с ним внешними телами можно характеризовать давлением. При взаимодействии может происходить перемещение точек поверхности тела, т.е. изменяться его объем.

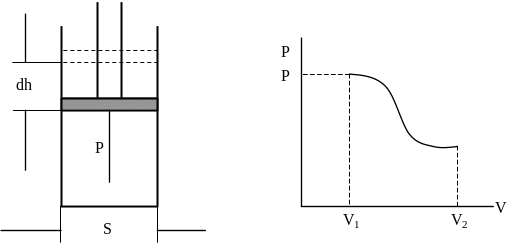
Рис.24.

Подсчитаем элементарную работу dA, совершаемую газом при его расширении:

dA = Fdh = рSdh = pdV.

Полная работа: 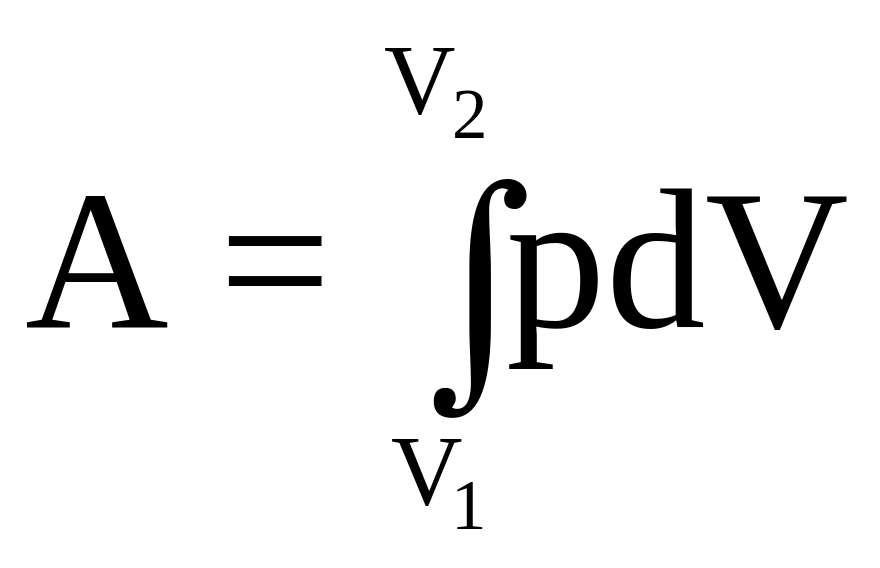. (35)

Если тело расширяется, то V₂>V₁ и А > 0 – работа расширения положительная. Газ совершает работу против внешних сил.

Если тело сжимается, то V₂<V₁ и А < 0 – работа сжатия отрицательная. Внешняя сила совершает работу над телом.

Работа при различных процессах:

а) изотермический:

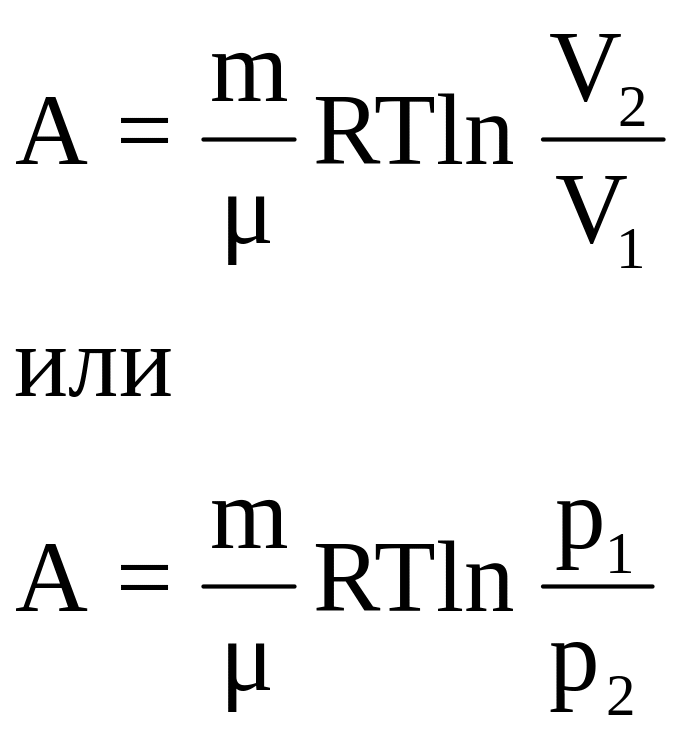, (36)

б) изохорический:

A = 0,

в) изобарический:

A = p (V₂ – V₁). (37)

Опыт№3.1

«Пушка» на моторе. Изохорический нагрев газа.

Цель работы: с помощью данной установки рассмотреть изохорический нагрев газа.

Оборудование:

1. Двигатель, вращающий латунную трубку.

2. Латунная трубка, внутри которой капли этилового спирта.

3. Зажим.

4. Пробка, которой плотно закрыта латунная трубка.

Ход работы

1. Включим двигатель, тем самым приведем латунную трубку во вращение.

2. Зажимом будем тормозить трубку, от трения будет повышаться температура спирта в трубке.

Рис.25. Демонстрация опыта

3. Температура трубки и этилового спирта повышается, давление молекул спирта на пробку увеличивается. Пробка выстреливает.

Рис.26. Демонстрация опыта

Вывод: этиловый спирт получил энергию от латунной трубки, которая нагрелась из-за трения, эта энергия была использована в совершении работы спиртом при выталкивании пробки. При изохорическом нагревании газа давление в газе возросло, что и заставило вылететь пробку из трубки.

Опыт№3.2 Работа расширения газа.

Цель работы: рассмотреть ситуацию, которая наглядно показывает случай, в котором нагретый газ совершает работу.

Оборудование:

1. Пробирка.

2. Вода.

3. Пробка.

4. Свеча.

5. Зажим.

Рис.27. Демонстрация опыта

Ход работы

1. Наполнить пробирку водой и плотно закрыть пробкой.

2. Начать нагревать пробирку с помощью зажженной свечи.

3. Постепенно в пробирке будет образовываться пар.

4. В момент, когда давление пара возрастет до определенного значения, пробка вылетит из пробирки.

Рис.28. Демонстрация опыта

Вывод: при нагревании пар получил энергию от сожженного топлива, расширяясь, он совершил работу – вытолкнул пробку.

3.5 Теплоемкость. Измерение теплоемкостей. Классическая теория теплоемкости и отступление от неё. Закон Дюлонга и Пти

В термодинамике для характеристики тепловых свойств тел используется понятие теплоёмкости.

Если при поглощении количества тепла dQ температура тела повышается на dT, то

dQ ~ dT,

dQ = C_TdT,

– называется теплоёмкостью тела,

.

С_т – не универсальная постоянная для тела, а является функцией условий, при которых происходит нагревание и зависит от свойств тела:

– молярная теплоемкость (теплоемкость моля или киломоля),

,

– удельная теплоемкость (теплоемкость единицы массы),

,

C_т = υC_μ = mC_уд, где – число молей (38)

В зависимости от условий протекания процесса вводят теплоемкости:

С_тР – теплоемкость при р = const:

а) С_Рμ – молярная при p = const;

б) C_уд.р – удельная при p = const;

C_тV – теплоемкость при V = const:

а) C_Vμ – молярная при V = const;

б) C_уд.V – удельная при V = const.

Измерение теплоемкостей твердых и жидких тел обычно производят с помощью калориметра, используя уравнение теплового баланса.

Если нагревание происходит при V = const, то всё тепло переходит во внутреннюю энергию U, тогда согласно определению теплоемкости:

, поэтому

– постоянная величина, независящая от параметров состояния. (39)

Аналогично, если нагревание происходит при постоянном давлении (p = const), то:

– постоянная величина, независящая от параметров состояния. (40)

Объединяя (39) и (40), получим:

C_pμ = C_vμ + R – уравнение Роберта-Майера, (41)

– показатель адиабаты.

Итак:

для изохорического процесса: ,

для изобарического процесса: .