2. Традиционная технология динамического анализа автомобиля

Сложность динамического анализа заключается в невозможности точного аналитического исследования даже несложных механических систем, поскольку динамика описывается системами дифференциальных или дифференциально-алгебраических уравнений, в общем случае нелинейных, решение которых аналитически получить невозможно. Это обуславливает применение численных методов решения данных уравнений

Примерно до середины 70-х годов 20 века технология динамического анализа автомобиля на этапе проектирования заключалась в следующем: после схематизации реальной механической системы вручную составляли систему дифференциально-алгебраических уравнений движения тел модели, затем создавали программу на одном из языков программирования для цифровой ЭВМ для численного решения данной системы уравнений и вывода результатов или собирали электрическую схему на аналоговой ЭВМ, а затем проводили решение данной системы или аналоговое моделирование и выводили результаты в виде графиков изменения динамических показателей системы от времени. На рисунке 6 приведена структурная схема данной технологии.

Постоянный рост требований к качеству проектируемых автомобилей приводит к необходимости построения усложненных динамических моделей. С одной стороны, это вызывает увеличение числа тел модели и учитываемых степеней свободы. С другой стороны, уточняются и усложняются математические модели взаимодействия тел, входящих в систему. Примерами могут служить силы взаимодействия автомобильного колеса с дорогой.

Рис. 6. Схема традиционной технологии моделирования механической системы автоматизированного анализа динамики

На рис. 7. показаны примеры моделей взаимодействия шины с дорогой, используемых в настоящее время для решения задач динамики автомобиля.

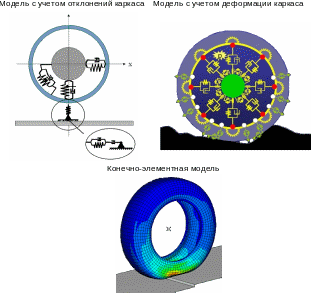
Рис. 7. Примеры моделей шин, используемых в задачах динамики автомобиля

Наконец, наблюдается тенденция к сокращению сроков, необходимых для создания новой техники. В силу описанных здесь причин возможности традиционной технологии исследования динамики механических систем с ручным выводом уравнений движения резко ограничены. Альтернативой традиционной технологии динамического анализа является технология автоматизированного анализа динамики систем тел.

3. Технология автоматизированного анализа динамики механических систем

Все способы получения уравнений движения для тел механической системы основаны на законах, опубликованных Ньютоном в 1687 г, а также на работах Эйлера, Даламбера и Лагранжа, опубликованных в конце 18 века.

Развитие науки и техники, быстрое развитие ЭВМ, появившихся в 1950-х годах, стимулировали дальнейшее развитие методов механики. В 1955 году Денавит и Хартенберг разработали матричный аппарат пространственной кинематики твердых тел, который в 1965 году Уикер впервые применил к динамике. Эти работы можно рассматривать как отправную точку развития вычислительной механики. В то же время предпринимаются первые попытки применить вычислительные машины для синтеза уравнений движения системы тел. Оказалось, что непосредственный перенос алгоритмов ручного вывода на ЭВМ – идея не слишком удачная. Вычисления частных производных и производных по времени на ЭВМ трудная задача, а промежуточные выражения настолько громоздки, что для некоторых задач недостаточно ресурсов компьютеров. Потребность в эффективных алгоритмах вывода уравнений привела к развитию и переработке методов классической механики с ориентацией на использование ЭВМ. Первыми в этой области стали работы Роберсона и Виттенбурга, Вукобратовича, Шилена и Кройцера. В этих работах представлен так называемый прямой метод формирования системы уравнений движения, замечательной особенностью которого является использование соотношений, использующих только алгебраические матричные операции умножения и сложения. Прямой метод получил развитие в работах Физерстоуна, Верещагина, Айхбергера, Погорелова, результатами которых являются различные модификации более эффективных методов составных тел и отдельных тел.

Ниже приводится краткое описание двух основных способов вывода уравнений движения для систем твердых тел. Начнём с классического способа вывода уравнений движения – метода Ньютона-Эйлера

Метод Ньютона-Эйлера

При данном методе механизм рассматривается, как система из n свободных твердых тел. Для каждого тела записывается три уравнения для линейных ускорений (уравнения Ньютона) и три уравнения для угловых ускорений (уравнения Эйлера). В итоге получается 6n уравнений движения. Поскольку силы, в связях между телами системы равны по модулю и противоположны по направлению, полученных уравнений движения недостаточно для решения задачи динамики. Для определения сил, действующих между телами системы c числом p точек контакта, вводятся дополнительные уравнения связей, количество которых равно 3p. Если число контакта между двумя телами больше трех, то такая система является переопределенной и получаемая система уравнений не имеет решения.

Система уравнений движения в абсолютных координатах в сочетании с уравнениями связей имеет следующий вид:

,

где q – столбец координат тел системы (размером 6n); – матрица масс; – матрица гироскопических и центробежных сил; – уравнения связей; Cq – матрица переменных коэффициентов уравнений связей от кинематических уравнений связей размерности k  n (k – число связей);  – вектор сил реакции связей (называемых также множителями Лагранжа); F –вектор внешних сил.

Такая форма представления уравнений движения называется уравнениями в избыточных координатах, поскольку в них используется число координат, большее чем число степеней свободы рассматриваемой системы. Под степенями свободы механической системы понимается совокупность независимых координат перемещения и/или вращения тел системы, полностью определяющая их положение.

Поскольку получаемые уравнения являются линейными, они могут быть решены при помощи соответствующих алгоритмов для таких систем уравнений. При таком подходе очень просто добавлять к системе внешние и внутренние силы. Работа с таким уравнениями довольно проста, что делает данный метод идеальным для относительно небольших систем тел, содержащих не более 10 элементов. Решение системы линейных уравнений является процессом порядка 3, что означает восьмикратное увеличение вычислительных затрат при удвоении числа уравнений, поэтому данный метод является не эффективным для систем, содержащих большое число элементов.

Уравнения Лагранжа 2-го рода

Если все связи в системе являются голономными, т.е. зависят только от координат и не зависят от времени, то для получения уравнений движения можно воспользоваться уравнениями Лагранжа 2-го рода:

,

где – кинетическая энергия системы; q – столбец обобщённых координат системы (размером n); П(q,t) – потенциальная энергия системы.

Этот способ получения уравнений движения довольно прост и вычисления согласно нему могут быть выполнены вручную студентами начальных курсов.

Уравнения движения после вычисления производных имеют вид

,

где M – матрица масс системы размером n × n; Q – вектор обобщённых активных сил и сил инерции.

Такая форма представления уравнений движения называется уравнениями в минимальных координатах.

Однако составление уравнений движения механических систем с большим числом степеней свободы может оказаться очень непростой процедурой. Это связано с ростом сложности выражений для кинематических величин, определяющих положение, скорости и ускорения тел, входящих в систему, при увеличении длины кинематических цепей. Даже само применение операции дифференцирования в этом случае приводит к появлению огромных промежуточных выкладок.