16.Коррекция инструмента при непрямоугольном формообразовании.

17.Повышение языкового уровня управляющих программ. Пример.

Стандартный язык ISO-7bit не позволяет в полной мере описать требуемые режимы и геометрию деталей в связи м чем в системах ЧПУ помимо стандартных ф-ций могут применяться макроопределения готовых форм и стандартных циклов, подпрограмм пользователя, а также автоматизированная диалоговая подготовка управляющих программ.

Стандартный цикл устанавливает строго определённую посл-ность движений, параметры которых даны в тексте управляющей программы.

Фиксация некоторых пар-ов может быть выполнена разработчиком СУ либо станкостроителем при стыковке СУ с объектом. В некоторых случаях стандартные циклы могут трактоваться как подпрограммы, постоянно хранимые в устр-ве ЧПУ.

Некоторые стандартные циклы:

Готовые формы явл.принадлежностью матем. Обеспечения спец. Системой ЧПУ. Заранее готовой формы сост. Лишь в привязке к контуру детали, а её вызов может быть осуществлён путём обращения к подпрограмме по G-функции, либо указанием спец. выделенной клавишей.

Пример формы:

При многократном выполнении определённых действий часть упр. Программы может быть вынесена в виде подпрограммы.

Вызов подпрограммы осуществляется командой L с указанием 5-тиразрядного кода. 3 старших разряда указывают номер подпрограммы, а младшие 2 разряда – число повторений подпрограммы. В подпрограммах целесообразно использование относительной системы отсчёта, не привязываясь к базовой системе координат станка. Использование абсолютной системы отсчёта требует внесение корректировок в систему координат станка.

Макроязык пользователя расп. след возможностями:

1)манипуляции с с пар-рами, организация условных и безусловных переходов

2)Доступ к входным цифровым регистрам СУ с послед. Обработкой воспринимаемых сигналов.

3)Формирование любых пользовательских сообщений на экране дисплея.

18.Программирование на основе стандарта step-nc

Для реализации всех возможностей CAD-CAM систем, на смену старому стандарту пришёл новый: STEP-NC, а именно ИСО14649. Стандарт STEP-NC предлагает модель того, что необходимо выполнить. При этом подробности того, как это выполнить решаются самой системой ЧПУ.

Стандарт ИСО14649 устанавливает 9 компонентов функциональности:

1. Проект

2. Изделие

3. Типовая форма

4. Исполняемый блок

5. Переход

6. Траектория инструмента

7. Измерения

Примером языка на основе стандарта явл. Объектно-ориентированный язык EXPRESS. В таком языке форма детали определяется путём набора типовых форм технологич. переходов.

Структура управл. Программы на EXPRESS:

Я дро модели СТЕП-НС составляет план операции, который явл. Послед шагов операции. Каждый шаг операции связан с переходом выполняемым в некоторой типовой форме изделия. В свою очередь переход содержит технологич. Алгоритм и указания по настройке. Задание типовых форм произв в след виде:

19.Интерполяторы. Типы интерполяторов.

20.Аппроксимация нелинейных участков траектории рабочего органа.

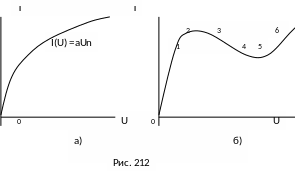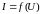В ольтамперные характеристики нелинейных элементов на практике чаще всего получают экспериментальным путем и представляют их или в графиче­ской форме [в виде графической диаграммы функции ], или в таблич­ной форме [в виде таблицы координат точек функции 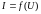]. При аналити­ческих методах расчета нелинейных цепей к ВАХ предъявляются требования, чтобы они были представлены в аналитической форме, т.е. в виде аналитиче­ского выражения.Под аппроксимацией ВАХ понимают замену ее графической или таблич­ной формы на аналитическую. К уравнению аппроксимации предъявляются два противоречивых требования. Во-первых, уравнение аппроксимации должно по возможности точно описывать заданную ВАХ. Для более полного выполнения этого требования необходимо усложнять структуру этого уравнения. Во-вто­рых, уравнение аппроксимации, будучи введенным в систему уравнений Кирх­гофа, должно позволять решение этой системы доступными методами. Для вы­полнения этого требования структура этого уравнения должна быть по возмож­ности более простой. Таким образом, при выборе уравнения аппроксимации всегда приходится принимать компромиссное решение между этими двумя тре­бованиями.Различают два способа аппроксимации нелинейных ВАХ – полная и ку­сочная (по частям).В простейших случаях при монотонном характере изменения функции I(U) ВАХ может быть аппроксимирована полностью одним нелинейным урав­нением (рис. 212а).

В более сложных случаях, когда функция I(U) имеет несколько максиму­мов и минимумов, полная аппроксимация ВАХ одним уравнением становится проблематичной и нерациональной. В таких случаях применяют кусочную ап­проксимацию. Суть ее состоит в том, что вся ВАХ разбивается по тому или дру­гому принципу на отдельные участки (куски) (рис. 212б). Отдельные участки ап­проксимируются однотипными, но простыми по структуре, уравнениями, коэф­фициенты в которых изменяются при переходе от одного участка к другому. Если отдельные участки ВАХ аппроксимируются отрезками прямой 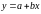, то такая аппроксимация получила название кусочно-линейной. Если отдельные участки ВАХ аппроксимируются квадратичной (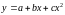 ) или кубической ( ) параболой, то отдельные участки получили название сплайнов, а сама аппроксимация – аппроксимации сплайнами. Кусочная ап­проксимация позволяет получить высокую степень приближения к заданной ВАХ, однако требует большого числа однотипных расчетов при определении коэффициентов в уравнениях аппроксимации.

Кусочная аппроксимация широко применяется при расчете нелинейных цепей на ЭВМ.

21.Линейный интерполятор по методу оценочной функции (МОФ). Пример.Уравнение отрезка прямой, производимой системой ЧПУ, можно записать в виде. Где xi,

yi –точки, лежащие на прямой, а Δx, Δy - приращения

x_i Δy= y_iΔx

x_i Δy- y_iΔx=0

Если это уравнение приравнять к некоторой функции, то получим:

F=x_i Δy- y_iΔx, из этого уравнения видно, что если функция равно 0, то точка расположена на прямой, если функция больше 0, то точка над прямой, если функция меньше 0, то точка под прямой. Таким образом, оценка функции по уравнению позволяет разработать алгоритм оценочной функции, при котором с определенной частотой анализируется знак оценочной функции.

В зависимости от знака выдается единичное приращение по соотв. Координате, масштаб приращения по каждой координате принимается равным дискретности шага этой координате F=y_iΔx -x_i Δy.

Начало производимого участка совмещается с началом координат и определив знак оценочной функции, выдается шаг по координате x (F>=0) или по координате y (F<0), после чего вновь определяется знак оценочной функции и делается приращение по соотв. Координате. Этот процесс по вторяется до тех пор, пока значение координат и будет соотв. конечной точке участка прямой.

F_i+1=Fi+Δx- выражение для оц. Функции в случае

единичного шага по х

- АЛГОРИТМ

Пример – расчет траектории движения рабочего органа по методу оц функции, управляющие импульсы по большей координате выдаются в каждый интервал времени, а импульсы по меньшей координате – в зависимости от значения оценочной функции.