27.Алгоритм создания упорядоченного бинарного дерева.

Упорядоченнымназывается дерево, в котором для каждого узлаNзначение левого дочернего узла меньше, чем значение вN, а значение правого дочернего узла больше значения вN. Если в дереве могут содержаться одинаковые значения, то программист должен самостоятельно определить, влево или вправо помещать значение, равное значению в родительском узле (строгое неравенство заменить на нестрогое).

Построение упорядоченного дерева начинается с корня. Первое входящее значение помещается в корень дерева. Для последующих значений производиться сравнение со значением в очередном узле, начиная с корня. Если оно меньше (или равно) значению в узле, то переходим в левое поддерево, иначе – в правое. Эти переходы и сравнения продолжаются до тех пор, пока мы не придем к ссылке, которая равна nil. Тогда создается новый узел, заполняются его поля: информационное - новым значением, ссылки на левое и правое поддеревья пустым значениеnil. Адрес нового узла передается в одно из ссылочных полей родительского узла. Для этого необходимо воспользоваться параметром-переменной. Этот алгоритм реализован в виде рекурсивной процедурыInsert.

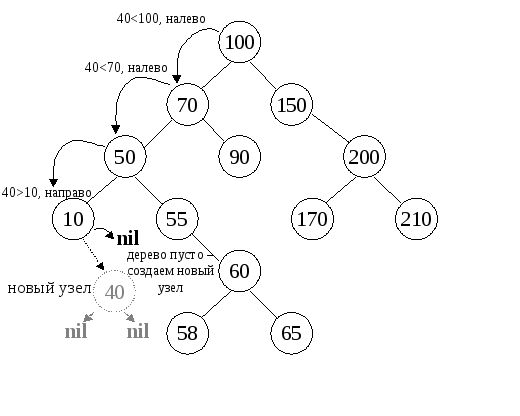
Рис.2 Добавление нового узла в упорядоченное дерево.

Листинг процедуры добавления нового узла в упорядоченное дерево.

{Параметры процедуры: Tree– указатель на корень дерева,NewValue– значение для добавляемого узла.}

ProcedureInsert(varTree:PTree; NewValue:integer);

varTemp:PTree;

begin

if Tree = nil then begin

new(Tree); // создание нового узла, в том числе и корневого

Tree^.inf:=NewValue; Tree^.Left:=nil; Tree^.Right:=nil; // заполнение полей

end

else

ifNewValue <=Tree^.infthen

Insert(Tree^.left,NewValue)

{переход к левому поддереву}

else

Insert(Tree^.Right,NewValue)

{переход к правому поддереву}

end;

Следует отметить, что в процедуре InsetrпараметрTreeпередается как параметр-переменная, а не как параметр-значение в процедуреPrintTree. Это очень важно, так как в случае включения нового узла параметру-переменнойTreeприсваивается адрес нового узла и через нее передает в родительский узел ссылкы (адрес) на включенный узел, изменяя старое значение равноеnil.Само по себе создание бинарного дерева тривиально. В простейшем случае корневой узел бинарного дерева определяет все бинарное дерево. В программе необходимо описать указатель на корень дерева (например, var Root:PTree;). В начале программы необходимо провести инициализацию бинарного дерева – указателю на корень присвоить пустое значение (Root:=nil;). Бинарного дерева не существует, поэтому это пустое значение служит начальным значением бинарного дерева. Добавление новых элементов в дерево будем осуществлять процедурой Insert. Например, добавление числа Х в бинарное дерево будет выглядеть так: Insert(Root,X). Вывод на экран содержимого дерева можно записать процедурой PrintTree(Root).

Если построено упорядоченное дерево, то его можно применять для сортировки данных. Осуществляя обход дерева InOrderможно получить значения узлов в порядке возрастания, т.е. отсортированную последовательность. Для вывода значений узлов в порядке убывания необходимо внести небольшие изменения в процедуру обхода – поменять местами обходы левого и правого поддеревьев:

ProcedurePrintTree1(Tree: PTree); // InOrder

begin

if Tree<>nil then begin // если дерево не пустое, то

PrintTree1(Tree^.Right); //обходправого поддерева

Writeln(‘Value = ‘,Tree^.inf); // обработать узел

PrintTree1(Tree^.Left); // обход левого поддерева

end;

end;