Группа: определение и примеры групп
Множество
GG
с алгебраической операцией
∗∗
называется группой, если выполняются следующие условия:
1) операция
∗∗
в
GG
ассоциативна:
a∗(b∗c)=(a∗b)∗c ∀a,b∈Ga∗(b∗c)=(a∗b)∗c ∀a,b∈G
;
2) в
GG
существует нейтральный элемент
θ:a∗θ=θ∗a=a ∀a∈Gθ:a∗θ=θ∗a=a ∀a∈G
;
3) для каждого элемента
a∈Ga∈G
существует обратный ему элемент
a−1∈G:a∗a−1=a−1∗a=θa−1∈G:a∗a−1=a−1∗a=θ
.
Если операция
∗∗
коммутативна, то группа называется коммутативной, или абелевой. В противном случае группа называется некоммутативной.
Относительно операции сложения группами являются множества
Z, Q, RZ, Q, R
. Относительно операции умножения группами являются множества
Q∖{0}Q∖{0}
и
R∖{0}R∖{0}
отличных от нуля рациональных и действительных чисел, поскольку для нуля не существует обратного элемента. Все эти группы коммутативные.
В группах по сложению нейтральный элемент
θθ
называют нулевым (или просто нулем), а обратный элемент
a−1a−1
— противоположным
(−a)(−a)
. В группах по умножению нейтральный элемент
θθ
называют единичным (или просто единицей) и обозначают
ee
, для обратного элемента
a−1a−1
название и обозначение сохраняется.
Пример В.4. Доказать, что множество
{0}{0}
, состоящее из одного числа нуль, образует коммутативную группу по сложению.
Решение. Действительно, операция сложения определена на указанном множестве, так как
0+0=00+0=0
. Из этого равенства следует, что этот единственный элемент множества служит нулевым (нейтральным) элементом, а также противоположным (обратным) для себя. Ассоциативность сложения очевидна:
(0+0)+0=0+(0+0)(0+0)+0=0+(0+0)
. Следовательно, все (три) условия в определении группы выполняются. Учитывая коммутативность сложения, заключаем, что рассматриваемое множество — коммутативная группа.
Кольцо
Множество
KK
, на котором заданы две операции — сложение
(+)(+)
и умножение
(⋅)(⋅)
, называется кольцом, если выполняются следующие условия:
1) относительно операции сложения множество
KK
— коммутативная группа, т.е.
а) операция сложения коммутативна:
a+b=b+a ∀a,b∈Ka+b=b+a ∀a,b∈K
;
б) операция сложения ассоциативна:
a+(b+c)=(a+b)+c ∀a,b,c∈Ka+(b+c)=(a+b)+c ∀a,b,c∈K
;
в) существует нулевой элемент
θ:a+θ=θ+a=a ∀a∈Kθ:a+θ=θ+a=a ∀a∈K
;
г) для каждого элемента
a∈Ka∈K
существует противоположный ему элемент
(−a)∈K:a+(−a)=(−a)+a=θ(−a)∈K:a+(−a)=(−a)+a=θ
;
2) операция умножения в множестве
KK
ассоциативна:
a⋅(b⋅c)=(a⋅b)⋅c∀a∈K,∀b∈K,∀c∈K;a⋅(b⋅c)=(a⋅b)⋅c∀a∈K,∀b∈K,∀c∈K;
3) операции сложения и умножения связаны законами дистрибутивности:
(a+b)⋅c=a⋅c+b⋅c,c⋅(a+b)=c⋅a+c⋅b∀a∈K,∀b∈K,∀c∈K;(a+b)⋅c=a⋅c+b⋅c,c⋅(a+b)=c⋅a+c⋅b∀a∈K,∀b∈K,∀c∈K;
Если операция умножения коммутативна:
a⋅b=b⋅aa⋅b=b⋅a
, то кольцо называется коммутативным, в противном случае кольцо называется некоммутативным. Если для операции умножения существует единичный элемент
e:a⋅e=e⋅a=ae:a⋅e=e⋅a=a
, то говорят, что кольцо
KK
— есть кольцо с единицей.
Кольцами являются множества целых, рациональных, действительных чисел, причем все они — коммутативные кольца с единицей. Примеры других колец, в том числе и некоммутативных, встретятся в дальнейшем. Как видим, кольцо — это множество, в котором определены три операции: сложение, умножение и вычитание.
Рассмотрим подробнее законы дистрибутивности. Пусть на множестве
KK
заданы две операции
⊕⊕
и
⊗⊗
. Операция
⊗⊗
называется дистрибутивной слева относительно операции
⊕⊕
, если для любых
a,b,ca,b,c
из
KK
справедливо равенство:
c⊗(a⊕b)=(c⊗a)⊕(c⊗b),c⊗(a⊕b)=(c⊗a)⊕(c⊗b),
и дистрибутивной справа относительно операции
⊗⊗
, если для любых
a,b,ca,b,c
из
KK
справедливо равенство:
(a⊕b)⊗c=(a⊗c)⊕(b⊗c).(a⊕b)⊗c=(a⊗c)⊕(b⊗c).
Если операция
⊗⊗
коммутативна, то дистрибутивность слева операции
⊗⊗
относительно операции
⊕⊕
влечет дистрибутивность справа, так как
(a⊕b)⊗c=c⊗(a⊕b)=(c⊗a)⊕(c⊗b)=(a⊗c)⊕(b⊗c).(a⊕b)⊗c=c⊗(a⊕b)=(c⊗a)⊕(c⊗b)=(a⊗c)⊕(b⊗c).
В этом случае говорят, что операция
⊗⊗
дистрибутивна относительно операции
⊕⊕
. Например, операция умножения чисел дистрибутивна (слева и справа) относительно операции сложения чисел. Следующий пример показывает, что имеются операции с "односторонней" дистрибутивностью.
Пример В.6. Рассмотрим множество
R+R+
положительных действительных чисел. На этом множестве определим две операции: умножения
(×b)(×b)
и возведения в положительную степень
(a↑b=ab)(a↑b=ab)
. Доказать, что операция
↑↑
возведения в степень дистрибутивна справа относительно умножения, но не дистрибутивна слева.
Определение 1. Эйлеровым путем в графе называется путь, содержащий все ребра графа и проходящий через каждое по одному разу.
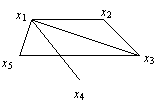
Пример 1. Рассмотрим граф
|
|
|
|
Он имеет эйлеров путь (x4, x1, x3, x2, x1, x5, x3).
Определение 2. Эйлеровым циклом в графе называется цикл, содержащий все ребра графа и проходящий через каждое по одному разу.
Определение 3. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
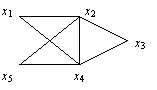
Пример 2. Рассмотрим граф
|
|
|
|
Данный граф является эйлеровым, так как он имеет эйлеров цикл (x2, x5, x4, x1, x2, x3, x4, x2).
Теорема 1. Эйлеров граф связный, и все его вершины четны.
Доказательство.
Связность следует из определения эйлерового графа. Эйлеров цикл содержит каждое ребро и притом только один раз. Следовательно, степень каждой вершины графа должна состоять из двух одинаковых слагаемых: количество входов в вершину и количество выходов из вершины.
Теорема 2. Если граф G(X,T) связный и все его вершины четны, то он обладает эйлеровым циклом.
Теорема 3. Если граф G(X,T) обладает эйлеровым путем с концами А и В, то граф G(X,T) связный и А и В его единственные нечетные вершины.
Доказательство.
Если путь начинается в А и кончается в В, то А и В нечетные вершины, даже если путь неоднократно проходил через них. В любую другую вершину путь должен привести и вывести из нее, т.е. остальные вершины четные.
Теорема 4. Если граф G(X,T) связный и А и В его единственные нечетные вершины, то граф обладает эйлеровым путем с концами А и В.
Теорема 5. Если граф G(X,T) связный, то можно построить цикличный маршрут, содержащий все ребра в точности 2 раза, по одному в каждом направлении.
Удаление ребра или удаление дуги. Если ai - дуга графа G = (X, A), то G-ai – подграф графа G, получающийся после удаления из G дуги ai . Заметим, что концевые вершины дуги ai не удаляются. Удаление из графа множества вершин или дуг определяется как последовательное удаление определенных вершин или дуг. Удаление дуг a4 и a7 показано на рис. 2.3,в. Результирующая матрица смежности графа после выполнения операции удаления дуги ai получается путем удаления соответствующих элементов из исходной матрицы ( таблица 2.1в).
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Замыкание или отождествление. Говорят, что пара вершин хi и xj в графе G замыкается (или отождествляется), если они заменяются такой новой вершиной, что все дуги в графе G, инцидентные хi и xj , становятся инцидентными новой вершине. Например, результат замыкания вершины х1 и х2 показан на рис. 2.3,г для графа G ( рис. 2.3,а). Матрица смежности графа после выполнения операции замыкания вершин хi и xj получается путем поэлементного логического сложения i - го и j - го столбцов и i -ой и j - строк в исходной матрице и "сжимания" матрицы по вертикали и горизонтали ( таблица 2.1г).
Стягивание. Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин. Граф, изображенный на рис. 2.3,д получен стягиванием дуги a1 , а на рис. 2.3,е – стягиванием дуг a1 , a6 и a7 . Соответствующие результирующие матрицы смежности показаны в таблицах 2.1д и 2.1е.