Тема 3. Пропускная способность транспортной сети

Если пропускная способность таких элементов, как остановочный пункт, зависит в основном от величины пассажирообмена, то пропускная способность транспортных узлов зависит от многих факторов, таких как:

- количество пересекающихся направлений;

- интенсивность и состав транспортных потоков на отдельных направлениях;

- конфигурация пересечений;

- системы регулирования и организации движения на пересечениях;

- интенсивность пешеходного движения;

- ширина проезжей части;

- состояние дорожного покрытия, погодных условий и т.д.

Пропускная способность линий массового транспорта в основном зависит от пропускной способности остановочных пунктов, поэтому при расчете пропускной способности линий массового транспорта их прежде всего оценивают по этому признаку, с дальнейшей проверкой сложности транспортных узлов и пересечений.

Минимально допустимый интервал движения определяет максимальное количество транспортных средств общественного транспорта, которое может пропустить линия (составляет примерно около 2-х минут):

 . (8)

Наибольшую пропускную способность имеет прямоугольная схема, поскольку характеризуется наиболее простыми пересечениями в транспортных узлах, наличием достаточного количества дублирующих магистралей, возможностью проезда различными маршрутами.

Наименьшую пропускную способность имеет радиальная схема, поскольку дублирующих магистралей нет, все транспортные потоки сходятся в одном пересечении.

Радиально-кольцевая и треугольная схема занимают промежуточное положение по пропускной способности, а в комбинированной схеме многое зависит от того, насколько удачно сочетаются отдельные ее элементы, и пропускная способность приближается к пропускной способности прямоугольной схемы.

Теоретическую пропускную способность транспортной линии определяют по формуле:

 , (9)

где V_∂ – скорость транспортного потока (скорость наиболее тихоходного транспортного средства), км/ч;

t_p – время реакции водителя, с;

в – величина замедления при торможении м²/с;

l – длина транспортного средства, м;

l₀ – дистанция безопасности, м.

При расчете фактической пропускной способности необходимо учитывать ряд факторов, влияющих на пропускную способность транспортной линии, таких как:

- состав транспортного потока;

- количество остановочных пунктов массового транспорта на линии;

- количество пересечений в одном уровне;

- количество пешеходных переходов;

- состояние и тип дорожного покрытия;

- метеорологические условия;

- характер продольного профиля и т.д.

Поэтому в реальных условиях расчеты пропускной способности носят приближенный характер.

Для линий массового транспорта большое значение для определения пропускной способности имеет правильный расчет времени простоя на остановочных пунктах и пересечениях в одном уровне.

Для безрельсового транспорта, двигающегося в транспортном потоке, фактическая пропускная способность будет всегда меньше теоретической, что вызвано необходимостью совершать перестроения, обгон, объезд стоящих транспортных средств (т.е. маневрировать).

Пропускная способность остановочного пункта массового транспорта определяется, исходя из продолжительности его занятия транспортным средством:

N_o =   , (10)

где Т_о – продолжительность занятия остановочного пункта транспортным средством, с.

Т_о = t₁ + t₂ + t₃ + t₄ , (11)

где t₁ – затраты времени на маневрирование при подъезде к остановочному пункту, с;

t₂ – затраты времени на посадку и высадку пассажиров, с;

t₃ – затраты времени на подачу сигнала и закрытие дверей, с (в расчётах 3 с.);

t₄ – затраты времени на освобождение остановочного пункта, с.

 , (12)

 , (13)

 , (14)

где Δ – доля пассажиров, осуществляющих посадку и высадку на данном остановочном пункте от номинальной вместимости транспортного средства;

q – номинальная вместимость, пасс.;

t’ – затраты времени на посадку, высадку 1 пассажира (зависят от типа транспортного средства, оборудования остановочного пункта), с;

n_d – количество дверей;

ε – коэффициент неравномерности распределения пассажиров между дверьми автобусов;

a – величина ускорения при разгоне, м²/с.

Таким образом, пропускная способность остановочного пункта зависит в основном от состава подходящего транспортного потока, пассажирообмена и длины кармана.

Гамильтоновы циклы

Название «гамильтонов цикл» произошло от задачи «Кругосветное путешест-вие», придуманной Гамильтоном1 в XIX веке: нужно обойти все вершины графа,диаграмма которого показана на рис. 10.6 (в исходной формулировке верши-

ны были помечены названиями столиц различных стран), по одному разу и вернуться в исходную точку. Этот граф представляет собой укладку додекаэдра.

10.3.1. Гамильтоновы графы

Если граф имеет простой цикл, содержащий все вершины графа (по одномуразу), то такой цикл называется гамилътоновым циклом, а граф называется га-милътоновым графом.

Гамильтонов цикл пе обязательно содержит все рёбра графа. Ясно, что гамиль-топовым может быть только связный граф.

З А М Е Ч А Н И ЕЛюбой граф G можно превратить в гамильтонов, добавив достаточное количество новыхвершин и инцидентных им рёбер и не добавляя рёбер, инцидентных только старым вер-шинам. Для этого, например, достаточно к вершинам v\,...,vv графа G добавить вершиныmi, ... ,ир и множество рёбер {(г>г,иг)} и {(и*,i>i+i)}-Простые необходимые и достаточные условия гамильтоновости графа неизвест-ны. Известны только некоторые достаточные условия, одно из которых приве-дено в следующей теореме.

ТЕОРЕМА Если 6{G) ^ р/2, то граф G является гамилътоновым.ДОКАЗАТЕЛЬСТВО ОТ противного. Пусть G — пе гамильтонов. Добавим к G мини-мальное количество новых вершин и\,...,ип, соединяя их со всеми вершинамиG так, чтобы граф G' : = G + и\ + Ь ип был гамильтоновым.Пусть v,ui,w,... ,v — гамильтонов цикл в графе Gпричём v е G, щ е G',

и\ $ G. Такая пара вершин v и щ в гамильтоиовом цикле обязательно найдется,иначе граф G был бы гамильтоновым. Тогда w 6 G, w 0 {щ,... ,ип}, иначевершина щ была бы не нужна. Более того, вершина v не смежна с вершиной w,

иначе вершина и\ была бы не нужна. Далее, если в цикле v, ui, w,..., v', w',..., vесть вершина w', смежная с вершиной w, то вершина v' не смежна с вершинойv, так как иначе можно было бы построить гамильтонов цикл v, v',..., w, w'... vбез вершины щ, взяв последовательность вершин w,... ,v' в обратном порядке.Отсюда следует, что число вершин графа G', не смежных с v, не менее числавершин, смежных с w. Но для любой вершины w графа G d(w) ^ р/2 + п попостроению, в том числе d(v) ^ р/2 + п. Общее число вершин (смежных и несмежных с v, за исключением самой вершины v) составляет п + р — 1. Такимобразом, имеем:п + р- 1 = d(v) + d(v) ^ d(w) + d(v) = +Следовательно, 0 ^ п + 1, что противоречит тому, что п > 0. •

10.3.2. Задача коммивояжёра

Рассмотрим следующую задачу, известную как задача коммивояжёра. Имеется ргородов, расстояния между которыми известны. Коммивояжёр должен посетитьвсе р городов по одному разу, вернувшись в тот, с которого начал. Требуется

найти такой маршрут движения, при котором суммарное пройденное расстояниебудет минимальным.

Очевидно, что задача коммивояжёра — это задача отыскания кратчайшего га-мильтоиова цикла в нагруженном полном графе.

Можно предложить следующую простую схему решения задачи коммивояжёра:сгенерировать все р\ возможных перестановок вершин полного графа, подсчи-тать для каждой перестановки длину маршрута и выбрать из них кратчайший.Очевидно, такое вычисление потребует не менее 0(р\) шагов.Как известно, р\ — быстро растущая функция. Таким образом, решение задачи коммивояжёра описанным методом полного перебора оказывается практическинеосуществимым даже для сравнительно небольших р. Более того, известно, чтозадача коммивояжёра принадлежит к числу так называемых NP-полных задач,

подробное обсуждение которых выходит за рамки этого учебника.Вкратце суть проблемы ./VP-полноты сводится к следующему. В различных об-ластях дискретной математики, комбинаторики, логики и т. п. известно мно-

жество задач, принадлежащих к числу наиболее фундаментальных, для кото-рых, несмотря на все усилия, не удалось найти алгоритмов решения, имеющихполиномиальную сложность. Более того, если бы удалось отыскать эффектив-10.4. Независимые и покрывающие множества 345ный алгоритм решения хотя бы одной из этих задач, то из этого немедленноследовало бы существование эффективных алгоритмов для всех остальных задачданного класса. На этом основано общепринятое мнение, что таких алгоритмов

пе существует.ОТСТУПЛЕНИЕ

Полезно сопоставить задачи отыскания эйлеровых и гамильтоновых циклов, рассмотрен-ные в этом и предыдущем разделах. Внешнеформулировки этих задач очень похожи,однако они оказываются принципиально различными с точки зрения практического при-

менения. Уже давно Эйлером получено просто проверяемое необходимое и достаточноеусловие существования в графе эйлерова цикла. Что касается гамильтоновых графов, то ля них неизвестны простые необходимые и достаточные условия. На основе необходимо-

го и достаточного условия существования эйлерова цикла можно построить эффективныеалгоритмы отыскания такого цикла. В то же время задача проверки существования га-мильтопова цикла оказывается ./VP-полной (так же как и задача коммивояжёра). Далее,

известно, что почти нет эйлеровых графов, и эффективный алгоритм отыскания эйле-ровых циклов редко оказывается применимым на практике. С другой стороны, можнопоказать, что почти все графы — гамильтоновы, то естьоо |S(p)|

где 'Kip) — множество гамильтоновых графов с р вершинами, a S(р) — множество всехграфов с р вершинами. Таким образом, задача отыскания гамильтонова цикла или за-дача коммивояжёра являются практически востребованными, по эффективный алгоритм

решеиия для них неизвестен (и, скорее всего, пе существует).__

Диаграмма Гантта

Пример диаграммы Ганта

Диагра́мма Га́нта (англ. Gantt chart, также ленточная диаграмма, график Ганта) — это популярный типстолбчатых диаграмм, который используется для иллюстрации плана, графика работ по какому-либопроекту. Является одним из методов планирования проектов.

Первый формат диаграммы был разработан Генри Л. Гантом (Henry L. Gantt, 1861‒1919) в 1910 году.

Диаграмма Ганта представляет собой отрезки (графические плашки), размещенные на горизонтальнойшкале времени. Каждый отрезок соответствует отдельной задаче или подзадаче. Задачи и подзадачи, составляющие план, размещаются по вертикали. Начало, конец и длина отрезка на шкале временисоответствуют началу, концу и длительности задачи. На некоторых диаграммах Ганта также показываетсязависимость между задачами. Диаграмма может использоваться для представления текущего состояниявыполнения работ: часть прямоугольника, отвечающего задаче, заштриховывается, отмечая процентвыполнения задачи; показывается вертикальная линия, отвечающая моменту «сегодня».

Часто диаграмма Ганта соседствует с таблицей со списком работ, строки которой соответствуют отдельновзятой задаче, отображенной на диаграмме, а столбцы содержат дополнительную информацию о задаче. Пример такой таблицы представлен ниже.

Список работ	продолжительность работы	стоимость
покупка здания	1.02.08—8.02.08	15000 $
регистрация предприятия	2 8.02.08—18.02.08	3 884 лея

Алгоритм Краскала

Следующий алгоритм, известный как алгоритм Краскала, находит кратчайший

остов в связном графе.

Алгоритм 9.12 Алгоритм Краскала

Вход: список Е рёбер графа G с длинами, упорядоченный в порядке возрастания

длин.

Выход: множество Т рёбер кратчайшего остова.

Т: = 0

к: = 1 { номер рассматриваемого ребра }

for г from 1 to р - 1 do

while z(T + E[k}) > 0 do

к : = к + 1 { пропустить это ребро }

end while

Т: = Т + Е[к] { добавить это ребро в SST }

к: = к + 1 { и исключить его из рассмотрения }

end for

ОБОСНОВАНИЕ ДЛЯ обоснования алгоритма Краскала достаточно показать, что

выдерживается схема алгоритма предыдущего подраздела. Действительно, по-

скольку в множестве рёбер Т нет циклов по построению, это множество суть

совокупность рёбер некоторого множества деревьев. Если множество Т содержит

более одного дерева, то существует ребро, при добавлении которого не возникает

цикла — оно соединяет два дерева в Т. Добавляемое ребро — кратчайшее воз-

можное, зиачит, на нём реализуется расстояние между некоторыми деревьями в

Т. По построению в конце работы алгоритма множество рёбер Т содержит р— 1

элемент, а значит, является искомым остовом. •

З А М Е Ч А Н И Е

Исследование алгоритма Краскала дало толчок развитию теории жадных алгоритмов,

см. 2.6.

ТЕОРЕМА Семейство всех таких подмножеств множества рёбер графа, которые

не содержат циклов, является матроидом.

330 Глава 9. Деревья

ДОКАЗАТЕЛЬСТВО Пустое множество рёбер пе содержит циклов и аксиома М\

(см. 2.6.1) выполнена. Далее, если множество рёбер не содержит циклов, то лю-

бое его подмножество также не содержит циклов, и аксиома М2 выполнена. Пусть

теперь Е' С Е — произвольное множество рёбер, a G' — правильный подграф

графа G, образованный этими рёбрами. Очевидно, что любое максимальное не

содержащее циклов подмножество множества Е' является объединением осто-

вов компонент связности графа G' и по теореме 9.1.2 содержит p(G') - k(G')

элементов. Таким образом, все максимальные не содержащие циклов подмно-

жества произвольного множества рёбер содержат одинаковое количество эле-

ментов, и по теореме 2.6.2 семейство ациклических подмножеств рёбер образует

матроид. •

Таким образом, алгоритм Краскала как жадный алгоритм (см. 2.6.4), применён-

ный к матроиду, находит ациклическое подмножество рёбер наименьшего веса.

По построению алгоритма (основной цикл до р — 1) это подмножество рёбер

древочисленно, а значит, является кратчайшим остовом.__

Эйлеровой цепью в неориентированном графе G называется простая цепь, содержащая все ребра графа G. Эйлеровым циклом называется замкнутая Эйлерова цепь. Аналогично, эйлеров путь в орграфе G — это простой путь, содержащий все дуги графа G. Эйлеров контур в орграфе G — это замкнутый эйлеров путь. Граф, в котором существует эйлеров цикл, называется эйлеровым..

Простой критерий существования эйлерова цикла в связном графе дается следующей теоремой.

Теорема 7.1. (Эйлер) Эйлеров цикл в связном неориентированном графе G(X, E) существует только тогда, когда все его вершины имеют четную степень.

Доказательство.

Необходимость. Пусть μ - эйлеров цикл в связном графе G, x — произвольная вершина этого графа. Через вершину x эйлеров цикл проходит некоторое количество k (k≥1) раз, причем каждое прохождение, очевидно, включает два ребра, и степень этой вершины равна 2k, т.е. четна, так как x выбрана произвольно, то все вершины в графе G имеют четную степень.

Достаточность. Воспользуемся индукцией по числу m ребер графа. Эйлеровы циклы для обычных (не псевдо) графов можно построить начиная с m=3.Легко проверить, что единственный граф с m=3, имеющий все вершины с четными степенями, есть граф K₃ (рис. 7.2). Существование эйлерова цикла в нем очевидно. Таким образом, для m=3 достаточность условий доказываемой теоремы имеет место. Пусть теперь граф G имеет m>3 ребер, и пусть утверждение справедливо для всех связных графов, имеющих меньше, чем m ребер. Зафиксируем произвольную вершину a графа G и будем искать простой цикл, идущий из a в a. Пусть μ(a, x) — простая цепь, идущая из a в некоторую вершину x. Если x ≠ a, то цепь μ можно продолжить из вершины x в некотором направлении. Через некоторое число таких продолжений мы придем в вершину z∈X, из которой нельзя продлить полученную простую цепь. Легко видеть, что z = a так как из всех остальных вершин цепь может выйти (четные степени!); a в a она начиналась. Таким образом, нами построен цикл μ, идущий из a в a. Предположим, что построенный простой цикл не содержит всех ребер графа G. Удалим ребра, входящие в цикл μ, из графа G и рассмотрим полученный граф  . В графе   все вершины имеют четные степени. Пусть   — компоненты связности графа  , содержащие хотя бы по одному ребру. Согласно предположению индукции все эти компоненты обладают эйлеровыми циклами μ₁, μ₁, …, μ_kсоответственно. Так как граф G связан, то цепь μ встречает каждую из компонент . Пусть первые встречи цикла μ с компонентами   происходят соответственно в вершинах x₁, x₂, …, x_k. Тогда простая цепь ν(a, a)=μ(a, x₁) ∪ μ₁(x₁, x₁) ∪ μ(x₁, x₂) ∪…∪ μ_k(x_k, x_k) ∪ μ(x_k, a) является эйлеровым циклом в графе G. Теорема доказана.

 

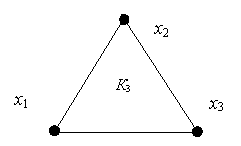
Рисунок 7.2

 

Замечание. Очевидно, что приведенное доказательство будет верно и для псевдографов, содержащих петли и кратные ребра (см. рис. 7.1,а).

Таким образом, задача о кенигсбергских мостах не имеет решения, так как соответствующий граф (см. рис. 7.1,б) не имеет эйлерова цикла из-за нечетности степеней все вершин.

Отметим, что из существования эйлерова цикла в неориентированном графе G не следует связность этого графа. Например, неориентированный граф G на рис. 7. 3 обладает эйлеровым циклом и вместе с тем несвязен.

 

Рисунок 7.3

 

Совершенно также, как теорема 7.1, могут быть доказаны следующие два утверждения.

Теорема 7.2. Связный неориентированный граф G обладает эйлеровой цепью тогда и только тогда, когда число вершин нечетной степени в нем равно 0 или 2, причем если это число равно нулю, то эйлерова цепь будет являться и циклом.

Теорема 7.3. Сильно связный орграф G(X, E) обладает эйлеровым контуром тогда и только тогда, когда для любой вершины x∈X выполняется

.

Можно также обобщить задачу, которую решал Эйлер следующим образом. Будем говорить что множество не пересекающихся по ребрам простых цепей  графа G покрывает его, если все ребра графа G включены в цепи μ_i. Нужно найти наименьшее количество таких цепей, которыми можно покрыть заданный граф G.

Если граф G — эйлеров, то очевидно, что это число равно 1. Пусть теперь G не является эйлеровым графом. Обозначим через k число его вершин нечетной степени. По теореме … k четно. Очевидно, что каждая вершина нечетной степени должна быть концом хотя бы одной из покрывающих G цепей μ_i. Следовательно, таких цепей будет не менее чем k/2. С другой стороны, таким количеством цепей граф G покрыть можно. Чтобы убедиться в этом, расширим G до нового графа  , добавив k/2 ребер  , соединяющих различные пары вершин нечетной степени. Тогда   оказывается эйлеровым графом и имеет эйлеров цикл  . После удаления из   ребер F  граф разложится на k/2 цепей, покрывающих G. Таким образом, доказана

Теорема 7.4. Пусть G — связный граф с k>0 вершинами нечетной степени. Тогда минимальное число непересекающихся по ребрам простых цепей, покрывающих G, равно k/2.

 

Алгоритм построения эйлерова цикла.

Для начала отметим, что теорема 7.1 также дает метод построения эйлерова цикла. Здесь мы рассмотрим несколько иной алгоритм.

Пусть G(X, E) — связный неорентированный граф, не имеющий вершин нечетной степени. Назовем мостом такое ребро, удаление которого из связного графа разбивает этот граф на две компоненты связности, имеющие хотя бы по одному ребру.

1°. Пусть a — произвольная вершина графа G. Возьмем любое ребро e₁=(a, x₁) , инцидентное вершине a, и положим μ = {e₁}.

2°. Рассмотрим подграф G₁(X, E\μ₁). Возьмем в качестве e₂ ребро, инцидентное вершине x₁ и неинцидентное вершине a, которое также не является мостом в подграфе G₁ (если такое ребро e₂ существует!). Получим простую цепь μ₂ = {e₁, e₂}.

3°. Пусть e₂ = (x₁, x₂), x ≠ a. Рассмотрим подграф G₂(X, E\μ₂) и удалим из него все изолированные вершины. В полученном подграфе   выберем ребро e₃∈E\μ₂, инцидентное вершине a, которое не является мостом в подграфе   (если такое ребро e₃ существует!). Получим простую цепь

μ₃ = {e₁, e₂, e₃}.

Продолжая указанный процесс, мы через конечное число шагов получим эйлеров цикл μ = {e₁, e₂, …, e_n}, где n — число ребер графа G(X, E).

 

Обоснование алгоритма.

Предположим, что уже построена простая цепь μ_k-1 = {e₁, e₂, …, e_k-1} для k≥2 методом, указанным в алгоритме. Пусть e_k-1 = (x_k-2, x_k-1) и x_k-1 ≠ a. Рассмотрим подграф  , который получается из подграфа G_k-1(X, E\μ_k-1) удалением всех изолированных вершин. Вершина x_k-1 в этом подграфе   имеет нечетную степень, поэтому существует по крайней мере одно ребро e_k∈E\μ_k-1, инцидентное x_k-1. Если это ребро единственное, то оно не является мостом в графе  . В противном случае вершина a будет связана с некоторой вершиной   единственной цепью, содержащей ребро e_k, что противоречит существованию эйлерова цикла в графе G. Поскольку e_k - не мост, то процесс можно продолжать, взяв  . Если ребро e_k не единственное инцидентное вершине x_k-1, то среди этих ребер есть по крайней мере одно, не являющееся мостом. В противном случае один из этих мостов   можно выбросить так, что вершины x_k-1 и a попадут в разные компоненты связности графа  . Если x_k-1 принадлежит компоненте M, то в этой компоненте все вершины имеют четную степень, поэтому существует эйлеров цикл в M, проходящий через x_k-1. Этот цикл содержит все ребра, инцидентные x_k-1 и принадлежащие  , являющиеся одновременно мостами. Получено противоречие, так как ребра из эйлерова цикла мостами быть не могут. Итак, в рассмотренном случае существует ребро e_k, инцидентное вершине x_k-1 и не являющееся мостом. Значит, и в этом случае процесс можно продолжать, взяв

.

Из предыдущего следует, что процесс нельзя продолжать тогда и только тогда, когда мы попадем в вершину a, причем степень вершины a относительно непройденных ребер равна нулю. Докажем, что в этом случае построенный цикл μ - простой цикл. Покажем, что μ содержит все ребра графа G. Если не все ребра графа G принадлежат μ, то не принадлежащие μ ребра порождают компоненты связности C₁, …, C_m (m≥1) в подграфе  . Пусть компонента C_i, 1≤i≤m соединяется с циклом μ в вершине y_i. Если существует ребро e∈μ, такое, что e=(y_i, a), то при построении цикла μ было нарушено правило выбора ребра e, что невозможно. Если часть цикла μ, соединяющая y_i и a, состоит более чем из одного ребра, то первое ребро этой части   было мостом, и поэтому было нарушено правило выбора  , что невозможно. Итак, непройденных ребер быть не может, поэтому μ - эйлеров цикл.