2.1.2. Принцип действия многолучевой дисс

Так как вектор скорости летательного аппарата опре­деляется в общем случае проекциями на три некомпланарных (т.е. лежащих не в одной плоскости) направления, то для определения всех трех составляющих необходимо излучать и принимать сигна­лы минимум по трем лучам антенны. Наибольшее применение нашли трех-четырехлучевые системы с , – расположением лучей (см. рис. 2.4). Эти системы свободны от основных недостатков однолучевых систем.

Рассмотрим подробнее принцип действия трехлучевой системы. Значение доплеровского сдвига частоты определяется равенством (см. рис. 2.4)

, (2.4)

где W_S - проекция полной скорости летательного аппарата на направление излучения; λ₀ – длина волны излучаемого передатчиком сигнала. Задача измерения полной скорости сводится к вычислению трех ее составляющих W_x, W_y, W_z, полученных по трем лучам антенной системы РЛС 1, 2, 3 (см. рис. 2.4).

В системе координат x, y, z направление излучения S определяется углами γ₀ и δ₀ (рис. 2.4), где γ₀ – угол между направлением продольной оси самолета 0x и направлением излучения S, δ₀ – угол между обратным направлением вертикальной оси самолета 0y и проекцией S_yz направления излучения S на плоскость y0z. Вектор полной скорости можно разложить в самолетной системе координат на три составляющие: W_x, W_y, W_z. Проектируя эти составляющие полной скорости на направление излучения S и суммируя их, получаем

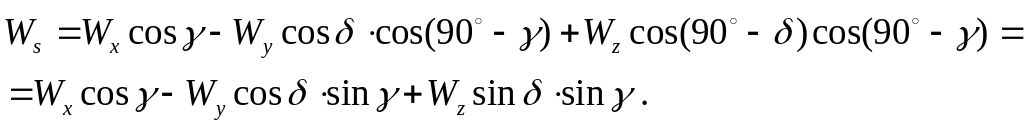(2.5)

Подставляя (2.5) в (2.4), получим

(2.6)

Уравнение (2.6) содержит три независимых неизвестных (W_x, W_y, W_z) и значение полной скорости может быть полностью определено по трем независимым уравнениям типа (2.6), полученным по трем некомпланарным лучам антенной системы.

Расположение лучей антенной системы (типа ), как показано на рис. 2.4. Учитывая, что углы визирования лучей антенны равны соответственно δ₀ и γ₀ (здесь угол δ₀ считается положитель­ным). Подставив значение этих углов для каждого из лучей в уравнение (2.6) и заменив δ на δ₀ при условии γ = γ₀, по­лучим систему уравнений для абсолютных значений доплеровских частот по каждому из лучей антенны:

Рис. 2.4. Расположение лучей в и системах

; (2.7)

; (2.8)

. (2.9)

Используя выражения (2.7), (2.8), (2.9) определяем частоты f_x, f_y, f_z, соответствующие продольной составляющей W_x, верти­кальной составляющей W_y и поперечной составляющей W_z полной скорости ЛА:

; (2.10)

; (2.11)

; (2.12)

откуда получаем соотношения для компонент скорости:

; (2.13)

; (2.14)

; (2.15)

Из геометрии задачи следует, что горизонтальная составляю­щая и угол сноса связаны уравнениями

; (2.16)

; (2.17)

Итак, на первом этапе необходимо измерить величины доплеровских частот и решить уравнения (2.13)-(2.15).