1.3. Задане збурення

Відмова центрального двигуна

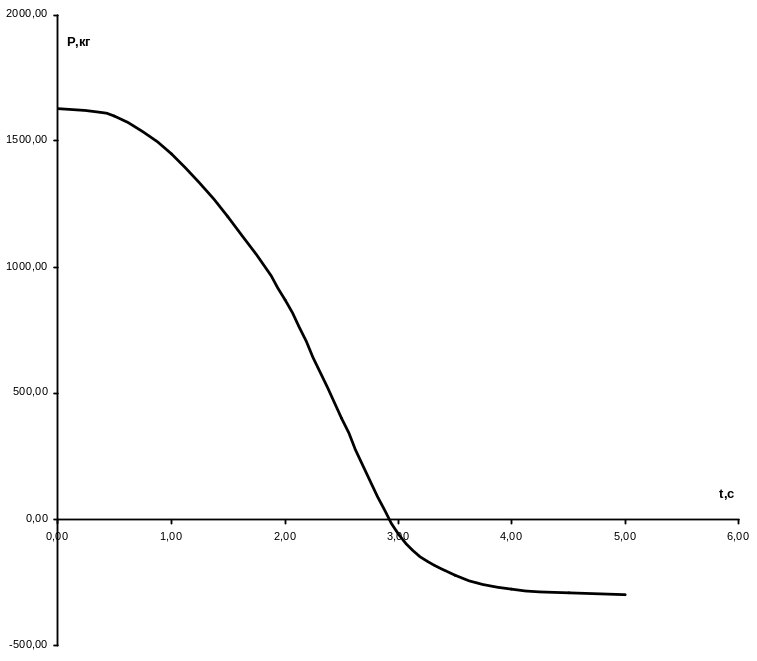
рис.1 Падіння тяги при відмові одного двигуна НК-8-2У

При відмові центрального двигуна сила тяги двох лівого і правого двигунів має збільшитись і пропорційно перерозподілитись між ними з метою стабілізації параметрів польоту при відмові центрального двигуна. Оскільки центральний двигун розміщений трохи вище, ніж повздовжня вісь ПС, то виникає незначний додатковий повздовжній момент, через плече сили від повздовжньої осі літака до осі центрального двигуна. Зважаючи на те, що плече сили мале, нехтуємо моментом, що виникає.

Таким чином, загальна тяга Р_all= 2*Р+ Р1,

Де Р-тяга лівого або правого двигуна ПС,

Р1- сила, прикладена на подолання лобового опору центрального двигуна, що відмовив.

2. Закон автоматичного управління

В даному варіанті реалізується режим стабілізації заданої приладової швидкості:

де

м

3. Методи чисельного інтегрування.

Методи чисельного інтегрування використовуються для розв’язку звичайних диференціальних рівнянь (ЗДР) у випадку, коли для останніх не можливо побудувати аналітичний розв’язок через відомі функції. До того ж, для деяких задач використання методів чисельного інтегрування є більш ефективним, навіть при існування аналітичних розв’язків. Необхідно відмітити деякі особливості цих методів. По-перше, одна задача може бути розв’язана декількома методами. По-друге, сучасні наукові задачі та швидкий розвиток обчислювальної техніки призводять до створення нових методів.

3.1 Метод Ейлера

Найбільш простим методом чисельного інтегрування диференціальних рівнянь є метод Ейлера. Рекурентне співвідношення для інтегрування цим методом має наступний вигляд:

,

де У_i+1, У_i - значення функції на (i+1)-ому та i-ому кроці інтегрування,

У_i - значення першої похідної на i-м кроці,

∆t – крок інтегрування.

З приведеного рекурентного співвідношення випливає, що метод Ейлера дозволяє інтегрувати лише диференціальні рівняння першого порядку. Для інтегрування рівнянь більших порядків їх необхідно звести до системи диференціальних рівнянь, записаних у формі Коші.

3.2. Метод Рунге-Кутти Мерсона

Мерсон запропонував модифікацію метода Рунге-Кутти 4-го порядку, що дозволяє оцінювати похибку на кожному кроці та приймати рішення про зміну кроку. Схему Мерсона за допомогою еквівалентних перетворень приведемо до вигляду, зручному для програмування

, де

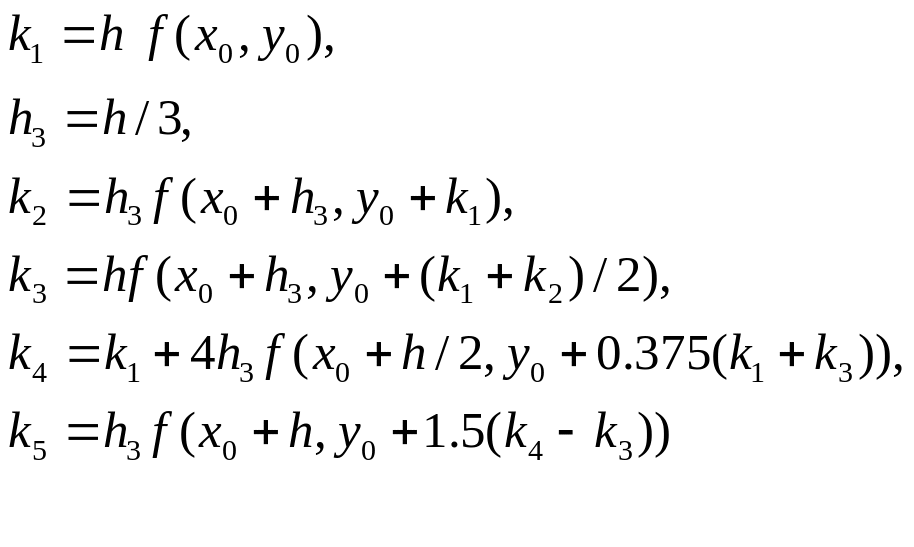
(1)

Схема Мерсона потребує на кожному етапі обчислювати праву частину ДР в п’яти точках, але за рахунок тільки одного додаткового коефіцієнта к_і порівняно з класичною схемою Рунге-Кутта на кожному кроці можна визначити похибку обчислення R за формулою

(2)

Для автоматичного вибору кроку інтегрування рекомендується наступний критерій. Якщо абсолютне значення величини R, обчислене за формулою (2), виявиться більшим за допустиму задану похибку ε,

, то крок h зменшиться в два рази і обчислення за схемою (1) повторяться з точки (x₀, y₀). При виконанні умови

крок h можна подвоїти.

Автоматичний вибір кроку дозволяє значно скоротити час рішення ДР.

При автоматичному виборі кроку інтегрування інколи виникає необхідність вивода результатів тільки у фіксованих точках. Ця можливість також реалізована в програмі.