1.2. Классификация игр

По этим и другим признакам огромное разнообразие игр можно классифицировать. Например, по характеру доступных стратегий игры разделяют: — на конечные или бесконечные (в частности, бесконечные во времени), — на дискретные или непрерывные, — на “статические” (с одновременными ходами), или динамические. По соотношению целей участников игры разделяют на антагонистические или неантагонистические (с непротивоположными интересами). По типу поведения — на кооперативные (где участники ищут компромисс в переговорах), и некооперативные (где договоры неосуществимы или невыполнимы). По информационной структуре игры можно делить на игры с совершенной или несовершенной рациональностью, с общим или необщим знанием данных, и др.. А также, учитывая внешний контекст игры, на 1) уникальные, 2) популяционные (где игроки пользуются знанием о происходивших ранее аналогичных играх), 3) повторяющиеся в том же коллективе (где игроки пользуются угрозами).

Для анализа условия игры обычно формализуют в одной из трех форм: в характеристической (описываются значения выигрышей каждой коалиции, только для кооперативных игр), в развернутой (описываются последовательности возможных ходов), или в стратегической (описываются цельные стратегии). По свойствам функций выигрышей: непрерывные, выпуклые, сепарабельные и т. д. Если сумма выигрышей всех игроков в каждой партии равна нулю, то это — игра с нулевой суммой. Игра двух игроков c нулевой суммой называется антагонистической. В такой игре один игрок выигрывает за счет другого. Конечная антагонистическая игра называется матричной игрой. Сначала мы рассмотрим более простую – нормальную форму, потом развернутую, затем сопоставим их.

Главная задача теории игр состоит в том, чтобы определить оптимальную стратегию для каждого игрока. Оптимальная стратегия для игрока — это такая стратегия, которая максимизирует его ожидаемый выигрыш.

Игры в нормальной форме. Игра в нормальной (или стратигической) форме состоит из спецификации трех вещей:

1. Списка игроков,

2. Для каждого игрока задается список стратегий.

3. Для каждого профиля стратегий указываается профиль платежей (выигрышей) игроков.

Важным предположением, которое играет ключевую роль в теории, состоит в предположении, что все игроки рациональны, в том смысле, что каждый игрок рассматривает имеющиеся в его распоряжении альтернативы, формирует представления относительно неизвестных параметров, имеет четко определенные предпочтения и выбирает свои действия в результате некоторого процесса оптимизации (максимизации своей целевой функции). Более того, не менее существенным является факт общеизвестности (общего знания) рациональности игроков, т. е. все игроки не только рациональны, но и знают, что другие игроки рациональны, что все игроки знают, что все игроки знают, что они рациональны и т. д.

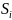Поясним смысл этих данных. Обозначим множество игрроков через N. Типичный игрок обозначается с символом i. Далее, для каждого I ϵ N задается множество стратегий ; типичная стратегия - 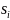Профиль стратегий это набор по стратегии для каждого игрока т.е.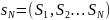 это элемент декартова произведения множеств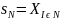 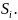Наконец для каждого игрока указывается функция его выигрыша 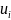: 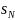R

Неформально каждый игрок выбирает некоторую стратегию когда это сделают все становится ясен его выигрыш. Каждый игрок стремится получить выигрыш побольше. Основная трудность в том, что этот выигрыш зависит не только от его действий, но и от действий остальных игроков. И каждый игрок должен учитывать это в своем поведении. Можно сказать и так: в игре в нормальной форме игроки стратегически независимы, они могут выбирать любые стратегии, но остаются связанными через полезности.

Развернутая форма игры. При таком задании игры больше внимания уделяется порядку ходов и той информации, которая при этом открывается игроку. Начнем с простейших, т.н. позиционных игр, или игр с полной инфор­мацией. Главное здесь - дерево игры; это направленный граф без циклов с выделенной вершиной - корнем. Стрелки идут в направлении от корня. Вер­шины дерева изображают позиции игры, места, где какие-то игроки должны выбрать ход - одну из стрелок, выходящую из этой вершины. Поэтому у каж­дой (нетерминальной) вершины стоит метка того игрока, который делает ход (говорят еще - контролирует эту вершину). В терминальных вершинах (где игра заканчивается) стоит вектор (профиль) выигрышей игроков.

Бескоалиционные и коалиционные игры .

Экономические игры, в которые играют фирмы, могут быть или коалиционными, или бескоалиционными. В коалиционной игре (cooperative game) игроки могут заключать обязывающие контракты (договоры), которые позволяют им планировать совместные стратегии. В бескоалиционной игре (noncooperative game) переговоры и приведение в исполнение обязывающих контрактов (договоров) являются невозможными.

Примером коалиционной игры являются переговоры между покупателем и продавцом о цене ковра. Если издержки производства ковра составляют $100, и покупатель оценивает ковер в $200, для этой игры возможно коалиционное (совместное) решение: соглашение продать ковер по любой цене между $101 и $199 будет максимизировать сумму потребительского излишка покупателя и прибыль продавца, одновременно изменяя положение обеих сторон сделки в лучшую сторону. Другая коалиционная игра могла бы включать две фирмы, ведущие переговоры о совместных инвестициях в разработку новой технологии (предполагается, что ни одна фирма не имеет достаточного ноу-хау, чтобы преуспеть самостоятельно). Если фирмы могут подписать обязывающий стороны договор, чтобы разделить прибыль от их совместной инвестиции, возможен коалиционный исход, ко­торый приводит к улучшению положения обеих фирм.

Примером бескоалиционной игры является ситуация, в которой две соперничающие фирмы учитывают возможное поведение друг друга, когда независимо друг от друга устанавливают свои цены. Каждая фирма знает, что, сбивая цены своего конкурента, она захватит более крупную долю рынка, но, поступая так, она несет риск развязывания ценовой войны. Другой бескоалиционной игрой является аукцион, упомянутый выше: каждый участник торгов должен учитывать возможное поведение других участников, когда определяет оптимальную стратегию предложения цены. Заметим, что фундаментальное различие между коалиционной и бескоалиционной игрой лежит в возможностях заключения договоров. В коалиционных играх возможны обязывающие договоры; в бескоалиционных играх их нет. В основном мы будем иметь дело с бескоалиционными играми. В любой игре, однако, наиболее важным аспектом принятия стратегического решения является понимание точки зрения вашего оппонента и (предполагая, что ваш оппонент является рациональным) выводы о его возможной реакции на ваши действия. Это может показаться очевидным — конечно, необходимо понимать точку зрения оппонента. Но даже в простых игровых ситуациях люди часто игнорируют или неправильно понимают позицию оппонентов и рациональные ответы, которые предполагает их позиция.

Симметричные и несимметричные

	А	Б
А	1, 2	0, 0
Б	0, 0	1, 2
Несимметричная игра

Игра будет симметричной тогда, когда соответствующие стратегии у игроков будут равны, то есть иметь одинаковые платежи. Иначе говоря, если игроки могут поменяться местами и при этом их выигрыши за одни и те же ходы не изменятся. Многие изучаемые игры для двух игроков — симметричные. В частности, таковыми являются: «Дилемма заключённого», «Охота на оленя», «Ястребы и голуби». В качестве несимметричных игр можно привести «Ультиматум» или «Диктатор».

В примере справа игра на первый взгляд может показаться симметричной из-за похожих стратегий, но это не так — ведь выигрыш второго игрока при профилях стратегий (А, А) и (Б, Б) будет больше, чем у первого.

С нулевой суммой и с ненулевой суммой.

Игры с нулевой суммой — особая

	А	Б
А	−1, 1	3, −3
Б	0, 0	−2, 2
Игра с нулевой суммой

разновидность игр с постоянной суммой, то есть таких, где игроки не могут увеличить или уменьшить имеющиеся ресурсы, или фонд игры. В этом случае сумма всех выигрышей равна сумме всех проигрышей при любом ходе. Посмотрите направо — числа означают платежи игрокам — и их сумма в каждой клетке равна нулю. Примерами таких игр может служить покер, где один выигрывает все ставки других; реверси, где захватываются фишки противника; либо банальное воровство. Многие изучаемые математиками игры, в том числе уже упоминавшаяся «Дилемма заключённого», иного рода: в играх с ненулевой суммой выигрыш какого-то игрока не обязательно означает проигрыш другого, и наоборот. Исход такой игры может быть меньше или больше нуля. Такие игры могут быть преобразованы к нулевой сумме — это делается введением фиктивного игрока, который «присваивает себе» излишек или восполняет недостаток средств.

Ещё игрой с отличной от нуля суммой является торговля, где каждый участник извлекает выгоду. Широко известным примером, где она уменьшается, является война.

Параллельные и последовательные. В параллельных играх игроки ходят одновременно, или, по крайней мере, они не осведомлены о выборе других до тех пор, пока все не сделают свой ход. В последовательных, или динамических, играх участники могут делать ходы в заранее установленном либо случайном порядке, но при этом они получают некоторую информацию о предшествующих действиях других. Эта информация может быть даже не совсем полной, например, игрок может узнать, что его противник из десяти своих стратегий точно не выбрал пятую, ничего не узнав о других.

Различия в представлении параллельных и последовательных игр рассматривались выше. Первые обычно представляют в нормальной форме, а вторые — в экстенсивной.

С полной или неполной информацией игры с полной информацией. В такой игре участники знают все ходы, сделанные до текущего момента, равно как и возможные стратегии противников, что позволяет им в некоторой степени предсказать последующее развитие игры. Полная информация не доступна в параллельных играх, так как в них неизвестны текущие ходы противников. Большинство изучаемых в математике игр — с неполной информацией. Например, вся «соль» Дилеммы заключённого или Сравнения монеток заключается в их неполноте.

В то же время есть интересные примеры игр с полной информацией: «Ультиматум», «Многоножка». Сюда же относятся шахматы, шашки, го, манкала и другие.

Часто понятие полной информации путают с похожим — совершенной информации. Для последнего достаточно лишь знание всех доступных противникам стратегий, знание всех их ходов необязательно.

Игры с бесконечным числом шагов. Игры в реальном мире или изучаемые в экономике игры, как правило, длятся конечное число ходов. Математика не так ограничена, и в частности, в теории множестврассматриваются игры, способные продолжаться бесконечно долго. Причём победитель и его выигрыш не определены до окончания всех ходов.

Задача, которая обычно ставится в этом случае, состоит не в поиске оптимального решения, а в поиске хотя бы выигрышной стратегии. Используя аксиому выбора, можно доказать, что иногда даже для игр с полной информацией и двумя исходами — «выиграл» или «проиграл» — ни один из игроков не имеет такой стратегии. Существование выигрышных стратегий для некоторых особенным образом сконструированных игр имеет важную роль в дескриптивной теории множеств.

Дискретные и непрерывные игры. Большинство изучаемых игр дискретны: в них конечное число игроков, ходов, событий, исходов и т. п. Однако эти составляющие могут быть расширены на множество вещественных чисел. Игры, включающие такие элементы, часто называются дифференциальными. Они связаны с какой-то вещественной шкалой (обычно — шкалой времени), хотя происходящие в них события могут быть дискретными по природе. Дифференциальные игры также рассматриваются в теории оптимизации, находят своё применение в технике и технологиях, физике.

Метаигры. Это игры, результатом которых является набор правил для другой игры (называемой целевой или игрой-объектом). Цель метаигр — увеличить полезность выдаваемого набора правил. Теория метаигр связана с теорией оптимальных механизмов (англ.).