19Признак равномерной сходимости Вейерштрасса

Сначала понятие мажорантного ряда, с которым мы на самом деле уже сталкивались, используя признак сравнения. И понятие как раз удобнее объяснить на числовых рядах: говорят, что ряд   мажорирует ряд  , если для любого значения   выполнено неравенство  .

Пример в стиле «меняю рубль на два»:  ряд   мажорирует ряд  . Как самый настоящий мажор: 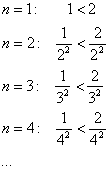Таким образом, для всех   выполнено неравенство  , а значит, ряд   является мажорантным по отношению к ряду  .

Очень, кстати, хорошо, если вы «набили руку» на упомянутом признаке сравнения, а также прорешали соответствующие ряды повышенной сложности – сейчас будет нечто похожее.

Возвращаемся к функциональному ряду   и признаку Вейерштрасса:

Если существует сходящийся числовой ряд  , такой, что для всех   и ДЛЯ ВСЕХ   из некоторого промежутка выполнено неравенство  , то функциональный ряд   в данном промежутке сходится, причём равномерно и абсолютно.

Иными словами, если для функционального ряда   на исследуемом промежутке удастся подобрать мажорирующий его числовой ряд  , то будет нам счастье.

И, как легко видеть, признак Вейерштрасса пригоден не только для доказательства ИМЕННО равномерности, но и для установления самого факта сходимости! С чего мы и начнём.

Пережили сессию – порвали три баяна:

Пример 1

Найти область сходимости функционального ряда 

…как решать? Ведь ряд ни в одном глазу не степенной…. Добавим знаний!

Решение: такой мотив нам тоже встречался – ограниченность синуса. ДЛЯ ЛЮБОГО действительного   и для всех   выполнены неравенства  , поэтому:

Внимание! Если среди членов функционального ряда есть отрицательные, то знак модуля обязателен!

Таким образом, положительный сходящийся ряд   мажорирует функциональный ряд   на всей числовой прямой, а значит, по признаку Вейерштрасса последний сходится равномерно при любом  .

Ответ: область сходимости ряда 

20Определение

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:

Часто рассматривается также ряд, расположенный по степеням (x − x₀), то есть ряд вида

где x₀ − действительное число.

Интервал и радиус сходимости

Рассмотрим функцию 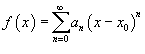 . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.  Если интервал сходимости представляется в виде  , где R > 0, то величина R называетсярадиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.  Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле

или на основе признака Даламбера:

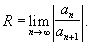
КОШИ - АДАМАРА ТЕОРЕМА

пусть задан степенной ряд 

Если   то ряд (1) сходится только в точке z=a; если   то ряд (1) абсолютно сходится в круге   радиуса 

и расходится вне этого круга при   если   то ряд (1) абсолютно сходится при всех   Содержание К. - А. т. выражается, таким образом, формулой Коши - Адамара (2), к-рую при этом следует понимать в расширенном смысле, включая равенства   Иначе говоря, содержание К.- А. т. состоит в том, что внутренность множества точек (абсолютной) сходимости ряда (1) есть круг   радиуса (2). В случае действительного степенного ряда (1) формула (2) определяет радиус интервала сходимости   В основном К.- А. т. была высказана О. Коши (A. Cauchy) в его лекциях [1], опубликованных в 1821, полную ясность в формулировку и доказательство внес Ж. Адамар [2]. Для степенных рядов 

но n комплексным переменным   обобщением формулы Коши - Адамара является следующее соотношение:

к-рому удовлетворяют сопряженные радиусы сходимости r₁ . . . , r_n ряда (3) (см. Круг сходимости). Записав соотношение (4) в виде   получают уравнение, определяющее границу нек-рой логарифмически выпуклой кратно круговой области с центром а, к-рая и является внутренностью множества точек абсолютной сходимости ряда (3) при n>1.