
- •30. Нормальное уравнение прямой. Расстояние от точки до прямой.
- •31. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
- •32. Взаимное расположение прямых. Нахождение общих точек.
- •33. Окружность. Уравнение окружности.
- •34.Эллипс ( вершины, оси, полуоси, фокусы…).Уравнение эллипса.
- •35.Гипербола (вершина, оси, полуоси, фокусы…). Уравнение гиперболы.
- •36. Парабола. Уравнение параболы.
- •37. Метод координат в пространстве. Основные задачи.
- •38. Различные виды уравнения плоскости.
- •39. Общее уравнение плоскости. Частные случаи.
- •40. Уравнение плоскости, проходящей через три точки.
- •41. Нормальное уравнение плоскости. Расстояние от точки до плоскости.
- •42. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей. Угол между двумя плоскостями
- •Условие параллельности и перпендикулярности двух плоскостей
- •43. Уравнения прямой в пространстве.
- •44. Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности.
39. Общее уравнение плоскости. Частные случаи.
Рассмотрим общее уравнение первой степени с тремя переменными x, y и z:
 .
(12.4)
.
(12.4)
Полагая, что по крайней мере один из
коэффициентов А, В или С не
равен нулю, например
 ,
перепишем уравнение (12.4) в виде
,
перепишем уравнение (12.4) в виде
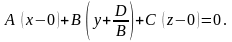 (12.5)
(12.5)
Сравнивая уравнение (12.5) с уравнением
(12.3), видим, что уравнения (12.4) и (12.5)
являются уравнениями плоскости с
нормальным вектором
,
проходящей через точку
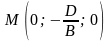 .
.
Итак, уравнение (12.4) определяет в системе координат некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.
Частные случаи общего уравнения плоскости:
Если
 ,
то оно принимает вид
,
то оно принимает вид
 .
Этому уравнению удовлетворяет точка
.
Этому уравнению удовлетворяет точка
 .
Следовательно, в этом случае плоскость
проходит через начало координат.
.
Следовательно, в этом случае плоскость
проходит через начало координат.Если
 ,
то имеем уравнение
,
то имеем уравнение
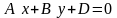 .
Нормальный вектор
.
Нормальный вектор
 перпендикулярен оси
перпендикулярен оси
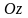 .
Следовательно, плоскость параллельна
оси
;
если В = 0 – параллельна оси Оу,
А = 0 – параллельна оси Ох.
.
Следовательно, плоскость параллельна
оси
;
если В = 0 – параллельна оси Оу,
А = 0 – параллельна оси Ох.Если С = D = 0, то плоскость проходит через параллельно оси Oz. Аналогично, уравнениям
 и
и
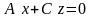 отвечают плоскости, проходящие
соответственно через оси Охи Оу.
отвечают плоскости, проходящие
соответственно через оси Охи Оу.Если А = В = 0, то уравнение (12.4) принимает вид
 ,
т.е.
,
т.е.
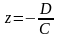 .
Плоскость параллельна плоскости Оху.
Аналогично уравнениям
.
Плоскость параллельна плоскости Оху.
Аналогично уравнениям
 и
и
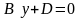 отвечают плоскости, соответственно
параллельные плскостям Оyz
и Oxz.
отвечают плоскости, соответственно
параллельные плскостям Оyz
и Oxz.Если
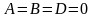 ,
то уравнение (12.4) примет вид
,
то уравнение (12.4) примет вид
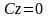 ,
т.е.
,
т.е.
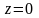 .
Это уравнение плоскости Оху.
Аналогично:
– уравнение плоскости Oxz;
– уравнение плоскости Оyz.
.
Это уравнение плоскости Оху.
Аналогично:
– уравнение плоскости Oxz;
– уравнение плоскости Оyz.
40. Уравнение плоскости, проходящей через три точки.
Три точки пространства, не лежащие на
одной прямой, определяют единственную
плоскость. Найдем уравнение плоскости
Q, проходящей через
три данные точки
 ,
,
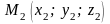 и
и
 ,
не лежащие на одной прямой.
,
не лежащие на одной прямой.
Возьмем на плоскости произвольную
точку
и составим векторы
 ,
,
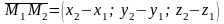 ,
,
 .
Эти векторы лежат на плоскости Q
,следовательно, они компланарны.
Используем условие компланарности
векторов (их смешанное произведение
равно нулю), получаем
.
Эти векторы лежат на плоскости Q
,следовательно, они компланарны.
Используем условие компланарности
векторов (их смешанное произведение
равно нулю), получаем
 ,
т.е.
,
т.е.

(12.6)
Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.
41. Нормальное уравнение плоскости. Расстояние от точки до плоскости.
Нормальным уравнением плоскости называется ее уравнение, написанное в виде
![]() ,
(1)
,
(1)
где ![]() ,
, ![]() ,
, ![]() -
направляющие косинусы нормали
плоскоти, p -
расстояние от начала координат до
плоскости. При вычислении направляющих
косинусов нормали следует считать, что
она направлена от начала координат к
плоскости (если же плоскость проходит
через начало координат, то выбор
положительного направления нормали
безразличен).
-
направляющие косинусы нормали
плоскоти, p -
расстояние от начала координат до
плоскости. При вычислении направляющих
косинусов нормали следует считать, что
она направлена от начала координат к
плоскости (если же плоскость проходит
через начало координат, то выбор
положительного направления нормали
безразличен).
Пусть ![]() -
какая угодно точка пространства, d -
расстояние от нее до данной плоскости.
Отклонением
-
какая угодно точка пространства, d -
расстояние от нее до данной плоскости.
Отклонением ![]() точки
от
данной плоскости называется число +d,
если точка
и
начало координат лежат по разные стороны
от данной плоскости, и число -d, если они
лежат по одну сторону от данной плоскости
(если
лежит
на самой плоскости, то отклонение равно
нулю).
точки
от
данной плоскости называется число +d,
если точка
и
начало координат лежат по разные стороны
от данной плоскости, и число -d, если они
лежат по одну сторону от данной плоскости
(если
лежит
на самой плоскости, то отклонение равно
нулю).
Если
точка
имеет
координаты ![]() ,
, ![]() ,
, ![]() ,
а плоскость задана нормальным уравнением
,
а плоскость задана нормальным уравнением
,
то отклонение точки от этой плоскости дается формулой
![]() .
.
Очевидно, ![]() .
.
Общее уравнение плоскости
![]()
приводится к нормальному виду (1) умножением на нормирущий множитель, определяемый формулой
![]() ;
;
знак нормирующего множителя берется противоположным знаку свободного члена нормируемого уравнения.
