
- •30. Нормальное уравнение прямой. Расстояние от точки до прямой.
- •31. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
- •32. Взаимное расположение прямых. Нахождение общих точек.
- •33. Окружность. Уравнение окружности.
- •34.Эллипс ( вершины, оси, полуоси, фокусы…).Уравнение эллипса.
- •35.Гипербола (вершина, оси, полуоси, фокусы…). Уравнение гиперболы.
- •36. Парабола. Уравнение параболы.
- •37. Метод координат в пространстве. Основные задачи.
- •38. Различные виды уравнения плоскости.
- •39. Общее уравнение плоскости. Частные случаи.
- •40. Уравнение плоскости, проходящей через три точки.
- •41. Нормальное уравнение плоскости. Расстояние от точки до плоскости.
- •42. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей. Угол между двумя плоскостями
- •Условие параллельности и перпендикулярности двух плоскостей
- •43. Уравнения прямой в пространстве.
- •44. Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности.
30. Нормальное уравнение прямой. Расстояние от точки до прямой.
Нормальное уравнение прямой
Пусть прямая определяется заданием p и α (см. рис. 45). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взяв О за полюс и Ох за полярную ось. Уравнение прямой можно записать в виде
 т.е.
т.е. 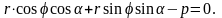
Н

 Следовательно, уравнение (10.10) прямой в
прямоугольной системе координат примет
вид
Следовательно, уравнение (10.10) прямой в
прямоугольной системе координат примет
вид
(10.11)
У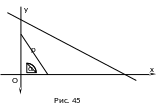 равнение
(10.11) называется нормальным
уравнением прямой.
равнение
(10.11) называется нормальным
уравнением прямой.
Покажем, как привести уравнение (10.4) прямой к виду (10.11).
Умножим все члены
уравнения (10.4) на некоторый множитель
 .
Получим
.
Получим
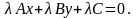 Это уравнение должно обратиться в
(10.11). Следовательно, должны выполняться
равенства:
Это уравнение должно обратиться в
(10.11). Следовательно, должны выполняться
равенства:
 Из первых двух равенств находим
Из первых двух равенств находим
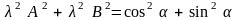 ,т.е.
,т.е.
 Множитель
Множитель
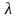 называется нормирующим
множителем.
Согласно третьему равенству
называется нормирующим
множителем.
Согласно третьему равенству
 знак нормирующего множителя противоположен
знаку свободного члена С
общего уравнения прямой.
знак нормирующего множителя противоположен
знаку свободного члена С
общего уравнения прямой.
Пример
10.2. Привести
уравнение
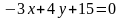 к нормальному виду.
к нормальному виду.
 Решение:
Находим нормирующий множитель
Решение:
Находим нормирующий множитель
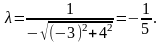 Умножая данное уравнение на
,
получим искомое нормальное уравнение
прямой:
Умножая данное уравнение на
,
получим искомое нормальное уравнение
прямой:

Р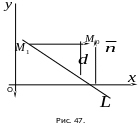 асстояние
от точки до прямой
асстояние
от точки до прямой
Пусть заданы
прямая L
уравнением
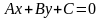 и точка
и точка
 (см. рис. 47). Требуется найти расстояние
от точки
(см. рис. 47). Требуется найти расстояние
от точки
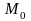 до прямой L.
до прямой L.
Решение: Расстояние
d
от точки
до прямой L
равно модулю проекции вектора
 ,
где
,
где
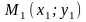 – произвольная точка прямой L,
на направление нормального вектора
– произвольная точка прямой L,
на направление нормального вектора
 .
Следовательно,
.
Следовательно,


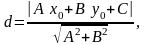
Так как точка
принадлежит прямой L,
то
 ,
т.е.
,
т.е.
 Поэтому
Поэтому
(10.13)
что и требовалось получить.
Пример
10.3. Найти
расстояние от точки
 до прямой
до прямой

Решение: По формуле
(10.13) получаем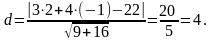
31. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
Пусть прямые
 и
и
 заданы уравнениями с угловыми
коэффициентами
заданы уравнениями с угловыми
коэффициентами
 и
и
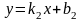 (см. рис. 46).
(см. рис. 46).
Требуется найти угол φ, на который надо повернуть в положительном направлении прямую вокруг точки их пересечения до совпадения с прямой .

Решение: Имеем
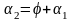 (теорема о внешнем угле треугольника)
или
(теорема о внешнем угле треугольника)
или
 Если
Если
 ,
то
,
то
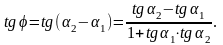
Н

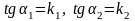 ,
поэтому
,
поэтому
(10.12)
откуда легко получим величину искомого угла.
Если требуется
вычислить острый угол между прямыми,
не учитывая, какая прямая является
первой, какая – второй, то правая часть
формулы (10.12) берется по модулю, т.е.
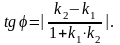
Если прямые
и
параллельны, то
 и
и
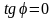 .
Из формулы (10.12) следует
.
Из формулы (10.12) следует
 ,
т.е.
,
т.е.
 .
И обратно, если прямые
и
таковы, что
,
то
,
т.е. прямые параллельны. Следовательно,
условием
параллельности двух прямых является
равенство их угловых коэффициентов:
.
И обратно, если прямые
и
таковы, что
,
то
,
т.е. прямые параллельны. Следовательно,
условием
параллельности двух прямых является
равенство их угловых коэффициентов:
 .
.
Если прямые
и
перпендикулярны, то
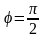 .
Следовательно,
.
Следовательно,
 .
Отсюда
.
Отсюда
 ,
т.е.
,
т.е.
 (или
(или
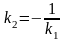 ).
Справедливо и обратное утверждение.
Таким образом, условием
перпендикулярности прямых является
равенство
.
).
Справедливо и обратное утверждение.
Таким образом, условием
перпендикулярности прямых является
равенство
.
