§ 11. Связь между напряженностью электрического поля и потенциалом

В предыдущих параграфах было выяснено, что электрическое поле можно описать либо с помощью векторной величины , либо с помощью скалярной величины . Очевидно, что между этими величинами должна существовать определенная связь. Если учесть, что пропорционально силе, действующей на заряд, а  – потенциальной энергии заряда, легко сообразить, .что эта связь должна быть аналогична, связи между потенциальной энергией и силой. Действительно, работа сил поля над зарядом q на отрезке пути dl может быть представлена, с одной стороны, как qE_ldl, с другой же стороны – как убыль потенциальной энергии заряда, т. е. как

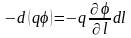
Приравнивая эти выражения, получим

откуда находим, что

(11.1)

где через l обозначено произвольно выбранное направление в пространстве. В частности,

(11.2)

Откуда

Выражение, стоящее в скобках, называется градиентом скаляра  (обозначается grad ). Используя обозначение градиента, можно записать:

(11.3)

Таким образом, напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком. Градиент некоторой скалярной функции (х,у,z) есть векторная величина, обладающая следующими свойствами. Направление градиента совпадает с направлением n, в котором при смещении из данной точки функция , возрастая по величине, изменяется с наибольшей скоростью. Величина производной по этому направлению дает модуль градиента. Частные производные 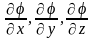представляют собой проекции градиента на координатные оси х, у, z. Аналогично производная 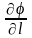, взятая по произвольному направлению l, будет проекцией градиента на это направление. Проекция градиента на перпендикулярное к нему направление , очевидно, равна нулю.

§ 12. Эквипотенциальные поверхности

Для наглядного изображения поля можно вместо линий напряженности воспользоваться поверхностями равного потенциала или эквипотенциальными поверхностями. Как следует из ее названия, эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Если потенциал задан как функция х, у и z, уравнение эквипотенциальной поверхности имеет вид

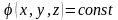
Рисунок 12.1. Эквипотенциальная поверхность и напряженность поля

Направление нормали к эквипотенциальной поверхности будет совпадать с направлением вектора в той же точке. Чтобы убедиться в этом, проведем в некоторой точке касательную  к поверхности (Рисунок 12.1). При смещении вдоль  на бесконечно малую величину d потенциал  не изменится, так что 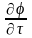равно нулю. Но с точностью до знака равно проекции вектора на направление . Следовательно, тангенциальная составляющая равна нулю, откуда вытекает, что вектор направлен по нормали к поверхности. Учтя, что вектор вместе с тем направлен по касательной к линии , легко сообразить, что линии напряженности в каждой точке ортогональны эквипотенциальным поверхностям.

Эквипотенциальную поверхность можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Уславливаются, однако, проводить поверхности таким образом, чтобы разность потенциалов 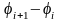для двух соседних поверхностей была, всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля. Действительно, чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности. Следовательно, тем больше в данном месте grad , а значит и .