§ 107. Описание свойств векторных полей

Поток вектора через некоторую поверхность и циркуляция вектора по заданному контуру позволяют судить о характере векторного поля. Однако эти величины дают среднюю характеристику поля в пределах объема, охватываемого поверхностью, через которую определяется поток, или в окрестности контура, по которому берется циркуляция. Уменьшая размеры поверхности или контура (стягивая их в точку), можно прийти к величинам, которые будут характеризовать векторное поле в данной точке. Для того чтобы ввести эти величины, нам придется более глубоко вникнуть в смысл понятий потока и циркуляции.

Пусть нам дано поле вектора скорости несжимаемой неразрывной жидкости. Поток вектора скорости через некоторую поверхность дает, как мы знаем, объем жидкости, протекающей через эту поверхность в единицу времени. Возьмем в окрестности точки Р воображаемую замкнутую поверхность S. Если в объеме V, ограниченном поверхностью, жидкость не возникает и не исчезает, то поток, вытекающий наружу через поверхность, будет, очевидно, равен нулю. Отличие потока от нуля будет указывать на то, что внутри поверхности имеются источники или стоки жидкости, т. е. точки, в которых жидкость поступает в объем (источники), либо удаляется из объема (стоки). Величина потока определяет суммарную алгебраическую мощность источников и стоков. При преобладании источников над стоками величина потока будет положительной, при преобладании стоков – отрицательной.

Частное от деления потока Ф_жидк на величину объема, из которого поток вытекает, т. е.

(107.1)

назовем средней удельной мощностью источников, заключенных в объеме V. Чем меньше объем V, включающий в себя точку Р, тем ближе это среднее к истинной удельной мощности в этой точке. В пределе при стремлении V к нулю, т. е. при стягивании объема V к точке Р, выражение (107.1) даст истинную удельную мощность источников в точке Р, которую называют дивергенцией вектора 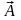. Итак, по определению

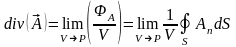(107.2)

Интеграл берется по произвольной замкнутой поверхности S, ограничивающей объем V. Поскольку совершается переход VP, при котором S стремится к нулю, от формы поверхности выражение (107.2) зависеть не может.

Из определения (107.2) следует, что дивергенция есть скалярная функция координат, определяющих положения точек в пространстве. Определение (107.2) является самым общим, не зависящим от выбора координатной системы.

Зная дивергенцию вектора в каждой точке пространства, можно вычислить поток этого вектора через любую поверхность конечных размеров.

Это соотношение носит название теоремы Остроградского – Гаусса.

Циркуляция любого вектора по произвольному контуру Г:

(107.6)

Циркуляция характеризует свойства поля, усредненные по области с размерами порядка поперечника контура Г. Чтобы получить характеристику свойств поля в точке Р, нужно уменьшать размеры контура Г, стягивая его в точку Р. Однако сама циркуляция при этом обратится в нуль. Действительно, среднее значение A_l - конечная величина, а длина контура l в пределе равна нулю. Следовательно, и произведение A_ll обращается в нуль. Поэтому целесообразно в качестве характеристики поля вектора в точке Р взять предел отношения циркуляции вектора по плоскому контуру Г, стягивающемуся к точке Р, к величине площади контура S:

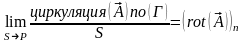(107.7)

Таким образом, величина (107.7) ведет себя как проекция некоторого вектора на направление нормали к плоскости контура, по которому берется циркуляция. Максимальное значение величины (107.7) определяет модуль этого вектора, а направление положительной нормали n, при котором достигается максимум, дает направление вектора. Этот вектор называется ротором вектора .

Под подразумевается проекция вектора на положительную нормаль к площадке S, охватываемой контуром Г.

Выражение (107.7) может служить определением вектора . Из него следует, что ротор есть векторная функция точки Р. Определение (107.8) является самым общим, не зависящим от выбора системы координат.

Таким образом, мы пришли к соотношению

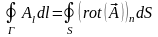(107.14)

которое носит название теоремы Стокса.