§ 3. Системы единиц

С 1 января 1963 г. в нашей стране был введен в действие Государственный стандарт, которым предписывается предпочтительное применение Международной системы единиц, обозначаемой символом СИ. Основными единицами этой системы являются метр, килограмм, секунда, ампер, градус Кельвина. Единицей силы в СИ служит ньютон.

При установлении единиц измерения электрических и магнитных величин СИ исходит не из закона взаимодействия зарядов, а проводников с током. Поэтому коэффициент пропорциональности в формуле закона Кулона оказывается отличной от единицы размерной величиной.

Единицей заряда в СИ является кулон. Чтобы составить представление о величине заряда в 1 Кл, можно вычислить силу, с которой взаимодействовали бы два точечных заряда величиной 1 Кл каждый, находящихся на расстоянии 1 м друг от друга. В соответствии с формулами и результатами измерений

F=910⁹ Н

Это большая величина, и точечные заряды величиной порядка одного кулона в окружающем нас мире встречаются редко. Для справки: заряд электрона равен

-1,6*10^-19 Кл.

§ 4. Рационализованная запись формул

Во многие формулы электродинамики, входят множителями 4 и так называемая электродинамическая постоянная с, равная скорости света в пустоте. Для того, что бы избавиться от них в практически наиболее важных формулах, коэффициент пропорциональности в законе Кулона полагают равным 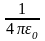. Тогда выражение закона для зарядов, помещающихся в пустоте, принимает вид

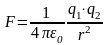(4.1)

Величину ₀ называют электрической постоянной. Она имеет размерность электрической емкости, деленной на длину. Соответственно ее выражают в единицах, называемых Фарад/метр.

Чтобы найти численное значение ₀, подставим в формулу значения величин, соответствующие случаю двух зарядов по 1 Кл, расположенных на расстоянии друг от друга, равном 1 м. Из предыдущего параграфа мы знаем, что сила взаимодействия в этом случае равна 910⁹ Н. Подставив это значение силы, а также 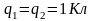в формулу, получим

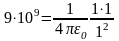
откуда

Ф/м (4.2)

§ 5. Электрическое поле. Напряженность поля

Взаимодействие между зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку электрический заряд оказывается под действием силы. Следовательно, для того чтобы выяснить, имеется ли в данном месте электрическое поле, нужно поместить туда заряженное тело (в дальнейшем для краткости мы будем говорить просто заряд) и установить, испытывает оно действие электрической силы или нет. По величине силы, действующей на данный заряд, можно, очевидно, судить об «интенсивности» поля.

Итак, для обнаружения и исследования электрического поля нужно воспользоваться некоторым «пробным» зарядом. Для того чтобы сила, действующая на пробный заряд, характеризовала поле «в данной точке», пробный заряд должен быть точечным. В противном случае сила, действующая на заряд, будет характеризовать свойства поля, усредненные по объему, занимаемому телом, которое несет на себе пробный заряд.

Исследуем с помощью точечного пробного заряда q_пр поле, создаваемое точечным зарядом q. Поместив пробный заряд в точку, положение которой относительно заряда q определяется радиусом-вектором 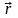, мы обнаружим, что на пробный заряд действует сила

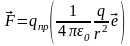(5.1)

Из формулы следует, что сила, действующая на пробный заряд, зависит не только от величин, определяющих поле (от q и r), но и от величины пробного заряда q_пр. Если брать разные по величине пробные заряды, то и силы, которые они испытывают в данной точке поля, будут различны. Легко, однако, видеть, что отношение для всех пробных зарядов будет одно и то же и зависит лишь от величин q и r, определяющих поле в данной точке. Поэтому естественно принять это отношение в качестве величины, характеризующей электрическое поле:

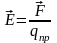(5.2)

Векторную величину 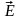называют напряженностью электрического поля в данной точке (т. е. в той точке, в которой пробный заряд испытывает действие силы ).

В соответствии с формулой напряженность электрического поля численно равна силе, действующей на единичный точечный заряд, находящийся в данной точке поля. Направление вектора совпадает с направлением силы, действующей на положительный заряд.

К понятию о напряженности электрического поля мы пришли, исследуя поле точечного заряда. Однако определение распространяется и на случай поля, создаваемого любой совокупностью зарядов. В этом случае, впрочем, необходимо следующее уточнение. Может случиться, что взаимное расположение зарядов, обусловливающих исследуемое поле, изменяется под воздействием, пробного заряда. Это произойдет, например, когда заряды, создающие поле, расположены на проводнике и могут свободно перемещаться в его пределах. Поэтому, чтобы не внести изменений в исследуемое поле, величину пробного заряда нужно брать достаточно малой.

Как следует из формул, напряженность поля точечного заряда пропорциональна величине заряда q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля:

(5.3)

Направлен вектор вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.

За единицу напряженности электрического поля принимается напряженность в такой точке, в которой на заряд, равный единице (1 Кл) действует сила, величина которой также единица (1 Н). В СИ единица напряженности электрического поля имеет название вольт на метр и обозначается В/м.

Согласно формуле заряд в 1 Кл создает в пустоте на расстоянии 1 м напряженность

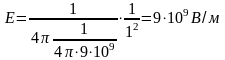
Сила, действующая на пробный заряд, равна

Очевидно, что на всякий точечный заряд q в точке поля с напряженностью будет действовать сила

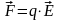(5.4)

Если заряд q положителен, направление силы совпадает с направлением вектора . В случае отрицательного q направления векторов и противоположны.