§ 30. Закон Джоуля – Ленца

При прохождении по проводнику тока проводник нагревается. Джоуль и независимо от него Ленц обнаружили экспериментально, что количество выделяющегося в проводнике тепла пропорционально его сопротивлению, квадрату силы тока и времени:

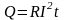(30.1)

Если сила тока изменяется со временем, то

(30.2)

Эти соотношения выражают закон Джоуля – Ленца. Подставляя R в омах, i в амперах, а t в секундах, Q получим в джоулях.

От формулы (30.1), определяющей тепло, выделяемое во всем проводнике, можно перейти к выражению, характеризующему выделение тепла в различных местах проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля — Ленца за время dt в этом объеме выделится тепло

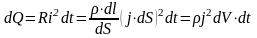(30.3)

где – величина элементарного объема.

Количество тепла dQ, отнесенное к единице времени и единице объема, назовем удельной мощностью тока w.

(30.4)

Воспользовавшись соотношением между j, E,  и , формуле можно придать следующий вид:

(30.5)

Формулы (30.4) и (30.5) выражают закон Джоуля – Ленца в дифференциальной форме. Чтобы, исходя из них, получить количество тепла, выделяющееся во всем проводнике за время t, нужно проинтегрировать w по объему проводника в некоторый момент времени t, а затем полученное выражение проинтегрировать по времени t:

§ 31. Разветвленные цепи. Правила Кирхгофа

Расчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированными Кирхгофом. Этих правил два. Первое из них относится к узлам цепи. Узлом называется точка, в которой сходится более чем два проводника (Рисунок 31).

Рис. 31. Узел из трех проводников

Ток, текущий к узлу, считается имеющим один знак (плюс или минус), текущий от узла — имеющим другой знак (минус или плюс). Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:

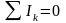(31.1)

Справедливость этого утверждения вытекает из следующих соображений. Если бы алгебраическая сумма токов была отлична от нуля, в узле происходило бы накапливание или уменьшение заряда, что в свою очередь приводило бы к изменению потенциала узла и изменению текущих в цепи токов.

Уравнение (31.1) можно написать для каждого из N узлов цепи. Однако независимыми являются только N-1 уравнение, уравнение N будет следствием из них.

Выделим мысленно в разветвленной цепи произвольный замкнутый контур (смотри контур 1–2–3–4–1 на Рисунок 32).

Рис. 32. Замкнутый контур в электрической цепи

Зададимся направлением обхода (например, по часовой стрелке, как указано на рисунке) и применим к каждому из неразветвленных участков контура закон Ома:

При сложении этих выражений потенциалы сокращаются, и получается уравнение

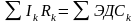(31.2)

которое выражает второе правило Кирхгофа.

Уравнение может быть составлено для всех замкнутых контуров, которые можно выделить мысленно в данной разветвленной цепи. Но независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров друг на друга.

Рис. 33. Расчет электрической цепи по правилам Кирхгофа

Так, например, для цепи, изображенной на Рисунке 33, можно составить три уравнения:

1) для контура 1–2–3–6–1,

2) для контура 3–4–5–6–3,

3) для контура 1–2–3–4–5–6–1.

Последний контур получается наложением первых двух. Следовательно, указанные уравнения не будут независимыми. В качестве независимых можно взять любые два уравнения из трех.

При составлении уравнений второго правила Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода. Например, ток I₁ на Рисунке 33 нужно считать отрицательным, так как он течет навстречу выбранному направлению обхода. ЭДС₁ также нужно приписать знак «-», так как она действует в направлении, противоположном направлению обхода, и т. д.

Направления обхода в каждом из контуров можно выбирать совершенно произвольно и независимо от выбора направлений в других контурах. При этом может случиться, что один и тот же ток либо одна и та же ЭДС войдет в разные уравнения с различными знаками (так получается с током I₂ на Рисунке 33 при указанных направлениях обхода в контурах). Это, однако, не имеет никакого значения, потому что изменение направления обхода вызывает лишь изменение всех знаков в уравнении на обратные.

Составляя уравнения, следует помнить, что через любое сечение неразветвленного участка цепи течет один и тот же ток.

Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы ЭДС и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи. Можно решить и задачи иного рода, например найти ЭДС, которые нужно включить в каждый из участков цепи, чтобы получить при заданных сопротивлениях нужные токи.