16.1.1. Понятие рациональной дроби

 О: Под рациональной дробью понимается функция

 

 

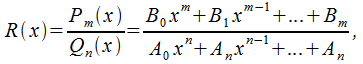
В данном случае - определенные коэффициенты, Рациональная дробь именуется правильной, при условии, что , и неправильной, в случае .

Любую неправильную рациональную дробь можно записать в виде суммы многочлена и привильной дроби.

Допустим, что - это неправильная рациональная дробь. Осуществим деление числителя на знаменатель, в итоге имеем:

 

 

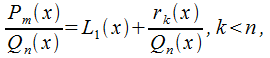
в данном случае и остаток представлены в виде многочленов, а - это правильная рациональная дробь.

 

Пример:

 

 

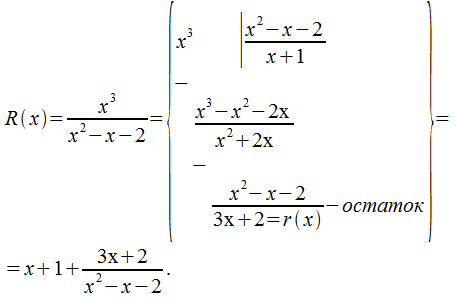
Итак, - остаток.

Первый интеграл найти не трудно. Для определения второго интеграла, следует подынтегральную функцию записать в виде сумы простейших рациональных дробей, далее надо их проинтегрировать. С этой целью разберем простейшие рациональные дроби.

 

16.1.2. Простейшие рациональные дроби и их интегрирование

 1 тип.

  - заданные числа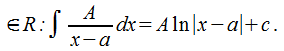

 

2 тип.

- заданные числа

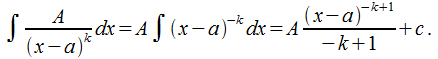
3 тип.

- заданные числа . Квадратный трехчлен не содержит действительных корней.

Интегрирование осуществляется посредством выделения полного квадрата в знаменателе: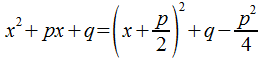 и дальнейшей заменой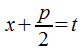 , иначе выражаясь

 

 

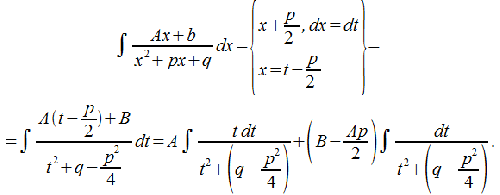
Первый инеграл посредством осуществления замены приводится к табличному (ОК № 15, формула 2), второй — табличный (формула 15).

Пример:

 

 

4 тип.

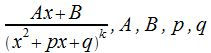- заданные числа не содержит действительных корней.

 

16.1.3. Разложение правильной рациональной дроби на простейшие

 Представим, что знаменатель правильной рациональной дроби не содержит действительных корней.

Тогда можно записать в виде суммы простейших дробей 1-3 типов:

 

 

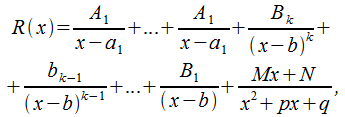
в данном случае представлены в качестве коэффициентов, которые определяются посредством приведения суммы справа к общему знаменателю и дальнейшего приравнивания полученного числителя к .

 

Пример 1:

 

 

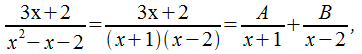
Пример 2:

 

 

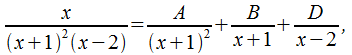
Пример 3:

 

 

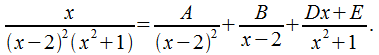
Два метода определения коэффициентов в разложении разберем на примере.

 

Пример:

 

 

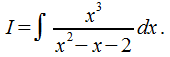
Учитывая то, что , то

 

 

Запишем рациональную дробь под интегралом как сумму простейших:

 

(16.1)

 

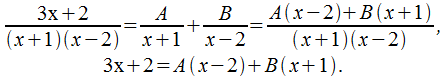
Первый метод именуется методом неопределенных коэффициентов. Его сущность сводится к приравниванию коэффициентов при эквивалентных степенях в (16.1):

 

 

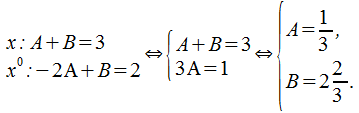
Второй метод известен как метод частных значений. Его сущность сводится к подстановке значений (16.1), сначала корней знаменателя:

 

 

В итоге получаем

 

23 Вопрос. Интегрирование рационально-тригонометрических функций. Примеры

Интегралы от тригонометрических функций. Примеры решений

На данном уроке мы рассмотрим интегралы от тригонометрических функций, то есть начинкой интегралов у нас будут  синусы, косинусы, тангенсы и котангенсы в различных комбинациях. Все примеры будут разобраны подробно, доступно и понятно даже для чайника.

Для успешного изучения интегралов от тригонометрических функций Вы должны хорошо ориентироваться в простейших интегралах, а также владеть некоторыми приемами интегрирования. Ознакомиться с этими материалами можно на лекциях Неопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле.  А сейчас нам потребуются: Таблица интегралов, Таблица производных и Справочник тригонометрических формул. Все методические пособия можно найти на странице Математические формулы и таблицы. Рекомендую всё распечатать. Особо заостряю внимание на тригонометрических формулах, они должны быть перед глазами – без этого эффективность работы заметно снизится.

Но сначала о том, каких интегралов в данной статье нет. Здесь не найдется интегралов вида  ,   – косинус, синус, умноженный на какой-нибудь многочлен (реже что-нибудь с тангенсом или котангенсом). Такие интегралы интегрируются по частям, и для изучения метода посетите урок Интегрирование по частям. Примеры решений.Также здесь не найдется интегралов с  «арками» – арктангенсом, арксинусом и др., они тоже чаще всего интегрируются по частям.

При нахождении интегралов от тригонометрических функций используется ряд методов:

Использование тригонометрических формул

Понижение степени подынтегральной функции (частный случай п.1)

Метод замены переменной

Универсальная тригонометрическая подстановка (частный случай п.3)

В рамках урока я постараюсь подробно разобрать все перечисленные методы и привести примеры решения типовых интегралов. Следует отметить, что данное разделение по параграфам весьма условно, поскольку очень часто вышеперечисленные правила используются одновременно.

Использование тригонометрических формул

Пример 1

Найти неопределенный интеграл.

Сначала полное решение, потом комментарии.

Используем формулу:

(1) Мы видим, что в подынтегральном выражении находится произведение двух функций. К сожалению, в интегральном исчислении нет удобной формулы для интегрирования произведения:  , поэтому приходится прибегать к различным ухищрениям. В данном случае мы прерываем решение значком   и поясняем, что используется тригонометрическая формула. Данная формула превращает произведение в сумму.

(2) Используем свойства линейности неопределенного интеграла – интеграл от суммы равен сумме интегралов; константу можно (и нужно) вынести за знак интеграла.

! Справка: При работе с тригонометрическими функциями следует помнить, что:

Косинус – это четная функция, то есть  , минус исчезает без всяких последствий. В рассматриваемом примере: 

Синус – функция нечетная:   – здесь минус, наоборот – не пропадает, а выносится.

(3) Под интегралами у нас сложные функции (косинусы не просто от  , а от сложного аргумента). Это простейшие из сложных функций, интегралы от них удобнее найти методом подведения под знак дифференциала. Более подробно с данным приёмом можно ознакомиться на уроке Метод замены переменной в неопределенном интеграле. (4) Используем табличную формулу  , единственное отличие, вместо «икса» у нас сложное выражение.

Готово.

 Пример 2

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Пример 3

Найти неопределенный интеграл.

Классика жанра для тех, кто тонет на зачёте. Как Вы, наверное, заметили, в таблице интегралов нет интеграла от тангенса и котангенса, но, тем не менее, такие интегралы найти можно.

(1) Используем тригонометрическую формулу 

(2) Подводим функцию под знак дифференциала.

(3) Используем табличный интеграл  .

Пример 5

Найти неопределенный интеграл.

Степени у нас будут потихоньку повышаться =). Сначала решение:

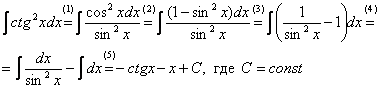
(1) Используем формулу 

(2) Используем основное тригонометрическое тождество  , из которого следует, что  .

(3) Почленно делим числитель на знаменатель.

(4) Используем свойство линейности неопределенного интеграла.

(5) Интегрируем с помощью таблицы.

Понижение степени подынтегральной функции

Данный приём работает, когда подынтегральные функции нафаршированы синусами и косинусами в чётных степенях. Для понижения степени используют тригонометрические формулы  ,   и  , причем последняя формула чаще используется в обратном направлении:  .

Пример 7

Найти неопределенный интеграл.

Решение:

В принципе, ничего нового здесь нет, за исключением того, что мы применили формулу   (понизив степень подынтегральной функции). Обратите внимание, что я сократил решение. По мере накопления опыта интеграл от   можно находить устно, это экономит время и вполне допустимо при чистовом оформлении заданий. В данном случае целесообразно не расписывать и правило  , сначала устно берем интеграл от 1, затем – от  .

Пример 8

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Таки обещанное повышение степени:

Пример 9

Найти неопределенный интеграл.

Сначала решение, потом комментарии:

(1) Готовим подынтегральную функцию для применения формулы  .

(2) Собственно применяем формулу.

(3) Возводим знаменатель в квадрат и выносим константу за знак интеграла. Можно было поступить несколько иначе, но, на мой взгляд, так удобнее.

(4) Используем формулу 

(5) В третьем слагаемом снова понижаем степень, но уже с помощью формулы  .

(6) Приводим подобные слагаемые (здесь я почленно разделил   и выполнил сложение  ).

(7) Собственно берём интеграл, правило линейности   и метод подведения функции под знак дифференциала выполняем устно.

(8) Причесываем ответ.

! В неопределенном интеграле нередко ответ можно записать несколькими способами

В только что рассмотренном примере окончательный ответ   можно было записать иначе – раскрыть скобки и даже это сделать еще до интегрирования выражения, то есть вполне допустима следующая концовка примера:

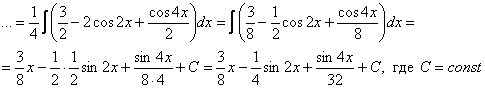
Метод замены переменной

Как уже упоминалось в статье Метод замены переменной в неопределенном интеграле, основной предпосылкой для использования метода замены является тот факт, что в подынтегральном выражении есть некоторая функция   и её производная  :  (функции  ,   не обязательно находятся в произведении)

Пример 11

Найти неопределенный интеграл.

Смотрим в таблицу производных и замечаем формулы  ,  , то есть, в нашем подынтегральном выражении есть функция и её производная. Однако мы видим, что при дифференцировании косинус и синус взаимно превращаются друг в друга, и возникает вопрос: как выполнить замену переменной и что же  обозначать за   – синус или косинус?! Вопрос можно решить методом научного тыка: если мы неправильно выполним замену, то ничего хорошего не получится.

Общий ориентир: в похожих случаях за   нужно обозначить функцию, которая находится в знаменателе.

Прерываем решение и проводим замену

В знаменателе у нас всё хорошо, всё зависит только от  , теперь осталось выяснить, во что превратится  . Для этого находим дифференциал  :

Или, если короче:  Из полученного равенства по правилу пропорции выражаем нужное нам выражение:

Итак: Теперь всё подынтегральное выражение у нас зависит только от   и можно продолжать решение

Готово. Напоминаю, что цель замены – упростить подынтегральное выражение, в данном случае всё свелось к интегрированию степенной функции по таблице.

Я не случайно так подробно расписал этот пример, это сделано в целях повторения и закрепления материалов урока Метод замены переменной в неопределенном интеграле.

 А сейчас два примера для самостоятельного решения:

Пример 12

Найти неопределенный интеграл.

Пример 13

Найти неопределенный интеграл.

Полные решения и ответы в конце урока.

Пример 14

Найти неопределенный интеграл.

Здесь опять в подынтегральном выражении находятся синус с косинусом (функция с производной), но уже в произведении, и возникает дилемма – что же обозначать за  , синус или косинус?

Можно попытаться провести замену методом научного тыка, и, если ничего не получится, то обозначить за   другую функцию, но есть:

Общий ориентир: за   нужно обозначить ту функцию, которая, образно говоря, находится в «неудобном положении».

Мы видим, что в данном примере студент косинус «мучается» от степени, а синус – свободно так сидит, сам по себе. 

Поэтому проведем замену:

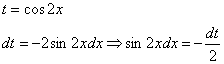
Если у кого остались трудности с алгоритмом замены переменной и нахождением дифференциала  , то следует вернуться к уроку Метод замены переменной в неопределенном интеграле.

Пример 15

Найти неопределенный интеграл.

Анализируем подынтегральную функцию, что нужно обозначить за  ? Вспоминаем наши ориентиры: 1) Функция, скорее всего, находится в знаменателе; 2) Функция находится в «неудобном положении».

Кстати, эти ориентиры справедливы не только для тригонометрических функций.

Под оба критерия (особенно под второй) подходит синус, поэтому напрашивается замена  . В принципе, замену можно уже проводить, но сначала неплохо было бы разобраться, а что делать с  ? Во-первых, «отщипываем» один косинус:

 мы резервируем под наш «будущий» дифференциал 

А   выражаем через синус с помощью основного тригонометрического тождества:

Вот теперь замена: 

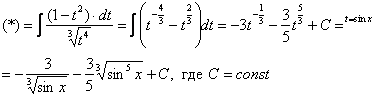
Готово.

Пример 19

Найти неопределенный интеграл.

Здесь перед применением универсальной тригонометрической подстановки необходимо понизить степени в знаменателе при помощи формул  ,  . Попробуйте разобраться в данном примере самостоятельно, полное решение и ответ очень близко!

Пример 19: Решение:

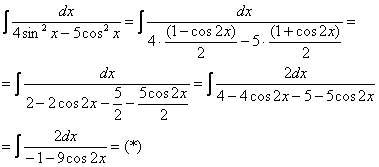
Универсальная тригонометрическая подстановка:

24.Вопрос.Интегрирование простейших иррациональностей. Примеры.

Рассмотрим случаи, в которых замена переменных позволяет интегралы от иррациональных функций свести к интегралам от рациональных функций, то есть рационализировать интеграл.

I. Интегралы вида  рационализируются заменой переменной:

, где k – наименьшее общее кратное чисел m и n.

(20)

Пример 6. Вычислить интеграл  .

Решение: 

.

II. В общем случае интегралы вида  вычисляются заменой переменной:

(21)

Пример 7. Вычислить интеграл  .

Решение:  .

Раскладывая по методу неопределенных коэффициентов подынтегральную функцию получим следующий интеграл:

Поскольку  полученный интеграл можно представить в виде:

.

III. В общем случае интегралы вида  вычисляются заменой переменной:

(22)

Пример 8. Вычислить интеграл  .

Решение: 

Раскладывая по методу неопределенных коэффициентов подынтегральную функцию получаем:

.

Поскольку  , полученный интеграл можно записать в виде:

.

IV. В общем случае интегралы вида  вычисляются заменой переменной:

или

(23)

Пример 9. Вычислить интеграл  .

Решение: 

25.Вопрос.Понятие определённого интеграла. Геометрический и физический смысл определённого интеграла.

Таблица интегралов, таблица неопределенных интегралов

У всех школьников и студентов возникают проблемы с интегралами. У нас на сайт Вы найдете уникальную таблицу интегралов. В нашей таблице интегралов мы постарались собрать самое полное собрание формул, которое поможет Вам решить любой интеграл. Неизменными спутниками таблицы интегралов являются - таблица производных и формулы производных , которые также в полном виде представлена у нас на сайте. Читайте наш сайт и учиться Вам станет на много проще!

Основные формулы

Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где  ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись

Как видно на графиках внизу (приращение первообразной функции обозначено  ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F(b) - F(a)).

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.

Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,

            (38)

Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

                   (39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому

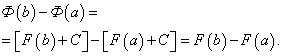
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.

Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее - значение нижнего предела a и вычисляется разностьF(b) - F(a). Полученное число и будет определённым интегралом..

При a = b по определению принимается

Для того чтобы потренироваться в нахождении определённых интегралов, потребуется таблица основных неопределённых интегралов и пособие "Действия со степенями и корнями".

Пример 1. Вычислить определённый интеграл

Решение. Сначала найдём неопределённый интеграл:

Применяя формулу Ньютона-Лейбница к первообразной

(при С = 0), получим

Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).

Проверить решение можно на калькуляторе неопределённых интегралов онлайнВ полученную в результате вычисления первообразную подставьте сначала значение верхнего предела, затем значение нижнего предела и найдите разницу. Полученное число и будет определённым интегралом.

Пример 2. Вычислить определённый интеграл

Решение. Используя формулу

получим

Проверить решение можно на калькуляторе неопределённых интегралов онлайнВ полученную в результате вычисления первообразную подставьте сначала значение верхнего предела, затем значение нижнего предела и найдите разницу. Полученное число и будет определённым интегралом.

Геометрический и физический смысл определенного интеграла