Наибольшее и наименьшее значения функции на отрезке

Миниатюрная и довольно простая задача из разряда тех, которые служат спасательным кругом плавающему студенту. На природе сонное царство середины июля, поэтому самое время устроиться с ноутбуком на пляже. Ранним утром заиграл солнечный зайчик теории, чтобы в скором времени сфокусироваться на практике, которая, несмотря на заявленную лёгкость, содержит осколки стекла в песке. В этой связи рекомендую добросовестно рассмотреть немногочисленные примеры этой странички. Для решения практических заданий необходимо уметь находить производные и понимать материал статьи Интервалы монотонности и экстремумы функции.

Сначала коротко о главном. На уроке о непрерывности функции я приводил определение непрерывности в точке и непрерывности на интервале. Образцово-показательное поведение функции на отрезке формулируется похожим образом. Функция   непрерывна на отрезке   если:

1) она непрерывна на интервале  ; 2) непрерывна в точке   справа и в точке   слева.

Во втором пункте речь зашла о так называемой односторонней непрерывности функции в точке. Существует несколько подходов к её определению, но я буду придерживаться начатой ранее линии:

Функция   непрерывна в точке   справа, если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке:  . Она же непрерывна в точке   слева, если определена в данной точке и её левосторонний предел равен значению в этой точке: 

Представьте, что зелёные точки – это гвозди, на которых закреплена волшебная резинка:

Мысленно возьмите красную линию в руки. Очевидно, что как бы далеко мы не растягивали график вверх и вниз (вдоль оси  ), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне. Таким образом, непрерывная на отрезке функция ограничена на нём. В курсе матанализа этот вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса. …Многих раздражает, что в математике нудно обосновываются элементарные утверждения, однако в этом есть важный смысл. Предположим, некий житель махрового средневековья вытягивал график в небо за пределы видимости вот это вставляло. До изобретения телескопа ограниченность функции в космосе была вовсе не очевидна! Действительно, откуда вы знаете, что нас ждёт за горизонтом? Ведь когда-то и Земля считалась плоской, поэтому сегодня даже обыденная телепортация требует доказательства =)

Согласно второй теореме Вейерштрасса, непрерывная на отрезке   функция достигает своей точной верхней грани   и своей точной нижней грани  .

Число   также называют максимальным значением функции на отрезке и обозначают через  , а число   – минимальным значением функции на отрезке с пометкой  .

В нашем случае: 

Примечание: в теории распространены записи  .

Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка.

Важно! Как уже заострялось внимание в статье об экстремумах функции, наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ, что максимум функции и минимум функции. Так, в рассматриваемом примере число   является минимумом функции, но не минимальным значением.

Кстати, а что происходит вне отрезка  ? Да хоть потоп, в контексте рассматриваемой задачи это нас совершенно не интересует. Задание предполагает лишь нахождение двух чисел   и всё!

Более того, решение чисто аналитическое, следовательно, чертежа делать не надо!

Алгоритм лежит на поверхности и напрашивается из приведённого рисунка:

1) Находим значения функции в критических точках, которые принадлежат данному отрезку.

Ловите ещё одну плюшку: здесь отпадает необходимость проверять достаточное условие экстремума, поскольку, как только что было показано, наличие минимума или максимума ещё не гарантирует, что там минимальное или максимальное значение. Демонстрационная функция достигает максимума   и волей судьбы это же число является наибольшим значением функции на отрезке  . Но, понятно, такое совпадение имеет место далеко не всегда.

Итак, на первом шаге быстрее и проще вычислить значения функции в критических точках, принадлежащих отрезку, не заморачиваясь есть в них экстремумы или нет.

2) Вычисляем значения функции на концах отрезка.

3) Среди найденных в 1-м и 2-м пунктах значений функции выбираем самое маленькое и самое большое число, записываем ответ.

Садимся на берег синего моря и бьём пятками по мелководью:

Пример 1

Найти наибольшее и наименьшее значения функции   на отрезке 

Решение: 1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:  

Полученное квадратное уравнение имеет два действительных корня:  – критические точки.

Ещё раз подчёркиваю, что нас не интересует, есть в них максимумы/минимумы или нет.

Первая критическая точка принадлежит данному отрезку:  А вот вторая – нет:  , поэтому про неё сразу забываем.

Вычислим значение функции в нужной точке:

Итоговый результат я выделил жирным цветом, при оформлении задания в тетради его удобно обвести в кружок простым карандашом или пометить как-то по-другому.

2) Вычислим значения функции  на концах отрезка:

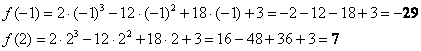
Результаты опять каким-либо образом выделяем.

3) Дело сделано, среди «жирных» чисел выбираем наибольшее и наименьшее.

Ответ: 

Критическое значение   на поверку оказалось точкой максимума, но об этом нас никто не спрашивал. Впрочем, для саморазвития можете устно подмечать такие факты.

Пример 2

Найти наибольшее и наименьшее значения функции   на отрезке 

Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.

В рассматриваемой задаче очень важно не допускать вычислительных ошибок, так как рецензент немедленно посмотрит, сами догадываетесь куда.

Другой существенный момент касается пункта №1.

Во-первых, критических точек может не оказаться вообще. Это очень хорошо – меньше вычислений. Просто записываем вывод: «критические точки отсутствуют» и переходим ко второму пункту алгоритма.

Во-вторых, все критические точки (одна, две или бОльшее количество) могут не принадлежать отрезку. Замечательно. Пишем следующее: «критические точки (а) не принадлежат (ит) рассматриваемому отрезку». Находить какие-то значения функции здесь, разумеется, тоже не надо.

В моей коллекции есть и те и те примеры, но они унылы как бескрайние просторы Сахары. По сути, всё задание сводится к нахождению двух значений функции на концах интервала. Гораздо интереснее снять кепки, солнечные очки и отправиться играть в пляжный футбол:

Пример 3

Найти наибольшее и наименьшее значения функции на заданном отрезке

Решение: всё опять начинается дежурной фразой: 1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:  

Да, критических точек тут и правда целая команда:

Первые две точки принадлежат нашему отрезку: 

Но третья оказывается вне игры: 

(надеюсь, все сумели сосчитать  )

Вычислим значения функции в подходящих точках:

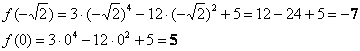
Чтобы не заблудиться в трёх соснах, не забываем выделять результаты,

2) Вычислим значения функции на концах отрезка:

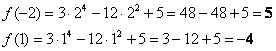
Среди «жирных» чисел выбираем наибольшее и наименьшее значения. Максимальное значение («пятёрка») достигается сразу в двух точках, и это необходимо указать в завершающей записи:

Ответ: 

Время от времени критические точки могут совпадать с одним или даже с обоими концами отрезка, и в этом случае укорачивается второй этап решения. Следующий пример для самостоятельного изучения посвящен как раз такой ситуации:

Пример 4

Найти наибольшее и наименьшее значения функции на заданном отрезке

Примерный образец решения в конце урока.

Иногда техническая трудность рассматриваемого задания состоит в замысловатой производной и громоздких вычислениях:

Пример 5

Найти максимальное и минимальное значения функции на отрезке

Решение: отрезок, надо сказать, творческий, но пример взят из конкретной контрольной работы и ни в коем случае не придуман.

1) Вычислим значения функции в критических точках, которые принадлежат данному отрезку:

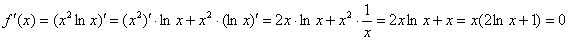
Очевидный корень оказывается не в теме:  .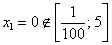

Решаем уравнение: 

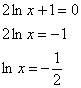
Второй корень принадлежит нашему отрезку: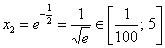 

Если вам не понятно, почему именно такой корень, обязательно обратитесь к школьному учебнику Алгебра и начала анализа 10-11 класс и повторите, что такое логарифм, ибо плох тот студент, который не мечтает овладеть логарифмами.

Дальнейшие вычисления задачи я распишу максимально подробно, но без комментариев. Некоторую информацию о логарифмической функции и свойствах логарифма можно почерпнуть в статье Графики и свойства элементарных функций и методичке по школьным формулам.

Вычислим значение функции во второй критической точке:

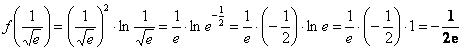
2) Вычислим значения функции на концах отрезка:

3) «Жирные» результаты получены с экспонентами и логарифмами, что существенно затрудняет их сравнение. По сей причине вооружимся калькулятором либо Экселем и вычислим приближённые значения, не забывая, что  :

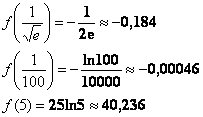
Вот теперь всё понятно.

Ответ: 

Дробно-рациональный экземпляр для самостоятельного решения:

Пример 6

Найти максимальное и минимальное значения функции на отрезке

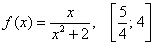
Вычисления в данном случае не менее кропотливы и точно так же потребуют вмешательства калькулятора (если вы, конечно, не вундеркинд). Полное решение и ответ в конце урока.

Стрелки часов приближаются к 9 утра, и побережье потихоньку заполняется всё бОльшим и бОльшим количеством стройных ног. Если честно, не терпится захлопнуть ноут и похулиганить, но всё-таки мужественно разберу нетривиальную вещь:

Пример 7

Найти максимальное и минимальное значения функции на отрезке

Решение:  1) Найдём критические точки. Предварительно можно раскрыть скобки, но не особо сложнее использовать и правило дифференцирования произведения:

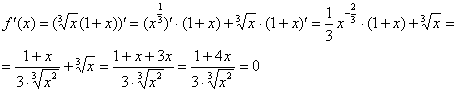
 – критические точки.

Обратите внимание, что точка   обращает знаменатель производной в ноль, но её следует отнести к критическим значениям, поскольку САМА ФУНКЦИЯ определена в данной точке. На этом случае я подробно останавливался в теоретической части и последнем примере урока Интервалы монотонности. Экстремумы функции.

Кроме того, данная точка совпала с правым концом отрезка, а значит, в следующем пункте будет меньше расчётов. В следующем, но не сейчас:

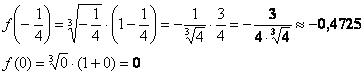
2) Вычислим значения функции на концах отрезка:  уже известно.

Ответ: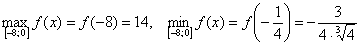 

Раз, два, три, четыре, пять – мне пора верстать.

Скорее всего, вы прочитали данную статью в ненастную погоду, поэтому желаю всем скорейшего летнего загара без зачётки в кармане! …ну или с дипломом на груди… …ой, что-то я не то сказал =)

Решения и ответы:

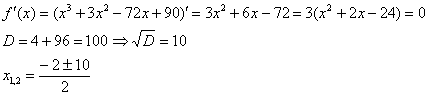
Пример 2: Решение: 1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:     – критические точки. 2)Вычислим значения функции  на концах отрезка: 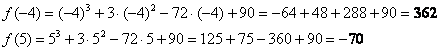Ответ: 

Пример 4: Решение: 1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:     – критические точки. 2) Вычислим значения функции  на концах отрезка:  уже рассчитано в предыдущем пункте.

Ответ: 

Пример 6: Решение: 1) Вычислим значения функции в критических точках, которые принадлежат данному отрезку:  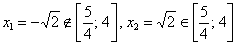– критические точки. 2) Вычислим значения функции  на концах отрезка: Ответ: 

18.Вопрос.Выпуклость и вогнутость прямой. Примеры.

Выпуклость функции, точки перегиба

График функции  , дифференцируемой на интервале  , является на этом интервале выпуклым, если график этой функции в пределах интервала   лежит не выше любой своей касательной (рис. 1).

График функции  , дифференцируемой на интервале  , является на этом интервале вогнутым, если график этой функции в пределах интервала   лежит не ниже любой своей касательной (рис. 2).

Теоремы о выпуклости функции и точках перегиба

Теорема

(Об условиях выпуклости или вогнутости графика функции)

Пусть функция   определена на интервале   и имеет непрерывную, не равную нулю в точке  вторую производную. Тогда, если   всюду на интервале  , то функция имеет вогнутость на этом интервале, если  , то функция имеет выпуклость.

Определение

Точкой перегиба графика функции   называется точка  , разделяющая промежутки выпуклости и вогнутости.

Теорема

(О необходимом условии существования точки перегиба)

Если функция   имеет перегиб в точке  , то   или не существует.

Теорема

(О достаточном условии существования точки перегиба)

Если:

1. первая производная   непрерывна в окрестности точки  ;

2. вторая производная   или не существует в точке  ;

3.  при переходе через точку   меняет свой знак,

тогда в точке   функция   имеет перегиб.

Схема исследования функции на выпуклость, вогнутость

1. Найти вторую производную функции.

2. Найти точки, в которых вторая производная равна нулю или не существует.

3. Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

Пример

Задание. Найти интервалы выпуклости/вогнутости функции 

Решение. Найдем вторую производную заданной функции:

Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение  :

Исследуем знак второй производной слева и справа от полученной точки:

Так как на промежутке   вторая производная  , то на этом промежутке функция  выпукла; в силу того, что на промежутке   вторая производная   - функция вогнута. Так как при переходе через точку   вторая производная сменила знак, то эта точка является точкой перегиба графика функции.

Ответ. Точка   - точка перегиба графика функции.

На промежутке   функция выпукла, на промежутке   функция вогнута.

19 Вопрос. Точки перегиба( необходимые и достаточные условия существования перегиба). Примеры.

Точки перегиба

Определение точки перегиба Рассмотрим функцию y=f(x), которая является непрерывной в точке x0. Функция f(x)  может иметь в этой точке конечную или бесконечную производную f′(x0). Если при переходе через x0 функция меняет направление выпуклости, т.е. существует число δ>0, такое, что на одном из интервалов (x0−δ,x0)  или (x0,x0+δ) функция является выпуклой вверх, а на другом − выпуклой вниз, то x0 называется  точкой перегиба функции y=f(x).  Геометрический смысл точки перегиба состоит в том, что график функции f(x) переходит в этой точке с одной стороны касательной на другую, т.е. кривая и касательная взаимно пересекаются (рисунок 1).  Другое интересное свойство точки перегиба состоит в том, что график функции f(x) в окрестности точки перегиба x0 расположен внутри одной пары вертикальных углов, образованных касательной и нормалью (рисунок 2). Рис.1 Рис.2 Необходимое условие существования точки перегиба Если x0 − точка перегиба функции f(x) и данная функция имеет вторую производную в некоторой окрестности точки x0, причем в точке x0  она непрерывна, тоf′′(x0)=0.Доказательство.  Предположим, что в точке перегиба x0 вторая производная не равна нулю: f′′(x0)≠0. Поскольку она непрерывна при x0, то существует δ-окрестность точки x0, в которой вторая производная сохраняет свой знак, т.е.f′′(x0)<0илиf′′(x0)<0∀x∈(x0−δ,x0+δ). В таком случае функция будет либо строго выпукла вверх (при f′′(x)<0), либо строго выпукла вниз (при f′′(x)>0). Но тогда точка x0 не является точкой перегиба. Следовательно, предположение неверно и вторая производная в точке перегиба должна быть равна нулю. Первое достаточное условие существования точки перегиба Если функция f(x) непрерывна и дифференцируема в точке x0,  имеет вторую производную f′′(x0) в некоторой проколотой  δ-окрестности точки x0 и если вторая производная меняет знак при переходе через точку x0, то x0 является точкой перегиба функции f(x).  Доказательство.  Пусть, например, вторая производная f′′(x)  при переходе через точку x0 меняет знак с плюса на минус. Следовательно , в левой δ-окрестности (x0−δ,x0) выполняется неравенство f′′(x)>0, а в правой δ-окрестности (x0,x0+δ)  справедливо неравенство f′′(x)<0.  В таком случае, согласно достаточным условиям выпуклости, функция f(x) выпукла вниз в левой δ-окрестности точки x0 и выпукла вверх в правой δ-окрестности.  Следовательно, в точке x0 функция меняет направление выпуклости, т.е. c является, по определению, точкой перегиба. Второе достаточное условие существования точки перегиба Пусть f′′(x0)=0, f′′′(x0)≠0. Тогда точка x0 является точкой перегиба функции f(x).  Доказательство.  Поскольку f′′′(x0)≠0, то вторая производная в точке x0  либо строго возрастает (если f′′′(x0)>0), либо строго убывает (если f′′′(x0)<0). Так как f′′(x0)=0, то вторая производная при некотором δ>0 имеет разные знаки в левой и правой δ-окрестности точки x0. Отсюда, на основании предыдущей теоремы, следует что x0 − точка перегиба функции f(x).

Пример 1

Выяснить, является ли точка x=0 точкой перегиба функции f(x)=sinx. Решение. Воспользуемся вторым достаточным признаком существования точки перегиба. Найдем производные синуса до третьего порядка включительно:f′(x)=(sinx)′=cosx,f′′(x)= (cosx)′=−sinx,f′′′(x)=(−sinx)′=−cosx. В точке x=0 вторая и третья производные имеют следующие значения:f′′(0)=−sin0=0,f′′′(0)=−cos0=−1. Таким образом, имеем f′′(x0)=0, f′′′(x0)≠0. Следовательно, по второму достаточному признаку точка x=0 является точкой перегиба.

Пример 2

Найти точки перегиба функцииf(x)=x4−12x3+48x2+12x+1. Решение. Находим производные:f′(x)=(x4−12x3+48x2+12x+1)′= 4x3−36x2+96x+12= 4(x3−9x2+24x+3); f′′(x)=(4(x3−9x2+24x+3)) ′=4(3x2−18x+24)=12(x2−6x+8). Вычисляем корни второй производной:f′′(x)=0,⇒12(x2−6x+8) = 0,⇒x2−6x+8=0,⇒x1=2,x2=4. В данном случае удобно использовать второй достаточный признак существования точки перегиба. Третья производная записывается в видеf′′′(x)=(12(x2−6x+8))′=12(2x−6)=24(x−3). Отсюда сразу видно, что в точках x1=2, x2=4 третья производная не равна нулю. Следовательно, эти точки будут являться точками перегиба.

Пример 3

Найти точки перегиба функции f(x)=x2lnx. Решение. Находим вторую производную:f′(x)=(x2lnx)′=(x2)′lnx+x2(lnx)′= 2xlnx+x2⋅1x=2xlnx+x=x(2lnx+1);f′′(x)=[x(2lnx+1)] ′=x′(2lnx+1)+x(2lnx+1)′=2lnx+1+x⋅2x=2lnx+3 .Решаем уравнение f′′(x)=0:⇒2lnx+3,⇒lnx=−32,⇒x=e−32=1√e3. Вторая производная представляет собой монотонно возрастающую функцию. Поэтому в найденной точке происходит смена знака второй производной. Следовательно, эта точка является точкой перегиба.

Пример 4

Найти точки перегиба функции f(x)=e−x2. Решение. Вычислим производные:f′(x)=(e−x2)′=e−x2⋅(−x2)′=−2xe−x2;f′′(x)= (−2xe−x2)′=(−2x)′e−x2+(−2x)(e−x2)′= −2e−x2−2xe−x2⋅(−2x)=−2e−x2+4x2e−x2=4e−x2(x2−12). Вторая производная равна нулю в следующих точках:f′′(x)=0,⇒4e−x2(x2−12)=0,⇒x2−12=0,⇒x1,2=±1√2. При переходе через точки x1=−1√2, x2=1√2 вторая производная меняет знак (рисунок 3). Следовательно, указанные точки являются точками перегиба. Рис.3 Рис.4

Пример 5

Найти точки перегиба функции f(x)=esinx. Решение. Определим производные заданной функции :f′(x)=(esinx)′=esinx(sinx)′=esinxcosx;f′′(x)= (esinxcosx)′=(esinx)′cosx+esinx(cosx)′= esinxcos2x−esinxsinx=esinx(cos2x−sinx). Точки перегиба должны удовлетворять уравнению  f′′(x)=0. Тогдаf′′(x)=0,⇒esinx(cos2x−sinx)=0,⇒ cos2x−sinx=0,⇒1−sin2x−sinx=0,⇒sin2x+sinx−1=0. Данное тригонометрическое уравнение из школьного курса математики решается с помощью заменыsinx=t.  Следовательно,t2+t−1=0,⇒ D=1−4⋅(−1)=5,⇒t1,2=−1±√5 2.Первый корень t1  со знаком минус в числителе нужно отбросить, поскольку t1<−1. Тогда уравнение имеет следующее единственное решение: t=−1+√52=√5−12,⇒sinx=t=√5−12,⇒ xn=(−1)narcsin√5−12,n∈Z.Итак, мы получили бесконечное множество точек, в которых вторая производная функции равна нулю. В пределах отрезка [0,2π] существуют два решения, равные x1=arcsin√5−12≈0,66;x2=π−arcsin√5−12≈2,48. Остальные решения xn образуются вследствие периодичности синуса и, следовательно, всей функции f(x).  Оба решения x1 и x2 соответствуют правому корню квадратного уравнения. Ясно, что при пересечении корня (в случае двух различных действительных корней) квадратичная функция меняет знак. Поэтому вторая производная, имеющая видf′′(x)=esinx(cos2x−sinx)=esinx(−sin2x−sinx+1), также меняет знак при переходе через точки xn. Отсюда, в соответствии с первым достаточным признаком, вытекает, что все найденные точки xn являются точками перегиба. Схематический вид функции на отрезке [0,2π]  показан на рисунке 4.

20. Вопрос. Понятие первообразной и неопределённого интеграла. Основные свойства неопределённого интеграла. Примеры.

Неопределенный интеграл. Понятие первообразной

Первообразная, основные понятия и определения

Определение

Функция   называется первообразной для функции   на промежутке  , конечном или бесконечном, если функция   дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:

Последнее равенство можно записать через дифференциалы:

   или   

Пример

Функция   является первообразной для функции  , так как

Больше примеров решенийРешение интегралов онлайн

Первообразная   имеет конечную производную, а, следовательно, является непрерывной функцией.

Теорема

(О бесконечном множестве первообразных для функции)

Если функция   является первообразной для функции   на некотором промежутке, то и функция  , где   - произвольная постоянная, также будет первообразной для функции   на рассматриваемом промежутке.

Пример

Известно, что для функции   первообразной является функция  , а, следовательно, и все функции вида   также будут первообразными, так как выполняется равенство  :

Больше примеров решенийРешение интегралов онлайн

Таким образом, если функция   имеет первообразную, то она имеет бесконечное множество первообразных.

Теорема

(Об общем виде первообразной для функции)

Если функции   и   - две любые первообразные функции  , то их разность равна некоторой постоянной, то есть

Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции  , может быть представлена в виде  .

Неопределенный интеграл

Определение

Совокупность всех первообразных функции  , определенных на заданном промежутке, называется неопределенным интегралом от функции   и обозначается символом  . То есть

Знак   называется интегралом,   - подынтегральным выражением,   - подынтегральной функцией, а   - переменной интегрирования.

Операция нахождения первообразной или неопределенного интеграла от функции   называется интегрированием функции  . Интегрирование представляет собой операцию, обратную дифференцированию.

Геометрическая интерпретация неопределенного интеграла

Неопределенный интеграл представляет собой семейство параллельно расположенных кривых  , где каждому конкретному числовому значению постоянной   соответствует определенная кривая из указанного семейства.

График каждой кривой из семейства называется интегральной кривой.

Теорема

Каждая непрерывная на промежутке   функция, имеет на этом интервале первообразную.

Свойства неопределенного интеграла

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению

Пример

2. Производная от неопределенного интеграла равна подынтегральной функции

Пример

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

Пример

4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла

Пример

5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций

Пример

6. Если  , то и  , где функция   - произвольная функция с непрерывной производной.

Пример

Известно, что  , а тогда

Примеры решения задач с интегралами

Интеграл функции является основным понятием интегрального исчисления. Интеграл широко используется при решении целого ряда задач по математике, физике и в других науках. Именно поэтому мы собрали на сайте более 100 примеров решения интегралов и постоянно добавляем новые! Список тем находится в правом меню.

Перед изучением примеров вычисления интегралов советуем вам прочитать теоретический материал по теме: определения, свойства и таблицу интегралов, методы их вычисления и другой материал по интегралам.

Таблица интегралов

Основные ссылки - таблица интегралов и примеры решений (10 шт).

Пример

Задание. Вычислить неопределенный интеграл 

Решение. Для решения данного интеграла не нужно использовать свойства неопределенных интегралов, достаточно формулы интеграла степенной функции:

В нашем случае   , тогда искомый интеграл равен:

Ответ. 

Больше примеров решений →

Метод непосредственного интегрирования

Основные ссылки - метод непосредственного интегрирования и примеры решений (10 шт).

Пример

Задание. Вычислить неопределенный интеграл 

Решение. Преобразуем подынтегральное выражение. Для этого вынесем из знаменателя   за знак интеграла

далее, используя таблицу интегралов (Формула №11), получим

Ответ. 

Больше примеров решений →

Внесение под знак дифференциала

Основные ссылки - внесение под знак дифференциала и примеры решений (10 шт).

Пример

Задание. Вычислить неопределенный интеграл 

Решение. Распишем подынтегральную сумму, используя тригонометрические функции (определение котангенса)

Внесем   под знак дифференциала:

Полученный интеграл можно вычислить, используя табличный интеграл

В результате получим

Ответ. 

Больше примеров решений →

Интегрирование заменой переменной

Основные ссылки - интегрирование заменой переменной и примеры решений (10 шт).

Пример

Задание. Найти неопределенный интеграл 

Решение. Введем замену   и полученный интеграл находим как интеграл от степенной функции:

Сделаем обратную замену

Ответ. 

Больше примеров решений →

Интегрирование по частям

Основные ссылки - интегрирование по частям и примеры решений (10 шт).

Пример

Задание. Найти неопределенный интеграл 

Решение. Воспользуемся методом интегрирования по частям. Для этого положим

Подставим это в формулу для интегрирования по частям, затем воспользуемся формулой интеграла косинуса из таблицы интегралов

Ответ. 

Больше примеров решений →

Метод неопределенных коэффициентов

Основные ссылки - метод неопределенных коэффициентов и примеры решений (10 шт).

Пример

Задание. Разложить рациональную дробь   на простые дроби.

Решение. Так как корнями знаменателя являются значения  ,  , то его можно разложить на множители следующим образом:

А тогда

Искомое разложение имеет вид:

Приводим к общему знаменателю в правой части равенства и приравниваем числители:

Приравнивая коэффициенты, при соответствующих степенях, получаем:

Отсюда, искомое разложение:

Ответ.  

Больше примеров решений →

Интегрирование тригонометрических функций

Основные ссылки - универсальная тригонометрическая подстановка и примеры решений (10 шт).

Пример

Задание. Найти неопределенный интеграл 

Решение. Для вычисления исходного интеграла введем тригонометрическую замену  , тогда

Подставляя это в искомый интеграл, получим

Сделаем обратную замену

Ответ. 

21.Вопрос.Замена переменной в неопределённом интеграле и интегрирование по частям в неопределённом интеграле. Примеры.