Правила Лопиталя. Примеры решений

Представьте стаю воробьёв с выпученными глазами. Нет, это не гром, не ураган и даже не маленький мальчик с рогаткой в руках. Просто в самую гущу птенчиков летит огромное-огромное пушечное ядро. Именно так правила Лопиталя расправляются с пределами, в которых имеет место неопределённость   или   .

Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности, не случайно в сборниках задач, на контрольных работах, зачётах часто встречается устойчивый штамп: «вычислить предел, не пользуясь правилом Лопиталя». Выделенное жирным шрифтом требование можно с чистой совестью приписать и к любому пределу уроков Пределы. Примеры решений, Замечательные пределы. Методы решения пределов, Замечательные эквивалентности, где встречается неопределённость «ноль на ноль» либо «бесконечность на бесконечность». Даже если задание сформулировано коротко – «вычислить пределы», то негласно подразумевается, что вы будете пользоваться всем, чем угодно, но только не правилами Лопиталя.

Всего правил два, и они очень похожи друг на друга, как по сути, так и по способу применения. Кроме непосредственных примеров по теме, мы изучим и дополнительный материал, который будет полезен в ходе дальнейшего изучения математического анализа.

Сразу оговорюсь, что правила будут приведены в лаконичном «практическом» виде, и если вам предстоит сдавать теорию, рекомендую обратиться к учебнику за более строгими выкладками.

Первое правило Лопиталя 

Рассмотрим функции  , которые бесконечно малЫ в некоторой точке  . Если существует предел их отношений  , то в целях устранения неопределённости   можно взять две производные – от числителя и от знаменателя. При этом:  , то есть при дифференцировании числителя и знаменателя значение предела не меняется.

Примечание: предел   тоже должен существовать, в противном случае правило не применимо.

Что следует из вышесказанного?

Во-первых, необходимо уметь находить производные функций, и чем лучше – тем лучше =)

Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного  !!!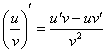

И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость  .

Вернёмся к Примеру 5 первой статьи о пределах, в котором был получен следующий результат: К неопределённости 0:0 применим первое правило Лопиталя: Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!

Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах:

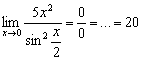
На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:

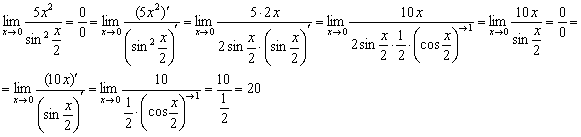
Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции. После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).

Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные, следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам. Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.

Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности.

Второе правило Лопиталя 

Брат-2 борется с двумя спящими восьмёрками  . Аналогично:

Если существует предел отношения бесконечно больших в точке   функций:  , то в целях устранения неопределённости   можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом:  , то есть при дифференцировании числителя и знаменателя значение предела не меняется.

Примечание: предел   должен существовать

Опять же, в различных практических примерах значение   может быть разным, в том числе, бесконечным. Важно, чтобы была неопределённость  .

Проверим Пример №3 первого урока:  . Используем второе правило Лопиталя:

Однако для Примера №2    той же статьи  проверка данным способом будет весьма муторна. Тут придётся использовать правило Лопиталя три раза подряд (экспериментаторы могут попробовать). На самом деле ответ лежит на поверхности и почти мгновенно определяется устно (см. статью Методы решения пределов).

Коль скоро речь зашла о великанах, разберём два каноничных предела:

Пример 1

Вычислить предел 

Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:

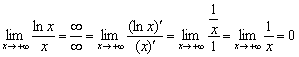
Таким образом, линейная функция более высокого порядка роста, чем логарифм с основанием бОльшим единицы (  и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция   растёт достаточно медленно и её график является более пологим относительно того же «икса».

Пример 2

Вычислить предел 

Ещё один примелькавшийся кадр. В целях устранения неопределённости  , используем правило Лопиталя, причём, два раза подряд:

Показательная функция, с основанием, бОльшим единицы (  и т.д.) более высокого порядка роста, чем степенная функция с положительной степенью.

Похожие пределы встречаются в ходе полного исследования функции, а именно, при нахождении асимптот графиков. Также замечаются они и в некоторых задачах по теории вероятностей. Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.

Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника. В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел.

Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:

Теорема

(Правило Лопиталя).

Пусть функции   и   удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки  , кроме, может быть, самой точки  ;

2)   и   в этой окрестности;

3)  ;

4)   существует конечный или бесконечный.

Тогда существует и  , причем 

Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций.

Замечание

Правило Лопиталя распространяется на случай неопределенности типа   при  .

Применение правила Лопиталя на практике

Пример

Задание. Найти 

Решение. Получим неопределенность и для решения предела воспользуемся правилом Лопиталя.

Ответ. 

Замечание

Правило Лопиталя распространяется и на случай  . Чтобы убедится в этом, достаточно сделать замену   и воспользоваться результатом выше приведенной теоремы.

Замечание

Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми.

Замечание

Хотя правило Лопиталя работает только с неопределенностями   и  , неопределенности других типов могут быть раскрыты с его помощью, если путем преобразований удастся привести изучаемую неопределенность к указанному типу.

Пример

Задание. Найти 

Решение. Получим неопределенность не подходящую под правило Лопиталя, приведем ее к нужному виду и для решения предела воспользуемся правилом Лопиталя.

Ответ. 

14.Вопрос.Раскрытие неопределённостей различных видов.Примеры.

Основные неопределенности и способы их раскрытия

Определение

При вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределенностями.

Основные виды неопределенностей:   ,   ,   ,   ,   ,   , 

Все другие выражения не являются неопределенностями и принимают какое-то конкретное конечное или бесконечное значение.

Раскрытие неопределенностей

Для раскрытия неопределенностей используют следующее:

1. упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;

2. замечательные пределы - первый замечательный предел и второй замечательный предел;

3. правило Лопиталя;

4. эквивалентные бесконечно малые функции.

Основные пределы

1. Первый замечательный предел: 

Пример

Задание. Вычислить предел 

Решение. Получим неопределенность, сделаем замену. При  :  , 

Ответ. 

2. Второй замечательный предел: 

Пример

Задание. Вычислить предел 

Решение. Получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.

Ответ. 

3. Предел частного многочленов на бесконечности:

Пример

Задание. Найти предел 

Решение. 

Ответ. 

4. Предел целой рациональной функции: если   , то 

Пример

Задание. Найти предел функции   в точке 

Решение. 

5. Пределы иррациональных выражений:

а) чтобы найти предел дроби, содержащей иррациональное выражение в случае, когда предел и числителя, и знаменателя равен нулю, надо перенести иррациональность из числителя в знаменатель, или из знаменателя в числитель и после этого сделать необходимые упрощения. Иррациональность переносится с помощью домножения и числителя и знаменателя дроби на выражение, сопряженное к иррациональности.

Пример

Задание. Вычислить предел 

Решение. Получим неопределенность и домножим числитель и знаменатель на выражение, сопряженное к иррациональности.

Ответ. 

15.Вопрос.Условия монотонности дифференцируемой функции. Примеры.

Монотонность функции и ее связь с производной

Монотонность функции, основные понятия и определения

Определение

Функция   называется строго возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.

Пример

Функция   является возрастающей на промежутке  , так как:

для 

Определение

Функция   называется строго убывающей на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.

Пример

Функция   является строго убывающей на промежутке  , так как:

для 

Функция   строго возрастающая или строго убывающая на промежутке называется монотонной на этом промежутке.

Определение

Функция   называется неубывающей на промежутке, если из неравенства   следует неравенство  .

Функция   называется невозрастающей на промежутке, если из неравенства   следует неравенство  .

Связь монотонности функции с ее производной

Теорема

(Об условии возрастания/убывания монотонной функции)

Если производная функции   на некотором промежутке  , то функция   возрастает на этом промежутке; если же   на промежутке  , то функция   убывает на этом промежутке.

Замечание

Обратное утверждение формулируется несколько иначе. Если функция возрастает на промежутке, то  или не существует.

Пример

Задание. Исследовать функцию   на монотонность на всей числовой прямой.

Решение. Найдем производную заданной функции:

Для любого действительного  :  , а поэтому делаем вывод, что заданная функция возрастает на всей действительной оси.

Ответ. Функция   возрастает на всей действительной оси.

16.Вопрос. Экстремумы функций (необходимые и достаточные условия существования) экстремума. Примеры

Понятие экстремума функции

Определение

Точка   называется точкой локального максимума функции  , если существует такая окрестность этой точки, что для всех   из этой окрестности выполняется неравенство:  .

Точка   называется точкой локального минимума функции  , если существует такая окрестность этой точки, что для всех   из этой окрестности  .

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума -локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка   называется точкой строгого локального максимума функции  , если для всех   из окрестности этой точки будет справедливо строгое неравенство  .

Точка   называется точкой строгого локального минимума функции  , если для всех   из окрестности этой точки будет справедливо строгое неравенство  .

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Замечание

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Необходимое условие экстремума

Теорема

(Необходимое условие экстремума)

Если функция   имеет экстремум в точке  , то ее производная   либо равна нулю, либо не существует.

Точки, в которых производная равна нулю:  , называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения  ), либо это точки, в которых производная   не существует.

Замечание

Не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Нужная контрольная на заказ? Цена 400 руб, срок от 1 дня! Скидки и акции!

Быстрый заказГарантии

Первое достаточное условие экстремума

Теорема

(Первое достаточное условие экстремума)

Пусть для функции   выполнены следующие условия:

1. функция непрерывна в окрестности точки  ;

2.  или   не существует;

3. производная   при переходе через точку   меняет свой знак.

Тогда в точке   функция   имеет экстремум, причем это минимум, если при переходе через точку   производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку   производная меняет свой знак с плюса на минус.

Если производная   при переходе через точку   не меняет знак, то экстремума в точке   нет.

Таким образом, для того чтобы исследовать функцию   на экстремум, необходимо:

1. найти производную  ;

2. найти критические точки, то есть такие значения  , в которых   или   не существует;

3. исследовать знак производной слева и справа от каждой критической точки;

4. найти значение функции в экстремальных точках.

Пример

Задание. Исследовать функцию   на экстремум.

Решение. Находим производную заданной функции:

Далее ищем критические точки функции, для этого решаем уравнение  :

Первая производная определена во всех точках. Таким образом, имеем одну критическую точку  . Наносим эту точку на координатную прямую и исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное значение и находим значение производной в выбранной точке, определяем знак полученной величины):

Так как при переходе через точку   производная сменила свой знак с "-" на "+", то в этой точке функция достигает минимума (или минимального значения), причем  .

Замечание. Также можно определить интервалы монотонности функции: так как на интервале  производная  , то на этом интервале функция   является убывающей; на интервале   производная  , значит заданная функция возрастает на нем.

Ответ. 

Второе достаточное условие экстремума

Теорема

(Второе достаточное условие экстремума)

Пусть для функции   выполнены следующие условия:

1. она непрерывна в окрестности точки  ;

2. первая производная   в точке  ;

3.  в точке   .

Тогда в точке   достигается экстремум, причем, если  , то в точке   функция  имеет минимум; если  , то в точке   функция   достигает максимум.

Пример

Задание. Исследовать функцию   на экстремум с помощью второй производной.

Решение. Находим первую производную заданной функции:

Находим точки, в которых первая производная равна нулю:

Вторая производная заданной функции:

В стационарной точке   вторая производная  , а значит, в этой точке функция достигает минимум, причем  .

Ответ. 

17 Вопрос. Наибольшее и наименьшее значение непрерывной на отрезке функции.Примеры.