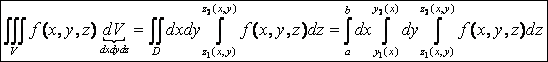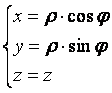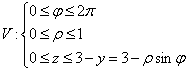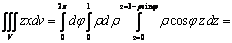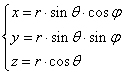3.2. Вычисление тройного интеграла в декартовых координатах

 

Вычисление тройного интеграла сводится к вычислению трехкратного интеграла.

                

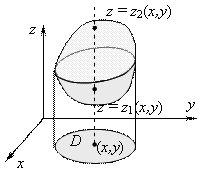
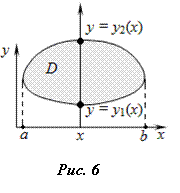
В декартовых координатах область V, правильная в направлении оси OZ, записывается системой неравенств

,

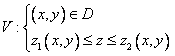где D – это проекция области V на плоскость XOY, а поверхности   и   ограничивают область V соответственно снизу и сверху (Рис. 6).

Если двумерную область D также записать системой 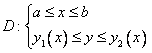неравенств  , то трехмерная область V запишется системой трех неравенств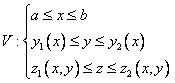  

Тогда тройной интеграл сводится сначала к двойному, а затем к трёхкратному с учётом того, что в декартовых координатах dV = dxdydz;

формула сведения тройного интеграла к трехкратному интегралу имеет следующий вид:

(1)

Существует всего 6 вариантов сведения тройного интеграла к трехкратному в декартовых координатах (в зависимости от выбранного порядка интегрирования).

Пример 1 (вычисление тройного интеграла в декартовых координатах)

Вычислить  , где область V ограничена поверхностями  .

Решение

Запишем область V системой трёх неравенств:

 

Сводим тройной интеграл к трехкратному по формуле (1) в соответствии с системой

неравенств и вычисляем трехкратный интеграл:

  .

 

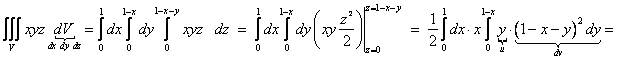
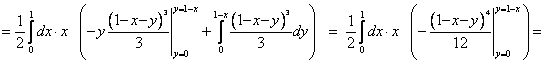
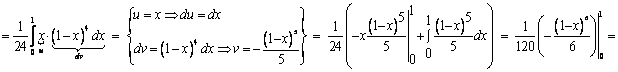
50 Вопрос. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрической системе координат.

Вычисление тройного интеграла в цилиндрических координатах

 

Цилиндрические координаты точки в пространстве XOYZ— это ее полярные координаты   в плоскости XOY и координата z.

Связь между декартовыми и цилиндрическими координатами:

Границы изменения цилиндрических координат для всех точек пространства:  или

                

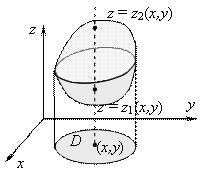
Перевод тройного интеграла к цилиндрическим координатам и сведение его к повторному трехкратному интегралу осуществляется следующими действиями:

 объем V, правильный в направлении оси OZ, проектируется в область   и записывается системой неравенств:

;

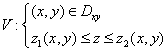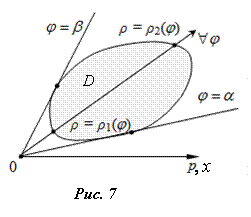
 далее область   записывается неравенствами в полярной системе координат (Рис. 7) и составляется бесконечно малый элемент плоской области в полярных координатах:

,                ;

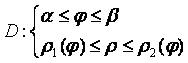 в подынтегральной функции и в пределах интегрирования по z делается переход к переменным   и  :

             

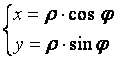
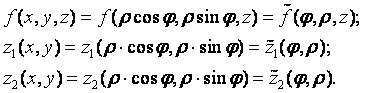
Если выполнить все указанные подстановки, то получится формула вычисления тройного интеграла в цилиндрических координатах:

(2)

Таким образом, бесконечно

Пример 2 (вычисление тройного интеграла в цилиндрических координатах)

Вычислить  , если область V ограничена поверхностями

.

Решение

Строим область V и записываем её системой неравенств в цилиндрических

координатах:

Теперь сводим тройной интеграл к трехкратному в соответствии с системой неравенств и вычисляем его:

    .

 

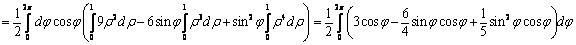
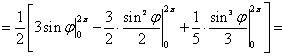
51 Вопрос. Замена переменных в тройном интеграле. Тройной интеграл в сферической системе координат.

Вычисление тройного интеграла в сферических координатах

 

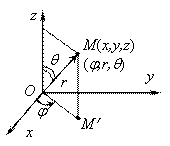
Сферические координаты точки М пространства XOYZ определяются следующим образом (Рис. 8):

r — расстояние точки M от начала координат (длина радиус-вектора точки); r называют сферическим радиусом точки;  — угол между радиус-вектором   и положительным направлением оси OZ;

  — угол между положительным направлением оси OX и проекцией радиус-вектора   на плоскость XOY, отсчитываемый против часовой стрелки (полярный угол).

Границы изменения сферических координат для всех точек пространства:

 или  ,   

 

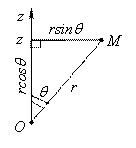
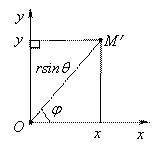
Связь сферических и декартовых координат (выводится геометрически):

 

Замена переменных в тройном интеграле осуществляется в общем случае по формуле, аналогичной формуле замены переменных в двойном интеграле. В частности, при переходе к сферическим координатам эта формула имеет вид:

,

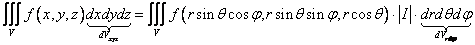I — это функциональный определитель Якоби третьего порядка:

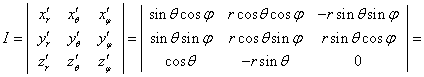
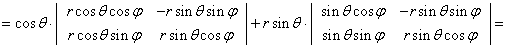
, так как   поэтому  .

Таким образом,  .

Бесконечно малый элемент объема в сферических координатах имеет вид:  ;

формула перевода тройного интеграла к сферическим координатам имеет вид:

(3)

 

Далее тройной интеграл сводится к трехкратному в соответствии с неравенствами для области V в сферических координатах.

Эффективно переводить в сферические координаты тройной интеграл по областям, в границах которых есть сфера.

Пример 3 (вычисление тройного интеграла в сферических координатах)

Вычислить  ,         где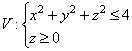 

Решение Область   представляет собой верхнюю половину шара радиуса 2 с центром в начале координат. Запишем неравенствами область V в сферических координатах:

Переводим данный тройной интеграл в сферические координаты по формуле (3) и сводим его к трехкратному интегралу в соответствии с системой неравенств: