1.Определение двойного интеграла. Теорема существования. Его свойства. Пример вычисления.

Определение:

Двойным интегралом от функции   по ограниченной замкнутой области   называется предел интегральной суммы, построенной для функции   при неограниченном увеличении числа разбиений области   на ячейки ( ) и при стягивание каждой ячейки в точку ( ), если такой предел существует и не зависит от способа разбиения области   на ячейки, ни от выбора   в каждой из них.

Теорема существования:

Для всякой непрерывной функции   в ограниченной замкнутой области   существует двойной интеграл: 

Свойства двойного интеграла:

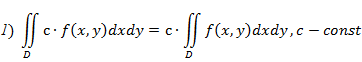
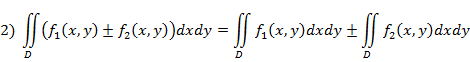
3) Если область   разбить линией на две области   и   такие, что  , а пересечение   и   состоит лишь из линии, их разделяющей, то :

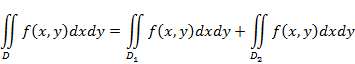
4) Если в области   имеет место неравенство  , то и  . Если в области   функции   и   удовлетворяют неравенству, то и

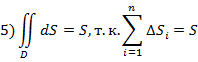
6) Если функция   непрерывна в замкнутой области  , площадь которой  , то  , где   – соответственно наименьшее и наибольшее значения подынтегральной функции в области  .

7) Если функция непрерывна в замкнутой

области  , площадь которой  , то в этой области существует такая точка  , что  . Величину  называют средним значением функции  в области 

Пример вычисления:

Вычислить   в области  , ограниченной кривыми   и  .

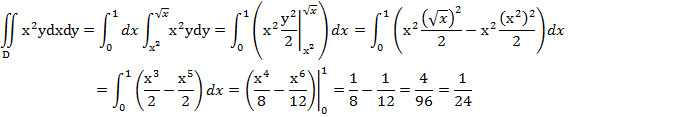
46.Вопрос.Геометрический и физический смысл двойного интеграла и его свойства.

Геометрический и физический смысл двойного интеграла

Рассмотрим две задачи, приводящие к двойному интегралу.

Объем цилиндрического тела

Р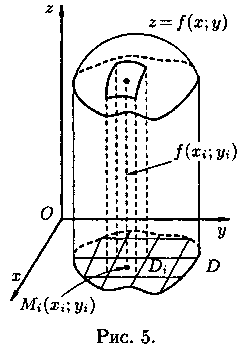 ассмотрим тело, ограниченное сверху поверхностью  снизу - замкнутой  областью D плоскости Оху, с боков - цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 5). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z=ƒ(х;у) на плоскость Оху) произвольным образом на п областей Di, площади которых равны   Рассмотрим цилиндрические столбики с основаниями Di, ограниченные сверху кусками поверхности z=ƒ(х;у)  (на рис. 5 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием D_i через ∆V_i, получим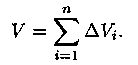

Возьмем на каждой площадке D_i произвольную точку  M_i(x_i;,y_i) и заменим каждый столбик прямым цилиндром с тем же основанием D; и высотой z_i=ƒ(х_i;у_i).

Объем этого цилиндра приближенно равен объему ΔV_i цилиндрического

столбика, т. е. . Тогда получаем:

 

Это равенство тем точнее, чем больше число n и чем меньше размеры «элементарных областей» D_i. Естественно принять предел суммы (7.3) при условии, что число площадок D_i неограниченно увеличивается (n -> ∞), а каждая площадка стягивается в точку (maxd_i-> 0), за объем V цилиндрического тела, т. е.

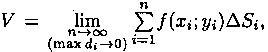
или, согласно равенству (7.2),

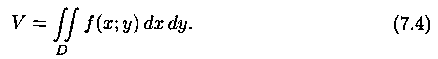
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.

Масса плоской пластинки

Требуется найти массу m плоской пластинки D, зная, что ее поверхностная плотность =(х;у) есть непрерывная функция координат точки (х;у). Разобьем пластинку D на п элементарных частей  площади которых обозначим через ∆S_i. В каждой области D; возьмем произвольную точку М_i(х_i;у_i) и вычислим плотность в ней:

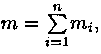Если области D_i достаточно малы, то плотность в каждой точке (х;у) є D_i мало отличается от значения (x_i;y_i). Считая приближенно плотность в каждой точке области D_i постоянной, равной (x_i;y_i), можно найти ее массу   Так как масса m всей пластинки D равна   то для ее  вычисления имеем приближенное равенство

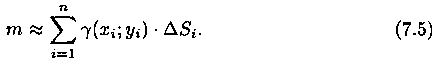
Точное значение массы получим как предел суммы (7.5) при условии n ->∞ и max d_i -> 0:

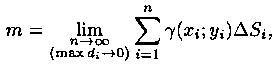
или, согласно равенству (7.2),

Итак, двойной интеграл от функции (x;у) численно равен массе пластинки, если подынтегральную функцию (х;у) считать плотностью этой пластинки в точке (х;у). В этом состоит физический смысл двойного интеграла.