
- •Пример №1
- •Пример №2
- •Пример №3
- •Пример №4
- •Пример №5
- •Пример №6
- •Пример №7
- •Правила Лопиталя. Примеры решений
- •Наибольшее и наименьшее значения функции на отрезке
- •Метод замены переменной в неопределенном интеграле. Примеры решений
- •Интегрирование по частям. Примеры решений
- •16.1.1. Понятие рациональной дроби
- •16.1.2. Простейшие рациональные дроби и их интегрирование
- •16.1.3. Разложение правильной рациональной дроби на простейшие
- •Интегралы от тригонометрических функций. Примеры решений
- •Геометрическии и физический смысл определенного интеграла
- •Формула ньютона-лейбница
- •Формула Ньютона-Лейбница
- •27 Вопрос. Определённый интеграл с переменным верхним пределом. Формула Ньютона Лейбница. Примеры.
- •2.4. Определенный интеграл с переменным верхним пределом.
- •10. Несобственные интегралы
- •10.1 Несобственные интегралы 1 рода
- •10.1.1 Определение и основные свойства
- •10.1.2 Признаки сходимости несобственных интегралов 1 рода
- •3.1. Определение частных производных
- •36.Вопрос.Производные сложных функций нескольких переменных.(рассмотреть случаи одной и нескольких независимых переменных).Примеры.
- •Производная неявно заданной функции.
- •15. Дифференциал. Инвариантность формул первого дифференциала
- •40.Вопрос.Произвольная по направлению. Градиент примеры.
- •41 Вопрос. Локальный экстремум функции двух переменных (определение, необходимое и достаточное условие экстремума).Пример Экстремум функции двух переменных
- •Примеры решения задач
- •Решение.
- •42 Вопрос. Условный экстремум функции двух переменных (Определение ,необходимое и достаточное условие экстремума, функция Лагранжа. Пример. Условные экстремумы и метод множителей Лагранжа
- •43 Вопрос .Глобальный экстремум функции двух переменных(понятие, способ нахождения пример).
- •Метод наименьших квадратов (мнк).
- •1.Определение двойного интеграла. Теорема существования. Его свойства. Пример вычисления.
- •47.Вопрос.Вычисление двойных интегралов в Декартовой системе координат.
- •48 Вопрос. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат.
- •49 Вопрос. Тройной интеграл: его определение,
- •3.2. Вычисление тройного интеграла в декартовых координатах
- •50 Вопрос. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрической системе координат.
- •51 Вопрос. Замена переменных в тройном интеграле. Тройной интеграл в сферической системе координат.
- •52 Вопрос. Приложения кратных интегралов: вычисление объёмов; площадей; статических моментов; центра тяжести; моментов инерции.
- •4.1. Вычисление площади плоской фигуры, занимающей область d
- •4.2. Вычисление объемов с помощью двойного интеграла
- •4.3. Вычисление массы, статических моментов и моментов инерции тонких пластинок
- •4.4. Координаты центра масс пластинки
- •4.5. Приложения тройных интегралов
- •53.Вопрос.Криволинейные интегралы первого рода( понятие, переход к определённому интегралу,свойства,примеры) Криволинейные интегралы. Понятие и примеры решений
- •54.Вопрос.Криволинейные интегралы второго рода(Понятие, переход к определённому интегралу, свойства, примеры)
15. Дифференциал. Инвариантность формул первого дифференциала
Определение
Дифференциалом ![]() в
точке x, соответствующему
в
точке x, соответствующему ![]() называется главная
линейная часть приращения функции.
называется главная
линейная часть приращения функции. ![]() .
.
То
есть если существует производная,
то ![]() при
при ![]() ,
и дифференциал
.
Когда x=const,
то переменной является
и
дифференциал будет линейной функцией.
,
и дифференциал
.
Когда x=const,
то переменной является
и
дифференциал будет линейной функцией.
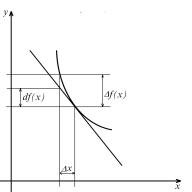
Геометрический смысл дифференциала
|
Дифференциал - приращение, снимаемое с касательной в данной точке. При Если Тогда |
Таблица дифференциалов
|
|
|
Теорема 15.1
Пусть
существуют функции
и ![]() ,
имеющие дифференциалы. Тогда справедливы
равенства:
,
имеющие дифференциалы. Тогда справедливы
равенства:
 ;
;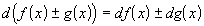 ;
;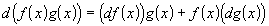 ;
;Если
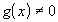 ,
то
,
то 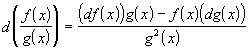 .
.
Доказательство
Пользуясь
теоремой 14.3 о
свойствах производной, умножив равенства
на ![]() .
.
Инвариантность формул первого дифференциала
Пусть
существует сложная функция ![]() ,
и существует ее производная:
,
и существует ее производная: ![]() .
Считая y независимой
переменной, получим формулу дифференциала:
.
Считая y независимой
переменной, получим формулу дифференциала: ![]() .
Теперь, если считать y зависимой
от x,
получим:
.
Теперь, если считать y зависимой
от x,
получим: ![]() ,
т.к.
,
т.к. ![]() .
То есть получается, что формула
дифференциала не
зависит от
типа переменной.
.
То есть получается, что формула
дифференциала не
зависит от
типа переменной.
Не взирая на то, является ли переменная x зависимой или нет, для вычисления дифференциала используется единая формула - инвариантность формул.
Определение
Функция
называется
дифференцируемой в точке x, если ![]() при
.
при
.
Теорема 15.2
Для того, чтобы функция была дифференцируемой в точке x, необходимо и достаточно, чтобы существовала производная в этой точке.
Доказательство
Достаточность
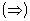 .
Так как существует
.
Так как существует 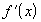 ,
то по теореме 14.2
.
Обозначим
,
то по теореме 14.2
.
Обозначим  ,
это удовлетворяет условию дифференцируемости.
,
это удовлетворяет условию дифференцируемости.Необходимость
 .
По определению дифференцируемости
.
Выразим
.
По определению дифференцируемости
.
Выразим  при
.
Значит, существует предел
при
.
Значит, существует предел 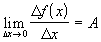 ,
т.е.
,
т.е. 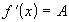
.
40.Вопрос.Произвольная по направлению. Градиент примеры.
Пусть
в некоторой области 3-х мерного пространства
задано скалярное поле ![]() .
Выберем в этой области точку
.
Выберем в этой области точку ![]() .
Если перемещаться из этой точки вдоль
какой-либо линии, то поле будет меняться
от точки к точке. Причем, ясно, что для
различных направлений скорость
изменения
.
Если перемещаться из этой точки вдоль
какой-либо линии, то поле будет меняться
от точки к точке. Причем, ясно, что для
различных направлений скорость
изменения ![]() также
может оказаться различной и должна
характеризовать само поле в рассматриваемой
точке или ее окрестности. При этом, по
смыслу рассуждений, эта величина должна
быть векторной. Рассмотрим строгое
определение этой характеристики на
примере гидромеханической аналогии.
Пусть в пространстве задано скалярное
поле давления жидкости или газа. Поместим
в эту область тело произвольной формы,
ограниченное поверхностью
также
может оказаться различной и должна
характеризовать само поле в рассматриваемой
точке или ее окрестности. При этом, по
смыслу рассуждений, эта величина должна
быть векторной. Рассмотрим строгое
определение этой характеристики на
примере гидромеханической аналогии.
Пусть в пространстве задано скалярное
поле давления жидкости или газа. Поместим
в эту область тело произвольной формы,
ограниченное поверхностью ![]() ,
(рис. 24).
Вычислим суммарую силу
,
(рис. 24).
Вычислим суммарую силу ![]() ,
действующую на тело со стороны среды.
,
действующую на тело со стороны среды.

Рис.24 К определению градиента скалярной функции
Рассмотрим
площадку ![]() ,
содержащую точку
на
поверхности
.
Модуль силы, действующей на площадку
,
равен
,
содержащую точку
на
поверхности
.
Модуль силы, действующей на площадку
,
равен ![]() ,
а направление совпадает с направлением
нормали к поверхности в точке
.
Таким образом, вектор силы
,
а направление совпадает с направлением
нормали к поверхности в точке
.
Таким образом, вектор силы
|
(71) |
Полная сила может быть вычислена интегрированием по поверхности :
|
(72) |
Если
результат (72)
разделить на объем ![]() ,
заключенный внутри поверхности
,
то получившаяся величина
,
заключенный внутри поверхности
,
то получившаяся величина
|
(73) |
будет "средней" силой, действующей со стороны среды на любую точку внутри . Физической причиной этого действия является перепад давлений между различными точками среды.
Способность
поля (в данном случае поля давлений)
оказывать действие на пробное тело
является характеристикой самого поля
и поэтому не должна зависеть на формы
и размеров тела, помещенного в это поле.
Будем стягивать поверхность
к
точке
,
устремляя, таким образом, ![]() и
рассмотрим предел
и
рассмотрим предел
|
(74) |
Если предел (74) существует, то по смыслу рассуждений он определит плотность силы, действующей со стороны поля (давлений) на точечное тело, помещенное в точку и будет характеризовать быстроту изменения поля (перепад давлений) в окрестности этой точки.
Рассмотрим общий случай скалярного поля . Если для поля существует предел (74) при стягивании поверхности к точке , то он называется градиентом поля в этой точке:
|
(75) |
По
определению ![]() является
вектором и вообще, выражение (75),
будучи примененным в каждой точке
области определения поля
,
будет задавать векторное поле градиента
.
является
вектором и вообще, выражение (75),
будучи примененным в каждой точке
области определения поля
,
будет задавать векторное поле градиента
.
Формула
(75)
задает определение
в
форме, независящей от системы координат
- инвариантно. Пользуясь (75),
получим формулу вычисления градиента
скалярного поля в декартовой системе
координат. Тогда, так как вектор нормали ![]() :
:
|
(76) |
Применим к каждому слагаемому (76) формулу Остроградского-Гаусса (3.1):
|
(77) |
Применяя теорему о среднем к правой части (77), получим
|
(78) |
переходя к пределу и сравнивая с определением градиента (75), получим формулу для вычисления градиента в декартовой системе координат:
|
(79) |
Производная
по направлению. Выберем
в пространстве, где задано скалярное
поле
некоторое
направление с помощью единичного
вектора ![]() .
Считая, что этот вектор определяет
координатную ось
.
Считая, что этот вектор определяет
координатную ось ![]() и
пользуясь правилом дифференцирования
сложной функции, вычислим производную
и
пользуясь правилом дифференцирования
сложной функции, вычислим производную
|
(80) |
Полученное
выражение, учитывая, что ![]() -
координаты вектора
,можно
переписать как скалярное произведение
-
координаты вектора
,можно
переписать как скалярное произведение
|
(81) |
Это
выражение (81)
называется производной
по направлению ![]() поля
.
поля
.
Из определения (81) следуют свойства градиента:
 направлен
перпендикулярно к линии уровня
направлен
перпендикулярно к линии уровня  ;
;направлен в сторону наискорейшего возрастания функции ;
Формула (79) позволяет получить следующие свойства и правила вычисления :
1. |
|
(82) |
2. |
|
(83) |
3. |
|
(84) |
Пример 3-8. Вычислить
градиент поля ![]() ,
где
,
где ![]() -
модуль радиус-вектора,
-
модуль радиус-вектора, ![]() .
.
Решение. Согласно выражению (79), получим


Аналогично,  ,
,  и
тогда, складывая вычисленные производные,
получим:
и
тогда, складывая вычисленные производные,
получим:
 или
в бескоординатной форме
или
в бескоординатной форме

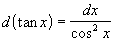
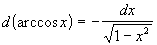
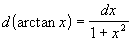
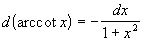










 (сложное
поле)
(сложное
поле)