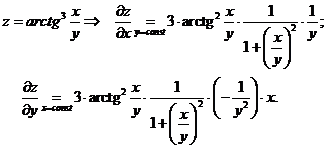3.1. Определение частных производных

Рассмотрим функцию  , непрерывную в точке   и некоторой её окрестности.

 – это частное приращение функции z(x,y) по аргументу x;

– это частное приращение функции z(x,y)  по аргументу у;

 – это частная производная функции z(x,y)  по аргументу x;

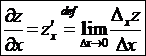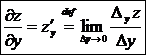 – это частная производная функции (x,y) z по аргументу у.

ОПРЕДЕЛЕНИЕ ЧАСТНОЙ ПРОИЗВОДНОЙ ФНП

Частной производной функции нескольких переменных по одному из её аргументов называется конечный предел отношения частного приращения функции по этому аргументу к приращению аргумента при условии, что приращение аргумента стремится к нулю

 

3.2. Правило вычисления частных производных

Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование как функции одного аргумента, используя известные для нее правила дифференцирования и таблицу производных.

Примеры (вычисления частных производных)

1.       

 

 

3.3. Геометрический смысл частных производных функциии 2-х переменных

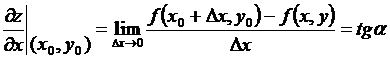 –  это есть угловой коэффициент касательной к сечению поверхности   плоскостью y=y₀, рис. 10.

 – это есть угловой коэффициент касательной к сечению поверхности   плоскостью х=х₀, рис.11. 

 

Примеры (на геометрический смысл частных производных)

1.      Какой угол образует с положительным направлением оси абсцисс касательная к линии  в точке M₀(2;4;5)?

Решение:

Ответ:  .

3.4. Механический смысл частных производных (В чем состоит механический смысл частных производных?)

Если  , то

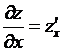  –  это скорость изменения функции z по ее аргументу x при фиксированном значении аргумента y;

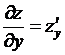  –  это скорость изменения функции z по ее аргументу y при фиксированном значении аргумента x.

3.5. Частные производные высших порядков

Пусть функция z = f(x,y) имеет в точке (x,y) и её окрестности имеет непрерывные частные производные первого порядка 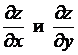 . Так как   являются функциями тех же самых аргументов x и y, то их можно дифференцировать по x и по y. При этом возможны следующие четыре варианта:

эти частные производные называются частными производными второго порядка от функции  ; при этом   и   называются смешанными частными производными второго порядка.

 

Аналогично определяются частные производные ΙΙΙ-го порядка:

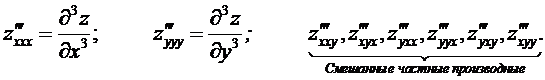
Примеры (повторного дифференцирования ФНП)

1. Дана ФНП  . Вычислить все её частные производные второго порядка.

 

Решение:

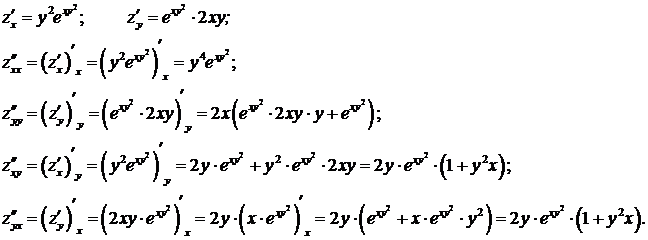Из примера видно, что  .

 

Основное свойство смешанных частных производных

Если функция z = f(x,y) и её частные производные  , , ,  определены и непрерывны в точке (x;y) и некоторой её окрестности, то в этой точке

,

то есть смешанные частные производные при условии их непрерывности не зависят от последовательности, в которой производится дифференцирование.

Свойство справедливо для функций любого числа аргументов и для смешанных частных производных любого порядка.

Например,  , если эти частные производные непрерывны.

 

34 Вопрос. Дифференцируемость функции нескольких переменных, необходимые и достаточные условия дифференцируемости. Дифференциал функции нескольких переменных.

4. Дифференцируемость функции нескольких переменных в точке. Достаточное условие дифференцируемости функции

Опр: Функция   определенная в окрестности   называется дифференцируемой в этой точке, если ее приращение Δf в  :

= – = +  , что 

Необходимое условие дифференцируемости:

Если функция   дифференцируема в  , то,

1.Она непрерывна в этой окрестности.

2.Существуют частные производные  , i=1,...,m; причем 

Док-во:

Если дифф.,то  = +  +  ,

lim   lim   (при   и )=

Следовательно,  непрерывна в  .

Докажем, что в   сущ.  =0.

– = + , НО lim  =0,  . Значит, lim  =0 (аналог предела по направлению для функции m переменных)

– = + , где  .

( – )/

Тогда в пределе при   существует  что и требовалось доказать.

Достаточное условие дифференцируемости

Пусть существуют и непрерывны  для функции   в  для функции m переменных. Тогда   дифференцируема в .

Док-во.

Доказываем при m=2, (в общем случае аналогично, но более громоздко)

Т.к. , непрерывны в  , то они определены в  => f(x,y) определена в . Рассмотрим ∆х, ∆у такие, что   принадлежит  .

– – + =

Рассмотрим   — дифф. по х на  , 

 – дифф. по у на  , . По теоремеЛагранжа:

=  +

(или наоборот, в зависимости от знаков ∆х,∆у)

Пусть  и  . В силу непрерывности соответствующих функций двух переменных:

,  ; 

; 

;  , можно считать, что

+(B+ +

 

Доопределим: x'(0,0)= ,  (0,0)=

 

По теореме о двух милиционерах следует, что функции  ,x' непрерывны по ∆х,∆y в  (0,0), (x,у) и  (х,у)

непрерывны по х и у в  (0,0), по теореме о суперпозиции непрерывных функций.

   

   .

, то есть   умножается на функцию от ∆х,∆y, которая стремится к нулю, при 

. что и требовалось доказать.

Полный дифференциал сложной функции

 

Найдем полный дифференциал сложной функции, определяемой равенствами (7) и (8). По формуле (4) dz(х, у) =  dx +  dу, а частные производные   и   сложной функции определяются равенствами (11) и (12), соответственно. Следовательно,

 

dz(х, у) =  +  .

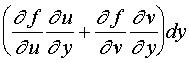Преобразуем правую часть: 

 

                    .

 

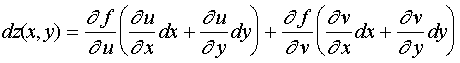Так как 

,     , 

 

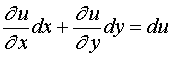 то последнее равенство примет вид: 

                                              dz =   du +  dу                                 (13)               

 

Сравнивая формулы (13) и (4), можно сказать, что полный дифференциал функции z = f(u, v)  имеет один и тот же вид независимо от того, являются ли ее аргументы независимыми переменными или функциями независимых переменных. Этот факт называют свойством инвариантности дифференциала первого порядка. Таким образом, нами установлено, что функции нескольких переменных обладают свойством инвариантности формы первого дифференциала.

Пример 6. Найти полный дифференциал сложной функции w = u/v,  если    u = x, v = x² + y² + z² .

Решение. По формуле нахождения дифференциала частного:

 

 

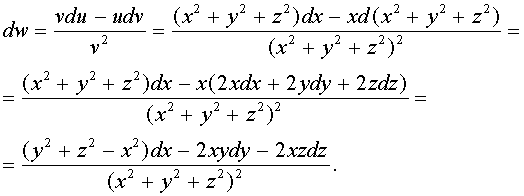
Отсюда, сравнивая с формулой (4), заключаем, что

  

     

.

 

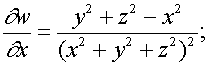
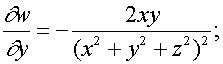
35 Вопрос. Касательная плоскость и нормаль к поверхности, их уравнения. Геометрический смысл дифференциала.

Краткая справка

Задача № 7. Касательная плоскость и нормаль к поверхности.

Касательная плоскость к поверхности в её точке   (точка касания) есть плоскость, проходящая через  и содержащая в себе все касательные, проведённые в точке   ко всевозможным кривым, проведённым на поверхности через точку 

Нормалью к поверхности в точке   называется прямая, проходящая через точку   и перпендикулярная к касательной плоскости, проведённой в этой точке.

Если уравнение поверхности имеет вид F(x, y, z)=0, то уравнение касательной плоскости в точке   имеет вид:

Уравнение нормали к этой поверхности в точке   есть

В случае явного задания поверхности уравнением (8.1) и (8.2) примут вид

Пример решений

Пример 7.1. Найти уравнение касательной плоскости и уравнение нормали к поверхности  в точке 

Решение: Имеем

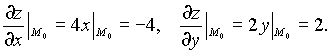
Тогда, согласно (8.3) уравнение касательной плоскости к данной поверхности в указанной точке будет иметь вид: z - 6 = - 4(x + 1) + 2(y - 2), то есть 4x - 2y + z + 2 = 0, а уравнение нормали

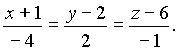
Пример 7.2. Найти уравнение касательной плоскости и нормали к косинусу

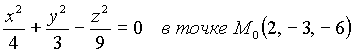
Решение. Имеем

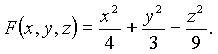
Тогда

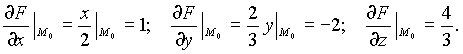
Уравнение касательной плоскости запишем в виде

Геометрический смысл дифференциала.

Дифференциал функции f(x) в точке x₀ равен приращению, которое получает ордината касательной к кривой y = f(x) с абсциссой в точке x₀ при переходе из точки касания в точку с абсциссой x₀+Δx.