
- •Пример №1
- •Пример №2
- •Пример №3
- •Пример №4
- •Пример №5
- •Пример №6
- •Пример №7
- •Правила Лопиталя. Примеры решений
- •Наибольшее и наименьшее значения функции на отрезке
- •Метод замены переменной в неопределенном интеграле. Примеры решений
- •Интегрирование по частям. Примеры решений
- •16.1.1. Понятие рациональной дроби
- •16.1.2. Простейшие рациональные дроби и их интегрирование
- •16.1.3. Разложение правильной рациональной дроби на простейшие
- •Интегралы от тригонометрических функций. Примеры решений
- •Геометрическии и физический смысл определенного интеграла
- •Формула ньютона-лейбница
- •Формула Ньютона-Лейбница
- •27 Вопрос. Определённый интеграл с переменным верхним пределом. Формула Ньютона Лейбница. Примеры.
- •2.4. Определенный интеграл с переменным верхним пределом.
- •10. Несобственные интегралы
- •10.1 Несобственные интегралы 1 рода
- •10.1.1 Определение и основные свойства
- •10.1.2 Признаки сходимости несобственных интегралов 1 рода
- •3.1. Определение частных производных
- •36.Вопрос.Производные сложных функций нескольких переменных.(рассмотреть случаи одной и нескольких независимых переменных).Примеры.
- •Производная неявно заданной функции.
- •15. Дифференциал. Инвариантность формул первого дифференциала
- •40.Вопрос.Произвольная по направлению. Градиент примеры.
- •41 Вопрос. Локальный экстремум функции двух переменных (определение, необходимое и достаточное условие экстремума).Пример Экстремум функции двух переменных
- •Примеры решения задач
- •Решение.
- •42 Вопрос. Условный экстремум функции двух переменных (Определение ,необходимое и достаточное условие экстремума, функция Лагранжа. Пример. Условные экстремумы и метод множителей Лагранжа
- •43 Вопрос .Глобальный экстремум функции двух переменных(понятие, способ нахождения пример).
- •Метод наименьших квадратов (мнк).
- •1.Определение двойного интеграла. Теорема существования. Его свойства. Пример вычисления.
- •47.Вопрос.Вычисление двойных интегралов в Декартовой системе координат.
- •48 Вопрос. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат.
- •49 Вопрос. Тройной интеграл: его определение,
- •3.2. Вычисление тройного интеграла в декартовых координатах
- •50 Вопрос. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрической системе координат.
- •51 Вопрос. Замена переменных в тройном интеграле. Тройной интеграл в сферической системе координат.
- •52 Вопрос. Приложения кратных интегралов: вычисление объёмов; площадей; статических моментов; центра тяжести; моментов инерции.
- •4.1. Вычисление площади плоской фигуры, занимающей область d
- •4.2. Вычисление объемов с помощью двойного интеграла
- •4.3. Вычисление массы, статических моментов и моментов инерции тонких пластинок
- •4.4. Координаты центра масс пластинки
- •4.5. Приложения тройных интегралов
- •53.Вопрос.Криволинейные интегралы первого рода( понятие, переход к определённому интегралу,свойства,примеры) Криволинейные интегралы. Понятие и примеры решений
- •54.Вопрос.Криволинейные интегралы второго рода(Понятие, переход к определённому интегралу, свойства, примеры)
10.1.2 Признаки сходимости несобственных интегралов 1 рода
Теорема(первый признак сравнения). Пусть f(x), g(x) - непрерывны при x>a, причем $0<f(x)a$. Тогда</f(x)
1. Если интеграл
∫+∞ag(x)dx
сходится, то сходится и интеграл
∫+∞af(x)dx.
2. Если интеграл
∫+∞af(x)dx
расходится, то расходится и интеграл
∫+∞ag(x)dx.
Теорема(второй признак сравнения). Пусть f(x), g(x) - непрерывны и положительны при x>a, причем существует конечный предел
θ=limx→+∞f(x)g(x),θ≠0,+∞.
Тогда интегралы
∫+∞af(x)dx,∫+∞ag(x)dx
сходятся или расходятся одновременно.
Пример.
Задачи.
Пример
1.
Интеграл
|
***
Пример
2.
Интеграл
|
***
Пример
3.
Интеграл
при |
***
Пример
4.
Несобственный интеграл
|
***
Пример
5.
Несобственный интеграл
|
30.Вопрос.Несобственные интегралы второго рода (определения, примеры)
Несобственные интегралы второго рода
Определение. Пусть f(x)
задана на полуинтервале [a,b) и ![]() Пусть
далее для всякого
Пусть
далее для всякого ![]() существует
интеграл
существует
интеграл ![]() Предел
Предел ![]() называется
несобственным интегралом второго рода
(интегралом от неограниченной функции)
и обозначается
называется
несобственным интегралом второго рода
(интегралом от неограниченной функции)
и обозначается ![]() Если
существует
и конечен, то несобственный интеграл
второго рода называется сходящимся,
если же он не существует или
равен бесконечности, то несобственный
интеграл второго рода называется
расходящимся.
Аналогично
определяются несобственные интегралы
второго рода в случаях, когда подынтегральная
функция бесконечно большая на нижнем
пределе, во внутренней точке отрезка
[a,b], на верхнем и нижнем пределах
одновременно. Мы рассмотрим случай
особенности на верхнем пределе. Для
остальных вариантов предлагается
проделать это самостоятельно.
Пример. Рассмотрим
Если
существует
и конечен, то несобственный интеграл
второго рода называется сходящимся,
если же он не существует или
равен бесконечности, то несобственный
интеграл второго рода называется
расходящимся.
Аналогично
определяются несобственные интегралы
второго рода в случаях, когда подынтегральная
функция бесконечно большая на нижнем
пределе, во внутренней точке отрезка
[a,b], на верхнем и нижнем пределах
одновременно. Мы рассмотрим случай
особенности на верхнем пределе. Для
остальных вариантов предлагается
проделать это самостоятельно.
Пример. Рассмотрим ![]() .
Пусть
.
Пусть ![]() Тогда
Тогда ![]()
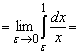
![]() Таким
образом, рассмотренный интеграл
при
Таким
образом, рассмотренный интеграл
при ![]() расходится.
Пусть теперь
расходится.
Пусть теперь ![]() Тогда
Тогда

и
мы окончательно получили, что
рассматриваемый интеграл при ![]() сходится
и при
сходится
и при ![]() расходится.
Интегралы
,
расходится.
Интегралы
, ![]() ,
, ![]() используются
в признаке сравнения в качестве
эталонных.
Аналогично
случаю несобственных интегралов первого
рода формулируются и доказываются
критерий Коши и признаки сравнения для
несобственных интегралов второго
рода.
Теорема
2.7.(Критерий
Коши). Несобственный интеграл второго
рода сходится тогда и только тогда,
когда для всякого ε>0 существует
используются
в признаке сравнения в качестве
эталонных.
Аналогично
случаю несобственных интегралов первого
рода формулируются и доказываются
критерий Коши и признаки сравнения для
несобственных интегралов второго
рода.
Теорема
2.7.(Критерий
Коши). Несобственный интеграл второго
рода сходится тогда и только тогда,
когда для всякого ε>0 существует ![]() такое,
что для всех
такое,
что для всех ![]() выполняется
неравенство
выполняется
неравенство  Доказательство
этого результата опустим.
Теорема
2.8. Пусть
для всякого
Доказательство
этого результата опустим.
Теорема
2.8. Пусть
для всякого ![]() выполнено
неравенство
выполнено
неравенство ![]() .
Тогда, если интеграл
.
Тогда, если интеграл ![]() сходится,
то интеграл
сходится,
то интеграл ![]() сходится,
а если интеграл
расходится,
то интеграл
расходится.
Доказательство опустим.
Теорема
2.9. Если
f(x) и g(x)бесконечно большие одного порядка
роста, то есть
сходится,
а если интеграл
расходится,
то интеграл
расходится.
Доказательство опустим.
Теорема
2.9. Если
f(x) и g(x)бесконечно большие одного порядка
роста, то есть ![]() ,
то интегралы
и
либо
оба сходятся, либо оба расходятся.
,
то интегралы
и
либо
оба сходятся, либо оба расходятся.
Примеры 1.
Выяснить сходимость интеграла ![]() По
определению имеем
По
определению имеем
![]()
2.
Выяснить сходимость интеграла ![]() Подынтегральная
функция имеет особенность в
точках
Подынтегральная
функция имеет особенность в
точках ![]() и
и ![]() Разбиваем
интеграл на два
Разбиваем
интеграл на два
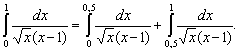
Первый
из этих интегралов сходится, так как
порядок роста подынтегральной функции
при ![]() относительно
1/x равен ½ , а второй расходится, так как
порядок роста подынтегральной функции
при
относительно
1/x равен ½ , а второй расходится, так как
порядок роста подынтегральной функции
при ![]() относительно
относительно ![]() равен
1.
равен
1.
31.Вопрос.Геометрические приложения определённого интеграла площадь плоской фигуры,
длина дуги кривой, вычисление объёмов тел превращения .Примеры.
1. Вычисление площади плоской фигуры
1.1.
Пусть функция ![]() непрерывна
и неотрицательна на отрезке [a, b]. Тогда
площадь фигуры, ограниченной осью ОХ,
отрезками прямых x = a, x = b и
графиком функции
непрерывна
и неотрицательна на отрезке [a, b]. Тогда
площадь фигуры, ограниченной осью ОХ,
отрезками прямых x = a, x = b и
графиком функции ![]() ,
может быть вычислена по формуле
,
может быть вычислена по формуле 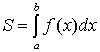 (см.
10.1 рис. 1).
(см.
10.1 рис. 1).
1.2.
Если ![]() на
отрезке [a, b],
на
отрезке [a, b], ![]() непрерывные
функции, то площадь фигуры, ограниченной
прямыми х
= а, x = b,
графиками функций
непрерывные
функции, то площадь фигуры, ограниченной
прямыми х
= а, x = b,
графиками функций ![]() вычисляется
по формуле
вычисляется
по формуле 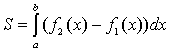 (рис.
10).
(рис.
10).
1.3.
Если функция
на
отрезке [a, b]
принимает значения разных знаков,
то площадь фигуры, заключенная между
кривой
и
осью ![]() , равна
, равна  (рис.
11).
(рис.
11).


Рис. 10 Рис. 11
П
р и м е р 15. Вычислить площадь
фигуры, ограниченной графиками
функций ![]() и
и ![]() .
.
Решение. Вычислим координаты точек пересечения графиков этих функций. Для этого решим систему
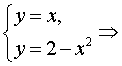
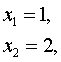


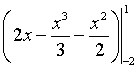 =
=
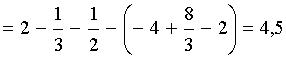 кв.
ед. (рис. 12).
кв.
ед. (рис. 12).
1.4.
При вычислении площади криволинейной
трапеции, в случае когда верхняя
граница задана параметрическими
уравнениями 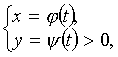 t в
формуле
t в
формуле 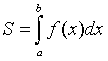 надо
сделать замену переменной, положив
надо
сделать замену переменной, положив ![]() ,
тогда получим
,
тогда получим 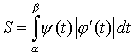 ,
где и значения
параметра t,
соответствующие значениям x=a и x=b,
т. е.
,
где и значения
параметра t,
соответствующие значениям x=a и x=b,
т. е. ![]() .
.
П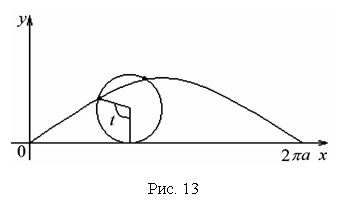 р и м е р 16. Найти пло-щадь фигуры,
ограниченной одной
аркой циклоиды
р и м е р 16. Найти пло-щадь фигуры,
ограниченной одной
аркой циклоиды 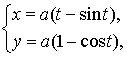
![]() и
осью
.
и
осью
.
Замечание. Циклоида плоская кривая, которую описывает точка М окружности радиуса a, катящаяся без скольжения по прямой линии (рис. 13).
Решение. Искомая площадь
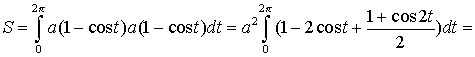
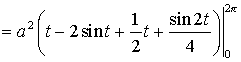
![]() ;
; ![]() .
.
П
р и м е р 17. Вычислить площадь
фигуры, ограниченной линиями, заданными
уравнениями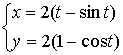 , y = 2
, y = 2 ![]() .
.
Решение. Из условия задачи следует, что y>0 при любом t. Решим неравенство
![]() ,
,![]() ,
,![]() .
.
Но
по условию ![]() .
При k = 0
.
При k = 0
2 t 3 2 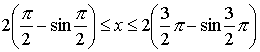 ,
, ![]() .
.
При ![]() x не
будет принадлежать интервалу
x не
будет принадлежать интервалу ![]() .
Фактически нужно вычислить площадь
фигуры, заключенной между прямой y = 2
и частью циклоиды, расположенной выше
этой прямой (рис. 14).
.
Фактически нужно вычислить площадь
фигуры, заключенной между прямой y = 2
и частью циклоиды, расположенной выше
этой прямой (рис. 14).
Искомая площадь
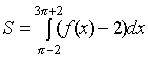
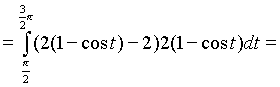

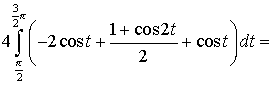
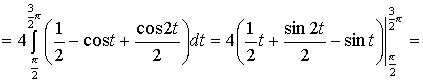
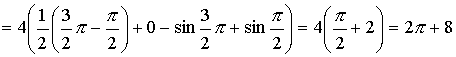 .
.
2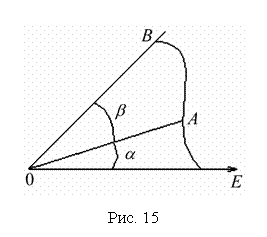 . Вычисление
площади криволинейного сектора. Пусть
кривая AB зада-на
в полярных координатах уравнением
. Вычисление
площади криволинейного сектора. Пусть
кривая AB зада-на
в полярных координатах уравнением ![]() ,
, ![]() ,
причем
,
причем ![]() непрерывная
и неотрицательная на отрезке
непрерывная
и неотрицательная на отрезке ![]() функция.
Фигуру, ограниченную кривой AB и
двумя полярными радиусами, составляющими
с полярной осью углы
функция.
Фигуру, ограниченную кривой AB и
двумя полярными радиусами, составляющими
с полярной осью углы ![]() ,
будем называть криволинейным
сектором.
,
будем называть криволинейным
сектором.
Площадь криволинейного сектора может быть вычислена по формуле
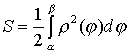 . (27)
. (27)
П
р и м е р 18. Вычислить площадь
фигуры, ограниченной кривой ![]() (4-лепестковая
роза рис.
16).
(4-лепестковая
роза рис.
16).
Решение.
Меняя непрерывно от
0 до ![]() ,
можно построить первый лепесток. Составим
таблицу значений функций (табл. 3).
,
можно построить первый лепесток. Составим
таблицу значений функций (табл. 3).
Таблица 3
|
0 |
|
|
|
|
|
|
|
0 |
2 |
|
4 |
|
2 |
0 |
В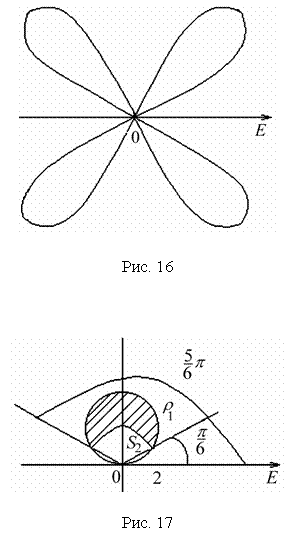 ычислим
площадь одного лепестка по формуле (27)
ычислим
площадь одного лепестка по формуле (27)
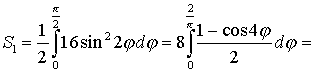
 .
.
Следовательно, площадь всех лепестков
![]() .
.
П
р и м е р 19. Вычислить площадь
фигуры, ограниченной линиями, заданными
уравнениями ![]() ,
, ![]() (рис.
17).
(рис.
17).
Решение.
При изменении
от
0 до ![]() полярный
радиус
полярный
радиус ![]() опишет
кривую, изображенную на (рис. 17),
опишет
кривую, изображенную на (рис. 17), ![]() при
при ![]() .
Уравнение
есть
уравнение окружности с центром в точке
0 радиуса 2. Найдем, при каких
линии
пересекаются. Для этого решим систему
.
Уравнение
есть
уравнение окружности с центром в точке
0 радиуса 2. Найдем, при каких
линии
пересекаются. Для этого решим систему
 ;
;
![]() ;
;  ;
; ![]() .
.
И тогда искомая площадь
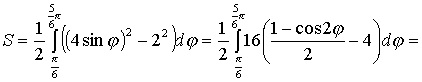
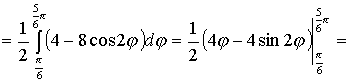
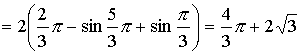 ;
;
 .
.
3. Вычисление длины дуги плоской кривой
3.1 Если функция y = f(x) непрерывна вместе с её производной f'(x) на отрезке [a, b], то длина дуги AB, где A(a,f(a)), B(b, f(b)), выражается формулой
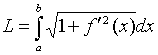 . (28)
. (28)
3.2.
Если кривая задана параметрическими
уравнениями 
![]() ,
где x(t), y(t) дифференцируемые
функции, то длина дуги
,
где x(t), y(t) дифференцируемые
функции, то длина дуги
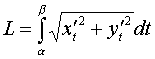 . (29)
. (29)
3.3. Если дуга задана в полярных координатах , , то длина дуги
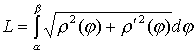 . (30)
. (30)
П р и м е р 20. Вычислить длины дуг плоских кривых:
а) ![]() ; б)
; б) 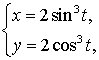
![]() ;
;
в) ![]() ,
, ![]() .
.
Решение.
а) Воспользуемся формулой (10). Так как ![]()
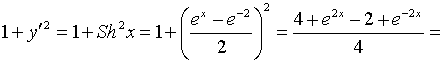
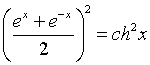 ,
,
то
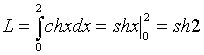 .
.
б)
Воспользуемся формулой (11). Так как ![]()
![]()
![]() ,
то
,
то .
.
в)  .
.
4. Вычисление объемов. Нахождение объемов некоторых тел можно свести к вычислению определенных интегралов.
4.1.
Вычисление объема тела по известным
площадям параллельных сечений. Если
известны площади сечений тела плоскостями,
перпендикулярными оси OX,
т. е., зная х, мы
можем вычислить площадь сечения S = S (x).
Тогда объем тела 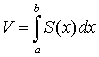 в
предположении, что S(x) интегрируемая
функция.
в
предположении, что S(x) интегрируемая
функция.
4.2. Вычисление объема тела вращения:
а)
если тело образовано вращением
криволинейной трапеции, ограниченной
кривой y = f(x),
осью OX и
двумя прямыми x = a и x = b(a < b)
вокруг оси OX,
то объем тела 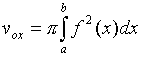 ;
;
б)
а если тело образовано вращением фигуры,
ограниченной кривой ![]() ,
прямыми y=c, y=d (c<d) и
осью OY,
вокруг оси OY,
то его объем
,
прямыми y=c, y=d (c<d) и
осью OY,
вокруг оси OY,
то его объем  ;
;
в)
если тело образовано вращением вокруг
оси OY фигуры,
ограниченной линией y = f (x), прямыми x = a, x = b ![]() и
осью OX,
то его объем можно вычислить по формуле
и
осью OX,
то его объем можно вычислить по формуле 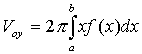 ;
;
г)
если вращается вокруг полярной оси
криволинейный сектор, ограниченный
дугой ![]() ,
двумя полярными радиусами
,
двумя полярными радиусами ![]() и
и ![]() ,
то объем полученного тела может
быть вычислен по формуле
,
то объем полученного тела может
быть вычислен по формуле 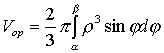 .
.
П
р и м е р 21. Вычислить объем тела,
образованного вращением фигуры,
ограниченной графиками функций ![]() и
и ![]() вокруг
оси OX.
вокруг
оси OX.
Решение. Найдем точки пересечения параболы и прямой . Решим систему:
![]()
![]()
![]()
Получим две точки пересечения:
х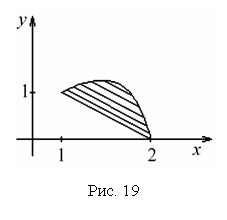 1 =
1, у1 =
1; х2 =
2, у2 =
0.
1 =
1, у1 =
1; х2 =
2, у2 =
0.
Сделаем чертеж (рис. 19).

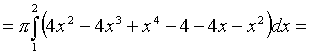

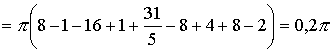 .
.
Рис. 20
|
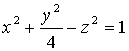 ; z = 0; z = 3.
; z = 0; z = 3.
Решение. ![]() однополостной
гиперболоид. При
пересечении его плоскостями z = h в
сечении получаем эллип-сы
однополостной
гиперболоид. При
пересечении его плоскостями z = h в
сечении получаем эллип-сы ![]() (рис.
20) с полуосями
(рис.
20) с полуосями ![]() ,
, ![]() .
Как известно, площадь эллипса
.
Как известно, площадь эллипса ![]()
![]()
![]()
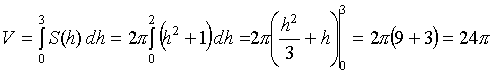 куб.
ед.
куб.
ед.
5. Вычисление площади поверхности вращения
5.1. Поверхность, образованная вращением кривой , a < x < b вокруг оси OX, имеет площадь
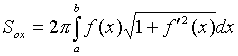 .
.
5.2. Если кривая задана параметрическими уравнениями
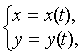
![]() ,
,
причем ![]() ,
то
,
то
![]() .
.
5.3.
Если дуга ![]() ,
, ![]() ,
задана в полярной системе координат
кривой, и вращается вокруг полярной
оси, то площадь поверхности вращения
можно вычислить по формуле
,
задана в полярной системе координат
кривой, и вращается вокруг полярной
оси, то площадь поверхности вращения
можно вычислить по формуле
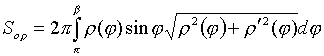
 .
.
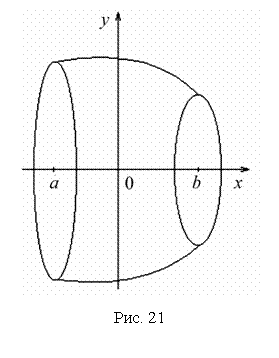
П
р и м е р 23. Найти площадь поверхности
шарового пояса, образованного вращением
части окружности x2 + y2 = R2 ![]() вокруг
оси OX (рис.
21).
вокруг
оси OX (рис.
21).
Решение.
Из уравнения окружности имеем ![]() .
Вращаем вокруг оси ОХ дугу
верхней части.
.
Вращаем вокруг оси ОХ дугу
верхней части.
Найдем 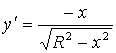 и
и 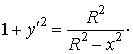 Тогда
по соответствующей формуле площадь
шарового пояса
Тогда
по соответствующей формуле площадь
шарового пояса
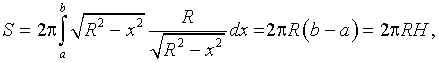
![]()
Физические приложения определенного интеграла
Вычисление работы с помощью определённого интеграла.
Пусть
под действием некоторой силы ![]() материальная
точка М движется по прямой в направлении
оси
материальная
точка М движется по прямой в направлении
оси ![]() .
Требуется найти работу, произведённую
силой
при
перемещении точки М из положения
.
Требуется найти работу, произведённую
силой
при
перемещении точки М из положения ![]() в
положение
в
положение ![]() .
.
1) Если
сила постоянна ![]() ,
то работа выражается следующим образом
,
то работа выражается следующим образом ![]() .
.
2) Если
сила переменная величина, то 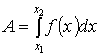 .
.
Пример:
Два
электрических заряда ![]() и
и ![]() находятся
на оси
соответственно
в точках
находятся
на оси
соответственно
в точках ![]() и
и ![]() .
Какая работа будет произведена, если
второй заряд переместится в точку
.
Какая работа будет произведена, если
второй заряд переместится в точку ![]() ?
(Сила взаимодействия зарядов
?
(Сила взаимодействия зарядов ![]() ).
).
Решение:
= =
=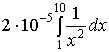 =
=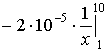 =
=
=![]() .
.
Координаты центра тяжести.
Центром тяжести совокупности материальных точек называется центр параллельных сил тяжести, приложенных в этих точках.
Для
материальной дуги АВ плоской
кривой ![]() прямоугольные
координаты центра тяжести
прямоугольные
координаты центра тяжести ![]() определяются
формулами
определяются
формулами ![]() :
:
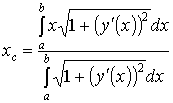 ,
, 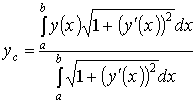 .
.
Для
материальной однородной криволинейной
трапеции, прилежащей к оси
и
имеющей верхнюю границу ![]() ,
центр тяжести имеет координаты
,
центр тяжести имеет координаты
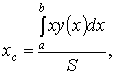
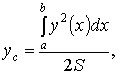
где ![]() площадь
криволинейной трапеции.
площадь
криволинейной трапеции.
Центр тяжести произвольной плоской, ограниченной графиком функции
![]()
![]() сверху
и
сверху
и ![]() снизу,
определяется формулами
снизу,
определяется формулами

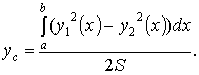
Пример:
Найти
координаты центра тяжести однородного
полукруга ![]() ,
расположенного над осью
.
,
расположенного над осью
.
Решение:
Применим формулы

Так
как полукруг расположен над осью
,
то верхняя граница задаётся уравнением ![]() В
силу симметрии фигуры относительно оси
ординат, абсцисса
В
силу симметрии фигуры относительно оси
ординат, абсцисса ![]() центра
тяжести равна нулю. Найдём ординату:
центра
тяжести равна нулю. Найдём ординату:
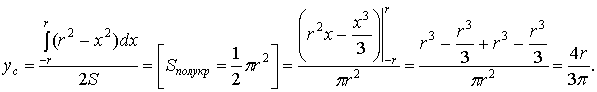
Координаты
центра тяжести имеют вид 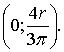
32.Вопрос.Понятие функции нескольких переменных
(Определение, область определения, область значений, график, линии уровня).Примеры
Функции нескольких переменных |
|
1. Функция двух переменных и ее область определения |
Определение. Переменная 1) задано
множество 2) задан
закон, по которому каждой паре чисел При этом переменные и называются аргументами или независимыми переменными. Обозначения функций двух переменных аналогичны обозначениям функций одной переменной:
При
нахождении частного значения Определение. Множество всех пар значений аргументов данной функции двух переменных называется областью определения этой функции. Например,
областью определения функции Графиком функции двух переменных в прямоугольной декартовой системе координат в пространстве является в общем случае поверхность. Линией
уровня функции
называется
линия Аналогично |
Определение. Пусть имеется п переменных величин, и каждому набору их значений (хх, х2,..., хп) из некоторого множества X соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана функция нескольких переменныхz=f(хх, х2,..., хп).
Переменные хх, х2,..., хп называются независимыми переменными или аргументами, z — зависимой переменной, а символ f означает закон соответствия. Множество Xназывается областью определения функции. Очевидно, это подмножество n-мерного пространства.

Функцию двух переменных обозначают z=f(x, у). Тогда ее область определения X есть подмножество координатной плоскости Оху.
Окрестностью
точки ![]() называется
круг, содержащий точку
называется
круг, содержащий точку ![]() (см.
рис. 1).
(см.
рис. 1).
Очевидно, круг на плоскости есть двумерный аналог интервала на прямой.
При
изучении функций нескольких переменных
используется математический аппарат:
любой функции z=f(x,
у) можно
поставить в соответствие пару функций
одной переменной: при фиксированном
значении х=х0 функцию z= ![]() и
при фиксированном значении у=у0 функцию z=f(x,
у0).
и
при фиксированном значении у=у0 функцию z=f(x,
у0).
Графиком функции двух переменных z= называется множество точек трехмерного пространства (х, у, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением z= .
Для построения графика функции z=f(x, у) полезно рассматривать функции одной переменной z=f(x, у0) и z= , представляющие сечения графика z=f(x, у)плоскостями, параллельными координатным плоскостям Oxz и Oyz, т.е. плоскостями у= у0 и х=х0.

Пример
1. Построить график функции ![]() .
.
Решение.
Сечения поверхности
= ![]() плоскостями,
параллельными координатным
плоскостям Oyz и Oxz,
представляют параболы (например,
при х
= 0
плоскостями,
параллельными координатным
плоскостям Oyz и Oxz,
представляют параболы (например,
при х
= 0 ![]() ,
при у = 1
,
при у = 1 ![]() и
т.д.). В сечении поверхности кординатной
плоскостью Оху,
т.е. плоскостью z=0,
получается окружность
и
т.д.). В сечении поверхности кординатной
плоскостью Оху,
т.е. плоскостью z=0,
получается окружность ![]() График
функции представляет поверхность,
называемую параболоидом (см. рис. 2)
График
функции представляет поверхность,
называемую параболоидом (см. рис. 2)
Определение. Линией уровня функции двух переменных z=f{x, у) называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно С. Число С в этом случае называется уровнем.

На
рис.3 изображены линии уровня,
соответствующие значениям С=1 и С=2.
Как видно, линия уровня ![]() состоит
из двух непересекающихся кривых.
Линия
состоит
из двух непересекающихся кривых.
Линия ![]() –
самопересекающаяся кривая.
–
самопересекающаяся кривая.
Многие примеры линий уровня хорошо известны и привычны. Например, параллели и меридианы на глобусе — это линии уровня функций широты и долготы. Синоптики публикуют карты с изображением изотерм — линий уровня температуры.

Пример 2. Построить линии уровня функции .
Решение.
Линия уровня z=C это
кривая на плоскости Оху, задаваемая
уравнением х2+ у2 -
2у
= С или х2 +
(у - I)2 =
С+1. Это уравнение окружности с центром
в точке (0; 1) и радиусом ![]() (рис.
4).
(рис.
4).
Точка (0; 1) — это вырожденная линия уровня, соответствующая минимальному значению функции z=-1 и достигающемуся в точке (0; 1). Линии уровня — концентрические окружности, радиус которых увеличивается с ростом z=C, причем расстояния между линиями с одинаковым шагом уровня уменьшаются по мере удаления от центра. Линии уровня позволяют представить график данной функции, который был ранее построен на рис. 2.
Частные производные
Дадим
аргументу х приращение ∆х, аргументу у
— приращение ∆у. Тогда
функция zполучит
наращенное значение f(х+∆х,
у+∆у). Величина ∆z=f(x+∆x,
y+∆y)-f{x, у)называется полным
приращением функции в
точке (х;
у). Если
задать только приращение аргумента x или
только приращение аргумента у, то
полученные приращения функции
соответственно ![]() и
и ![]() называются частными.
называются частными.
Полное
приращение функции, вообще говоря, не
равно сумме частных, т.е. ![]()
Пример 15.6.Найти частные и полное приращения функции z=xy.
Решение. ![]() ;
;
;
; ![]() .
.
Получили, что
Определение. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует).
Обозначается
частная производная так: ![]() или
или ![]() ,
или
,
или ![]() .
.
Для
нахождения производной ![]() надо
считать постоянной переменную у, а для
нахождения
надо
считать постоянной переменную у, а для
нахождения ![]() — переменную
х. При
этом сохраняются известные правила
дифференцирования.
— переменную
х. При
этом сохраняются известные правила
дифференцирования.
Пример.Найти частные производные функции:
a) z=x ln y+ ![]() .
.
Решение:
Чтобы найти частную производную
по х, считаем у постоянной
величиной. Таким образом, ![]() . Аналогично,
дифференцируя по у,считаем х постоянной
величиной, т.е
. Аналогично,
дифференцируя по у,считаем х постоянной
величиной, т.е ![]() .
.
Дифференциал функции
Определение. Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.
dz= ![]() . (1)
. (1)
Учитывая,
что для функций f(х, у)=х,
g(x, у)=у согласно
(1) df=dx=∆x;
dg=dy=∆yформулу
дифференциала (1) можно записать в
виде dz=z'x dx+z'y dy (2)или ![]()
Определение.Функция
z=f(x, у) называется дифференцируемойв
точке (х, у), если ее полное приращение
может быть представлено в виде ![]() (3),где
dz — дифференциал
функции,
(3),где
dz — дифференциал
функции, ![]() –
,бесконечно малые при
–
,бесконечно малые при ![]() .
.
Достаточное условие дифференцируемости функции двух переменных.
Теорема.Если частные производные функции z'v (x, у) существуют в окрестности точки (х, у) и непрерывны в самой точке (х, у), то функция z=f{x, у) дифференцируема в этой точке.
33.Вопрос.Частные приращения и частные производные функции нескольких переменных. Примеры. Геометрический смысл частных производных функций двух переменных.
ЧАСТНЫЕ ПРИРАЩЕНИЯ И ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ


 сходится,
поскольку существует конечный предел
соответствующего определенного
интеграла:
сходится,
поскольку существует конечный предел
соответствующего определенного
интеграла:
 сходится,
поскольку существует конечный предел
соответствующего определенного
интеграла при
сходится,
поскольку существует конечный предел
соответствующего определенного
интеграла при 

 расходится,
поскольку предел соответствующего
определенного интеграла не существует:
расходится,
поскольку предел соответствующего
определенного интеграла не существует:

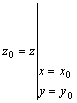 или
или