1 Вопрос. Производная функции одной переменной

Определение: геометрический и механический смысл

Примеры нахождения производных по определению.

Пример 1

Вычислить производную функции   в точке 

Справка: Следующие способы обозначения функции эквивалентны: В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».

Сначала находим производную:

Надеюсь, многие уже приноровились находить такие производные устно.

На втором шаге вычислим значение производной в точке  :

Готово.

Небольшой разминочный пример для самостоятельного решения:

Пример 2

Вычислить производную функции   в точке 

Пример 2: Найдем производную:

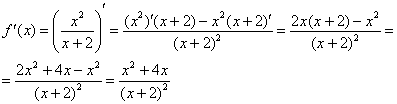
Геометрический и механический смысл производной

С вычислением производной мы сталкиваемся всякий раз, когда требуется определить скорость изменения одной величины - функции в зависимости от изменения другой величины - независимой переменной.

Определение

Средней скоростью изменения функции   при переходе независимой переменной от значения   к значению   называется отношение приращения   функции к приращению   независимой переменной, то есть

Определение

Истинной или мгновенной скоростью изменения функции   при заданном значении независимой переменной   называется предел, к которому стремится средняя скорость изменения функции при стремлению к нулю приращения аргумента  :

Механический смысл производной

Теорема

(Механический смысл производной)

Пусть задан путь   движения материальной точки. Скорость данной материальной точки в момент времени   есть производная от пути   по времени  :

Пример

Задание. Тело движется прямолинейно по закону   (м). Определить скорость его движения в момент   с.

Решение. Искомая скорость - это производная от пути, то есть

В заданный момент времени

 (м/с).

Ответ.   (м/с).

Геометрический смысл производной

Производная функции  , вычисленная при заданном значении  , равна тангенсу угла, образованного положительным направлением оси   и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой  :

Замечание

Геометрически производная представляет собой угловой коэффициент касательной к графику функции  в точке   .

Пример

Задание. На рисунке №1 изображен график функции   и касательная к нему в точке с абсциссой   . Найти значение  .

Решение. Из геометрического смысла производной получаем, что

Найдем угол  . Рассмотрим треугольник   - прямоугольный, равнобедренный. Тогда , а значит

А отсюда следует, что

Ответ. 

2 Вопрос. Уравнения касательной и нормали к кривой

Касательная и нормаль к кривой

Определение

Касательная прямая - прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Определение

Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.

Если кривая определена уравнением  , то уравнение касательной к ней в точке   имеет вид:

а уравнение нормали:

Пример

Задание. Написать уравнение касательной и нормали к кривой   в точке с абсциссой .

Решение. Находим значение функции в заданной точке:

Далее вычислим значение производной функции в точке  :

а тогда уравнение касательной запишется в виде:

или после упрощения:

уравнение нормали:

Ответ. Уравнение касательной: 

Уравнение нормали: 

Составить уравнения касательной и нормали к графику функции   в точке с абсциссою
Решение.	Определим ординату точки, имеющей абсциссу  . Подставляя это значение в функцию, получим: Далее найдем производную заданной функции и вычислим её значение в точке  Пользуясь формулой составим уравнение касательной Используя формулу составим уравнение нормали
Ответ.	Уравнение касательной:  Уравнение нормали:

3. Вопрос.Cвязь между непрерывностью и дифференцируемостью. Правила дифференцирования.

Теорема о непрерывности дифференцируемой функции

		Теорема. Если функция    дифференцируема в некоторой точке  a, то она непрерывна в этой точке.  Доказательство. По определению производной Это предельное равенство означает, что выражение под знаком предела можно представить в виде где  α(x)  – бесконечно малая функция при  x → a. Тогда Следовательно,     при  x → a.  Заметим, что дифференцируемость функции в некоторой точке означает ее гладкость в окрестности этой точки, что влечет за собой непрерывность функции в рассматриваемой точке. Однако обратное утверждение несправедливо – функция, обладающая свойством непрерывности в некоторой точке, не обязательно дифференцируема в этой точке.   Рис. 8. Непрерывная в точке a функция     не является дифференцируемой в этой точке.

К основным правилам дифференцирования относят:

Вынесение постоянного множителя за знак производной.

Докажем формулу  . По определению производной имеем:

Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому

На этом доказательство первого правила дифференцирования завершено.

Пример.

Найти производную функции  .

Решение.

Из таблицы производных для тригонометрических функций видим  . Воспользуемся правилом вынесения множителя за знак производной:

Достаточно часто приходится сначала упрощать вид дифференцируемой функции, чтобы воспользоваться таблицей производных и правилами нахождения производных. Следующие примеры это наглядно подтверждают.

Пример.

Выполнить дифференцирование функции  .

Решение.

По свойствам логарифмической функции можно перейти к записи  . Осталось вспомнить производную логарифмической функции и вынести постоянный множитель:

Пример.

Найти производную функции  .

Решение.

Преобразуем исходную функцию  .

Применяем правило вынесения множителя за знак производной и из таблицы берем производную показательной функции:

Производная суммы, производная разности.

Для доказательства второго правила дифференцирования  воспользуемся определением производной и свойством предела непрерывной функции.

Подобным образом можно доказать, что производная суммы (разности) n функций равна сумме (разности) n производных  .

Пример.

Найти производную функции  .

Решение.

Упростим вид исходной функции  .

Используем правило производной суммы (разности): 

В предыдущем пункте мы доказали, что постоянный множитель можно выносить за знак производной, поэтому

Осталось воспользоваться таблицей производных:

К началу страницы

Производная произведения функций.

Докажем правило дифференцирования произведения двух функций  .

Запишем предел отношения приращения произведения функций к приращению аргумента. Будем учитывать, что   и   (приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).

Что и требовалось доказать.

Пример.

Продифференцировать функцию  .

Решение.

В данном примере  . Применяем правило производной произведения:

Обращаемся к таблице производных основных элементарных функций и получаем ответ:

Пример.

Найти производную функции  .

Решение.

В этом примере  . Следовательно,

Давайте рассмотрим случай нахождения производной произведения трех функций. В принципе, по этой же системе можно дифференцировать произведение и четырех, и пяти, и двадцати пяти функций.

Пример.

Выполнить дифференцирование функции  .

Решение.

Будем исходить из правила дифференцирования произведения двух функций. В качестве функции f(x) будем считать произведение (1+x)sinx, а в качестве g(x) возьмем lnx:

Для нахождения   вновь применяем правило производной произведения:

Используем правило производной суммы и таблицу производных:

Подставляем полученный результат:

Как видите, порой приходится применять несколько правил дифференцирования в одном примере. Сложного в этом ничего нет, главное действовать последовательно и не мешать все в кучу.

Пример.

Найти производную функции  .

Решение.

Функция представляет собой разность выражений   и  , поэтому

В первом выражении выносим двойку за знак производной, а ко второму выражению применяем правило дифференцирования произведения:

Производная произведения функций.

Докажем правило дифференцирования произведения двух функций  .

Запишем предел отношения приращения произведения функций к приращению аргумента. Будем учитывать, что   и   (приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).

Что и требовалось доказать.

Пример.

Продифференцировать функцию  .

Решение.

В данном примере  . Применяем правило производной произведения:

Обращаемся к таблице производных основных элементарных функций и получаем ответ:

Пример.

Найти производную функции  .

Решение.

В этом примере  . Следовательно,

Давайте рассмотрим случай нахождения производной произведения трех функций. В принципе, по этой же системе можно дифференцировать произведение и четырех, и пяти, и двадцати пяти функций.

Пример.

Выполнить дифференцирование функции  .

Решение.

Будем исходить из правила дифференцирования произведения двух функций. В качестве функции f(x) будем считать произведение (1+x)sinx, а в качестве g(x) возьмем lnx:

Для нахождения   вновь применяем правило производной произведения:

Используем правило производной суммы и таблицу производных:

Подставляем полученный результат:

Как видите, порой приходится применять несколько правил дифференцирования в одном примере. Сложного в этом ничего нет, главное действовать последовательно и не мешать все в кучу.

Пример.

Найти производную функции  .

Решение.

Функция представляет собой разность выражений   и  , поэтому

В первом выражении выносим двойку за знак производной, а ко второму выражению применяем правило дифференцирования произведения:

Производная частного двух функций (производная дроби).

Докажем правило дифференцирования частного двух функций (дроби)  . Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X.

По определению производной

Пример.

Выполнить дифференцирование функции  .

Решение.

Исходная функция представляет собой отношение двух выражений sinx и 2x+1. Применим правило дифференцирования дроби:

Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной:

В заключении, давайте соберем все правила в одном примере.

Пример.

Найти производную функции  , где a – положительное действительное число.

Решение.

А теперь по порядку.

Первое слагаемое  .

Второе слагаемое

Третье слагаемое

Собираем все вместе:

4.Вопрос.Производные Основных элементарных функций.

Задание. Найти производную функции 

Решение. Используем правила дифференцирования и таблицу производных:

Ответ. 

5.Вопрос.Производная сложной функции примеры

Все примеры этого раздела опираются на таблицу производных и теорему о производной сложной функции, формулировка которой такова:

Пусть 1) функция u=φ(x) имеет в некоторой точке x0 производную u′x=φ′(x0), 2) функция y=f(u) имеет в соответствующей точке u0=φ(x0) производную y′u=f′(u). Тогда сложная функция y=f(φ(x)) в упомянутой точке также будет иметь производную, равную произведению производных функций f(u) и φ(x):

(f(φ(x)))′=f′u(φ(x0))⋅φ′(x0)

или, в более короткой записи: y′x=y′u⋅u′x.

В примерах этого раздела все функции имеют вид y=f(x) (т.е. рассматриваем лишь функции одной переменной x). Соответственно, во всех примерах производная y′ берётся по переменной x. Чтобы подчеркнуть то, что производная берётся по переменной x, часто вместо y′ пишут y′x.

В примерах №1, №2 и №3 изложен подробный процесс нахождения производной сложных функций. Пример №4 предназначен для более полного понимания таблицы производных и с ним имеет смысл ознакомиться.

Желательно после изучения материала в примерах №1-3 перейти к самостоятельному решению примеров №5, №6 и №7. Примеры №5, №6 и №7 содержат краткое решение, чтобы читатель мог проверить правильность своего результата.

Пример №1

Найти производную функции y=ecosx.

Решение

Нам нужно найти производную сложной функции y′. Так как y=ecosx, то y′=(ecosx)′. Чтобы найти производную (ecosx)′ используем формулу №6 из таблицы производных. Дабы использовать формулу №6 нужно учесть, что в нашем случае u=cosx. Дальнейшее решение состоит в банальной подстановке в формулу №6 выражения cosx вместо u:

Итак,

y′=(ecosx)′=ecosx⋅(cosx)′(1.1)

Теперь нужно найти значение выражения (cosx)′. Вновь обращаемся к таблице производных, выбирая из неё формулу №10. Подставляя u=x в формулу №10, имеем: (cosx)′=−sinx⋅x′. Теперь продолжим равенство (1.1), дополнив его найденным результатом:

y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)(1.2)

Так как x′=1, то продолжим равенство (1.2):

y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)=ecosx⋅(−sinx⋅1)=−sinx⋅ecosx(1.3)

Итак, из равенства (1.3) имеем: y′=−sinx⋅ecosx. Естественно, что пояснения и промежуточные равенства обычно пропускают, записывая нахождение производной в одну строку, – как в равенстве (1.3). Итак, производная сложной функции найдена, осталось лишь записать ответ.

Ответ: y′=−sinx⋅ecosx.

Пример №2

Найти производную функции y=9⋅arctg12(4⋅lnx).

Решение

Нам необходимо вычислить производную y′=(9⋅arctg12(4⋅lnx))′. Для начала отметим, что константу (т.е. число 9) можно вынести за знак производной:

y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′(2.1)

Теперь обратимся к выражению (arctg12(4⋅lnx))′. Чтобы выбрать нужную формулу из таблицы производных было легче, я представлю рассматриваемое выражение в таком виде: ((arctg(4⋅lnx))12)′. Теперь видно, что необходимо использовать формулу №2, т.е. (uα)′=α⋅uα−1⋅u′. В эту формулу подставим u=arctg(4⋅lnx) и α=12:

Дополняя равенство (2.1) полученным результатом, имеем:

y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′(2.2)

Примечание: показать\скрыть

Теперь нужно найти (arctg(4⋅lnx))′. Используем формулу №19 таблицы производных, подставив в неё u=4⋅lnx:

(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′

Немного упростим полученное выражение, учитывая (4⋅lnx)2=42⋅(lnx)2=16⋅ln2x.

(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′=11+16⋅ln2x⋅(4⋅lnx)′

Равенство (2.2) теперь станет таким:

y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′(2.3)

Осталось найти (4⋅lnx)′. Вынесем константу (т.е. 4) за знак производной: (4⋅lnx)′=4⋅(lnx)′. Для того, чтобы найти (lnx)′ используем формулу №8, подставив в нее u=x: (lnx)′=1x⋅x′. Так как x′=1, то (lnx)′=1x⋅x′=1x⋅1=1x. Подставив полученный результат в формулу (2.3), получим:

y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′==108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅4⋅1x=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).

Напомню, что производная сложной функции чаще всего находится в одну строку, – как записано в последнем равенстве. Поэтому при оформлении типовых расчетов или контрольных работ вовсе не обязательно расписывать решение столь же подробно.

Ответ: y′=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).