КР (вариант 5)

Контрольная «Управление в БТС»

Группа 7501 Фамилия Исаков А.О.

ВОПРОС 5. Задача ЛП с ограничениями-неравенствами. Переход от нее к основной задаче.

Пусть заданы условия:

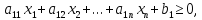
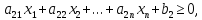
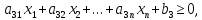
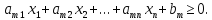
5.1. Преобразуйте неравенства в уравнения-ограничения.

5.2. Определите набор свободных и базисных переменных.

5.3. Укажите, при каких условиях задача решается геометрическим способом, а при каком вычислительным. В каком случае не требуется применения ЛП?

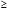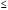5.4. Что изменится, если в третьем неравенстве вместо знака будет . Пути решения такой изменённой задачи.

5.1. Преобразуйте неравенства в уравнения-ограничения

Пусть имеется задача ЛП с параметрами

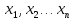
Ограничения имеют вид неравенств

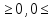
Методом перестановки приводим к

Тогда ограничения могут принять такой вид:

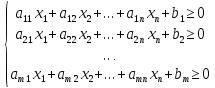
Обозначим эту систему неравенств как (*)

Требуется найти такие неотрицательные значения 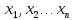, которые удовлетворяют системе неравенств и обращают в минимум линейную функцию L.

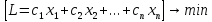
Используется следующий прием:

Вводятся следующие переменные

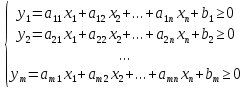
Обозначим эту систему уравнений как (**)

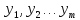– добавочные переменные. Они также, как и исходные, должны быть неотрицательными .

Тогда возникает новая ЗЛП в следующей постановке:

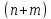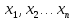
Найти такие неотрицательные значения переменных 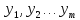, чтобы они удовлетворяли системе линейных неравенств (**) и, кроме того, обращали бы функцию .

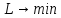5.2. Определите набор свободных и базисных переменных.

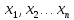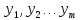В такой подстановке – рассматриваются как свободные переменные. А переменные – рассматриваются как базисные.

Перешли к классической подстановке.

5.3. Укажите, при каких условиях задача решается геометрическим способом, а при каком вычислительным. В каком случае не требуется применения ЛП?

Отличие:

• Функция L сразу выражена через свободные переменные.

• Если их только 2, то используют геометрический метод (n-m=2, m – число уравнений, n – число переменных).

• Если их больше 2-х, то используют вычислительные методы (n-m>2).

Если 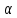– линейные ограничения на элементы решения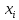, то чаще используют методы линейного программирования. Если исследуется динамика некоторой системы, т.е. развитие ее состояния во времени и удается выделить некоторые промежуточные состояния системы, то используют методы динамического программирования.

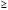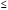5.4. Что изменится, если в третьем неравенстве вместо знака будет . Пути решения такой изменённой задачи.

Пусть имеется задача ЛП с n переменными 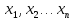, в которой ограничения, наложенные на эти переменные, имеют вид линейных неравенств. В некоторых из них знак неравенства может быть ≥, в других ≤. Второй вид сводится к первому переменой знака в обеих частях неравенства. Поэтому задаем все ограничения в стандартной форме.

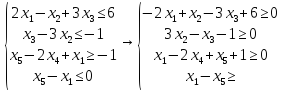
После введения дополнительных переменных:

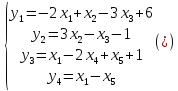
Задача сводится к тому, чтобы найти неотрицательные значения переменных 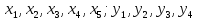удовлетворяющие уравнениям (*) и обращающие в минимум линейную функцию .

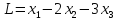Мы показали, как от задачи ЛП с ограничениями-неравенствами можно перейти к задаче с ограничениями-равенствами (ОЗЛП).

Пример

Заданы 3 уравнения:

Требуется:

1. Записать эту задачу как задачу ограничения неравенств

2. Решить основную задачу

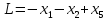
Решение:

n=5 (кол-во переменных)

m=3 (кол-во уравнений)

n-m=2=k

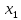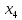Пусть и свободные переменные

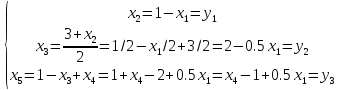
Осуществили обратный переход

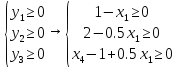
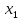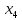и свободные

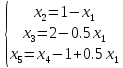
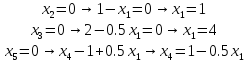
Штриховка так, чтобы

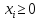
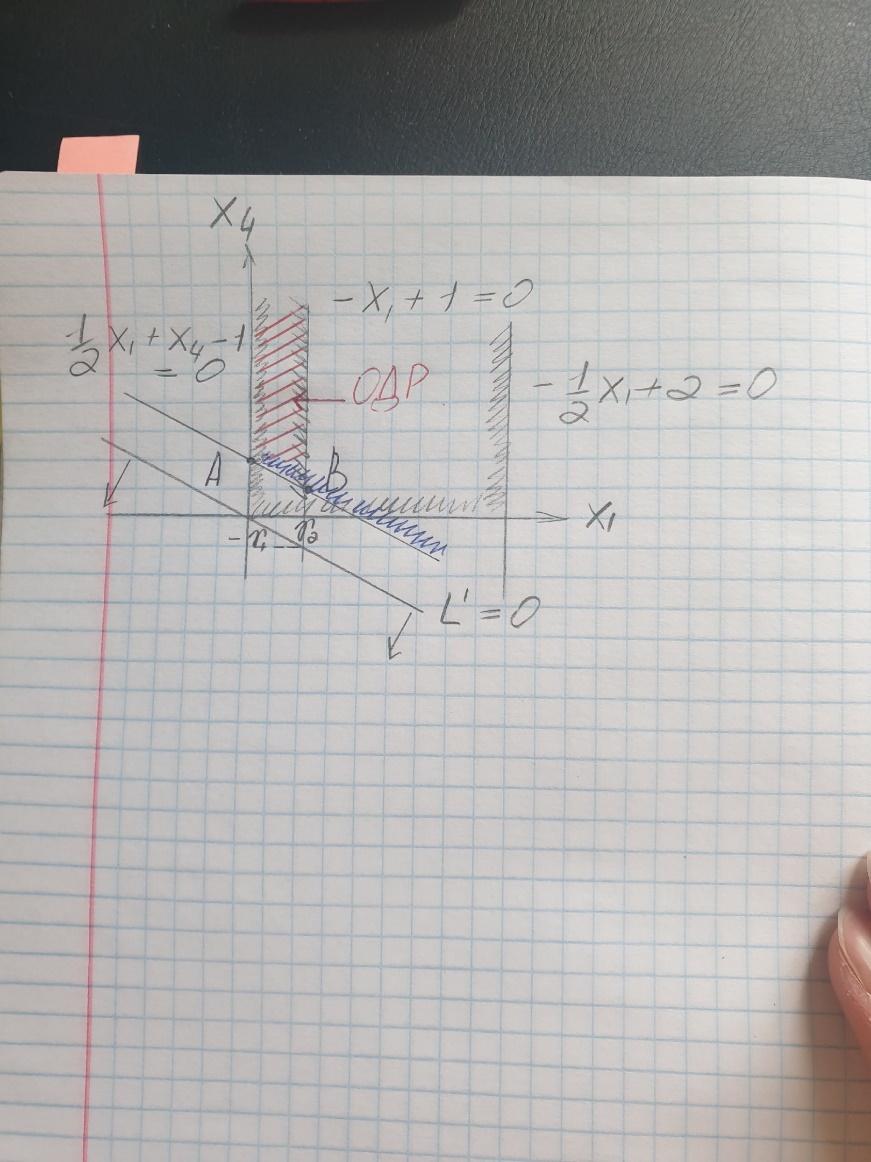
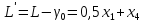
Получили открытую ОДР, следовательно, решение на [AB]

(если бы по условию , то решения не было бы)

Решение в опорной точке (.)А:

4