9.Расчет необходимой и достаточной точности( принцип «равных влияний»).

В практике часто приходится решать задачу: задана определенная точность результата. Требуется определить с какой точностью должны быть получены результаты измерений, чтобы заданная точность была достигнута.Эта задача решается по формуле: 

,но величину (m) следует считать известной, а величины m1; m2; mn подлежат определению. При n > 1 задача неопределенна, то есть допускает бесчисленное число решений. Из которых можно выбрать наиболее выгодное, в частности пользуясь принципом равных влияний, то есть допускается, что ошибки m1; m2; mn одинаково влияют на величину m.

.Написанное выражение определяет m1; m2; mn с точностью, с которой надо измерять х1, х2, хn.

10.Определение средней квадратической ошибки одного измерения по разностям двойных равноточных измерений( без учета и с учетом систематических ошибок).

Если каждая величина измерена 2 раза и все измерения равноточны(измерения превышения по черной и красной сторонам рейки), то сред.квад.ошибка одного измерения можно определить по разностям полученным для каждой пары измерений след. образом: = - , = - , = -

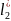Если бы все измерения были без ошибки,то разности были бы равны 0,следовательно, разность двойных измерений можно рассматривать как истинные ошибки: = ,но ,где и - сред.квад.ошибка. = m. =m .подставляю в (1)m=

Эта формула дает выражение для сред.квад.ошибки отдельного измерения при отсутствии систематических ошибок, если разности двойных измерений содержат постоянную ошибку, то ее предварительно необходимо исключить, если d1,d2,…dnистинные погрешности,то их сумма при значительном их кол-ве будет суммой постоянных ошибок разности измерений, и тогда: = . Случайную часть ошибок разности двойных измерений: =d1-d0 , =d2-d0, 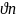=dn-d0 ,получаем = в связи с преобразованиями получаем: m= -

11.Неравноточные измерения. Веса измерений и их свойства.

Для определения наиболее надежного значения из ряда неравноточных измерений и оценим их точности вводят, так называемые веса измерений, которые показывают степень надежности (доверия), выполненных измерений. Вес измерений определяют :P=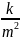 - вес измерения, где k-произвольное число ,которое должно быть одним и тем же при определении весов всех измерений, участвующих в решении какой либо задачи.

m-квадрат средней квадратической погрешности. Из определения веса следует, что чес более точно произведенно измерения ,тем больше его вес и наоборот. Т.к. k-произвольное число, то все веса участвующие при решении задачи можно увеличить и уменьшить в одно и тоже число раз. Это свойство весов показывает, что веса не абсолютные, а относительные. По ним можно судить только о том, во сколько раз одно измерение точнее другого. , т.е. веса двух измерений обратно пропорциональны квадрату их сред.квад.ошибки практически смысл ведения весов заключ. в том ,что веса в отличие от сред.квад.ошиб.в ряде случаев могут быть определены заранее.

12.Весовое среднее. Средняя квадратическая ошибка единицы веса и средняя квадратическая ошибка весового среднего.

Средние квадратические ошибки неравноточных измерений различны, поэтому для оценки точности таких измерений выбирают общую меру. Такой мерой является средняя квадратическая ошибка такого измерения, вес которого равен единице.Следует отметить, что величина М (средняя квадратическая ошибка веса) может относится к воображаемому измерению, если среди результатов нет ни одного с весом равным единице. .Установим связь между средней квадратической ошибкой единицы веса М и средней квадратической ошибкой результата измерений с весом :

. Если имеем ряд неравноточных измерений с весами P1, P2, P3 и средней квадратической ошибкой m1, m2,...,mn, то для каждого результата измерений ошибки веса будут равны:

.Среднее квадратическое значение из этого ряда будет: . Если заменить m на ∆ или δ, то получим соответственно:

. Эту формулу можно применять для связи ошибки весового среднего М0 с весом [P] и ошибкой единицы веса М, то есть можно записать: