1.Сущность и виды геодезических измерений. Ошибки измерений и их классификация.

а)Измерения играют весьма важную роль во всех областях науки и техники; они дают количественную информацию об объектах и явлениях, происходящих в природе, позволяют устанавливать происходящие в ней закономерности. Различают непосредственные и косвенные измерения.  При непосредственных измерениях выполняют непосредственное сравнение определяемой величины с единицей меры. Примером может слу­жить изменив длины путем последовательного укладывания мерного прибора (мерной ленты, рулетки) вдоль измеряемой линии. При косвенных измерениях определяемую величину находят путем вычислений по результатам непосредственных измерении одной или нескольких величин, связанных с определяемой величиной математической зависимостью. Примерами являются определения длин линии оптиче­скими дальномерами, параллактическим способом, светодальномерами и радиодальномерами.

б) Под погрешностью измерения величиныпонимают отклонение результата измерения от его истинного (действительного) значения, т. е.

А = 1-Х (1),где А — истинная погрешность измерения; / — результат измерения; X — истинное значение величины. Погрешности измерений можно классифицировать по двум призна­кам: по источнику происхождения; по характеру их действия на резуль­таты измерений и свойствам.

По источнику происхождения различают погрешности средства измерения (приборные), личные (субъективные), внешние и метода из­мерений.  По характеру действия погрешностей на результаты измерений их разделяют на грубые, систематические и случайные.

2.Свойство случайных ошибок измерений.

а) Свойство ограниченности- по абсолютной величине погрешности не превосходят некоторого предела.

б) Свойство симметричности- положительные и отрицательные погрешности, равные по асолютной величине, встречаются в ряду измерений одинаково часто.

в)Свойство унимодальности – малые по абсолютной величине погрешности должны встречаться чаще, чем большие.

г) Свойство компенсации – при неограниченном числе измерений предел среднего значения погрешностей стремится к нулю .

3.Арифмитическая середина.

Пусть какая-нибудь величина была измерена n раз и получили следующие равноточные измерения , ,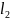… . Если х-точное значение измеренное величины, то можно составить ряд равенств: -x= , -x= ,…., -x= .

Складывая левые и правые части этих равенств получим:

+ +…+ -nx= + +…+ или х= -

Т.еn→∞ ,тогда и т.е предел ср.ариф. при n→∞ ,стремится к истинному значению велечины = 0 . На основании (1) можно утверждать, что из одинаковых точных измерений явл. наиболее надежным результатом при любом числе измерений, если n>1.

4. Средняя квадратическая ошибка одного измерения(формула Гаусса).

Имея ряд измерениий одной и той же величины мы должны уметь оценивать точность, как одного измерения, так и арифметической середины. Для оценки точности измерения применяют различные числовые характеристики, одной из таких характеристик является средняя квадратическая ошибка веденная Гауссом. . Cледует помнить , что mкак и др. числовые хар-ки,не ошибка какого-либо измерения, а ср.кв. величина таких ошибок. Вычисление среднеквадратической ошибки по формуле Гаусса возможно только тогда, когда известны истинные ошибки измерений, однако в большинстве случаев они не известны. Поэтому на практике задача решается через уклонения результатов измерений от их арифметического среднего v (вероятнейшие ошибки), которые вычисляются по результатам многократных измерений.