Тема 3 транспортНа задача лінійного програмування

3.1 Значення й економіко-математичне формулювання транспортної задачі

На транспорті, у постачальницько-збутових і торговельних організаціях має важливе місце зниження витрат на перевезення вантажів як на магістральних шляхах так і на промисловому, внутрішньозаводському транспорті. На багатьох підприємствах плани прикріплення постачальників до споживачів, одержувані експертним порядком, досить часто не дають мінімуму транспортних витрат, а іноді досить далекі від оптимального плану. При цьому питома вага транспортних витрат у ціні окремих видів продукції становить досить значну величину, наприклад: солі - 60%, залізної руди - 35%, вугілля - 20%, нафти - 15% []. Тому впровадження математичних методів й ЕОМ у планування перевезень є необхідністю. Основною математичною моделлю, що використовується для складання оптимальних планів поставок і вантажних перевезень є транспортна задача лінійного програмування. Застосування транспортної задачі дозволяє скоротити витрати на перевезення на 5-7% []. З використанням транспортної задачі в МІІТі складені схеми нормальних вантажопотоків різних вантажів []. Транспортна задача застосовувалась у ЛІІЖТі та БелІІЖТі при організації поставок місцевих вантажів (дрова, торф) []. На залізничному транспорті транспортна задача застосовується при плануванні порожніх вагонопотоків [].

У загальному виді транспортна задача формулюється наступним чином.

Задано транспортну мережу з s вершинами (станціями) і e дугами (шляхами між станціями). Позначимо безліч постачальників A, безліч споживачів B, безліч проміжних вершин Т. Для кожної дуги ij задана вартість перевезення c_ij і пропускна здатність d_ij. Нехай a_i - потужність постачальника iA, b_j - попит споживача jB. Потрібно прикріпити споживачів до постачальників таким чином, щоб загальна вартість перевезень була мінімальною . При цьому повинні бути виконані обмеження:

Кількість вантажу, вивезеного з пункту виробництва, повинна рівнятися кількості завезеного й виробленого вантажу (див. мал. 1.1.).

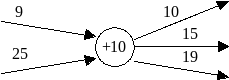
Рис. 1.1.

Кількість вантажу, завезеного в пункт споживання, повинна рівнятися кількості вивезеного й спожитого вантажу (див. мал. 1.2.):

Рис. 1.2.

Кількість вантажу, завезеного в транзитний пункт повинна рівнятися кількості вивезеного з нього вантажу (див. мал. 1.3.):

(1.1)

Рис. 1.3.

Потоки на дугах не повинні перевищувати їх пропускну здатність:

(1.2)

Обсяг виробництва повинен рівнятися обсягу споживання:

(1.3)

Транспортна задача може мати дві форми: закрита, коли виконується обмеження (1.3 і відкрита, коли ця умова не дотримується. При рішенні відкритої транспортної задачі її зводять до замкнутої, додаючи фіктивні пункти виробництва або споживання:

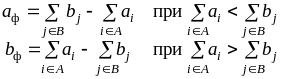(1.4)

Транспортна задача може бути вирішена як у мережевій постановці, так й у матричній. Методи рішення в тім й іншому випадку мають свої переваги й недоліки. Матричний метод досить простий і не вимагає великої кількості обчислень. Існують формальні методи одержання початкових планів на матриці досить близьких до оптимального. У міру збільшення розмірів задачі число ітерацій збільшується приблизно в лінійній залежності від кількості рядків. Мережевий метод дозволяє врахувати пропускну здатність окремих ділянок полігона. Транспортна задача в матричній формі дозволяють урахувати тільки пропускну здатність приймальних пунктів. Транспортні задачі на мережі вимагають менше часу на підготовчі операції, тому що не вимагають визначення найкоротших відстаней між пунктами виробництва й споживання.