16

ИМИТАЦИЯ ПРИ ИЗУЧЕНИИ СЛУЧАЙНЫХ процессов

Как отмечалось во введении, термин «имитационное моделирование» возник первоначально в теории вероятности и математической статистике. Этим термином обозначался способ вычисления статистических характеристик случайного процесса путем многократного воспроизведения его реализаций. Настоящая глава посвящена описанию этого аспекта имитационного моделирования. Она начинается с напоминания основных понятий теории вероятности, математической статистики, теории случайных процессов. В ней излагаются некоторые задачи теории массового обслуживания, которые решаются аналитическими средствами. Приводится достаточно простая задача теории массового обслуживания, которая аналитическими средствами не решается. Описывается ее решение средствами имитационного моделирования.

4.1. Случайные и детерминированные процессы

Вероятностное описание рационально использовать для процесса, который можно многократно воспроизводить, создавая соответствующие условия, или который многократно воспроизводится в реальности независимо от чьей-либо воли. При этом нам заранее известно множество S = {1,2,...,n} конечных состояний этого процесса, известно, что каждое состояние s_i появляется при воспроизведениях процесса с одинаковой относительной частотой, однако мы не можем или не хотим явно описывать все, что приводит к тому или иному состоянию s_i из множества S = {1,2,..., n}, в частности все внешние факторы, которые на это влияют. В этом случае каждому состоянию s_i из S = {1,2,...,n} приписывают число p_i — относительную частоту появления этого состояния при много кратных воспроизведениях процесса, так, что , i=1..,n, , и: называют его вероятностью состояния s_i..Один и тот же процесс может быть и вероятностным, и детерминированным. Это зависит от того, какие именно характеристики процесса нас интересуют, какой уровень подробности представления этих характеристик, а также точность их определения нам необходим. Представим, что некто бросает монету с частотой, например, 1 раз в 10 с и делает это непрерывно и так долго, как потребуется в следующих рассуждениях. Пусть нам необходимо определить функцию, указывающую для каждого момента времени, сколько раз в расчете на временную единицу вокруг данного момента времени выпадает орел. Если временная единица по порядку величины составляет сутки и точность ответа должна составлять 10 %, то интересующую нас величину в каждый момент времени можно считать детерминированной. Эта величина не изменяется со временем и равна (если монета симметрична) 4320 (в сутках 86400 с). Если же временная единица порядка нескольких десятков секунд, и нам по-прежнему необходимо знать ответ с точностью 10 %, то интересующая нас величина в каждый момент времени случайна и может принимать в разные моменты различные значения.

Изложенное положение носит достаточно общий характер. Является изучаемый процесс случайным или детерминированным, зависит от точки зрения, определяемой выбором характерных масштабов осреднения величин модели (по-видимому, нам никогда не будет известно, являются ли реальные процессы «принципиально» детерминированными или «принципиально» вероятностными).

4.2. Случайные величины и их характеристики

Во многих случаях с исходами s_i случайного процесса естественным образом связываются числа x_i. Собственно говоря, во многих случаях исходы s_i и есть некоторые числа x_i. В этом случае говорят о случайной величине X, могущей принимать значения {x₁ ,…х_п} с вероятностями соответственно {р₁,...,р_п}. Функцией распределения (или законом распределения) случайной величины X называют вероятность Р(х) того, что случайная величина примет значение, меньшее х. Математическим ожиданием М случайной величины X называют ее среднее значение, подсчитываемое по формуле

.

Центральным моментом порядка случайной величины X называют математическое ожидание М[(Х — М[Х])²} случайной величины (X — М[Х])². Наиболее употребителен центральный момент D[X] порядка 2, подсчитываемый по формуле

и называемый дисперсией.

Средним квадратичным отклонением [Х] случайной величины называется корень квадратный из дисперсии. Математическое ожидание и среднее квадратичное отклонение случайной величины — ее наиболее важные характеристики. Они дают представление о «положении» случайной величины и о ее «разбросанности».

До сих пор рассматривались так называемые дискретные случайные величины, которые могут принимать лишь конечное (либо бесконечное, но счетное) множество значений. Задание для каждого значения случайной величины вероятности, с которой это значение принимается, называется рядом распределения. Иногда бывает удобно считать, что случайная величина X может принимать бесконечно много значений из некоторого множества действительных чисел. Например, тогда, когда п велико, вероятности p_i малы и количество значений, которое может принять величина X на промежутке (a,b) длины , совпадающем по порядку величины с точностью, с которой желательно или возможно знать величину X, велико. В этом случае ее уже нельзя описывать рядом распределения, и ее исходной характеристикой становится функция распределения X, определяемая точно так же, как это было сделано выше, т. е. Р(х) есть вероятность того, что случайная величина примет значение, меньшее х. Если эта функция непрерывна, то случайная величина называется непрерывной. Вероятность любого отдельного значения непрерывной случайной величины равна нулю, и поэтому для непрерывных случайных величин имеет смысл говорить лишь о вероятности того, что ее значение принадлежит некоторому множеству, мера которого не равна нулю. Вероятность того, что значение х случайной величины X принадлежит множеству [а, b), равна Р(b) — Р(а).

Если функция распределения X непрерывной случайной величины X является дифференцируемой, то удобно оперировать ее плотностью распределения р(х) = dP(x)/dx, также являющейся исчерпывающей характеристикой случайной величины. Вероятность того, что случайная величина примет значение из промежутка (х,х + dx) малой длины dx, равна p(x)dx + o(dx). Для непрерывной случайной величины, обладающей плотностью распределения, математическое ожидание М[Х] и дисперсия D[X] определяются следующим образом:

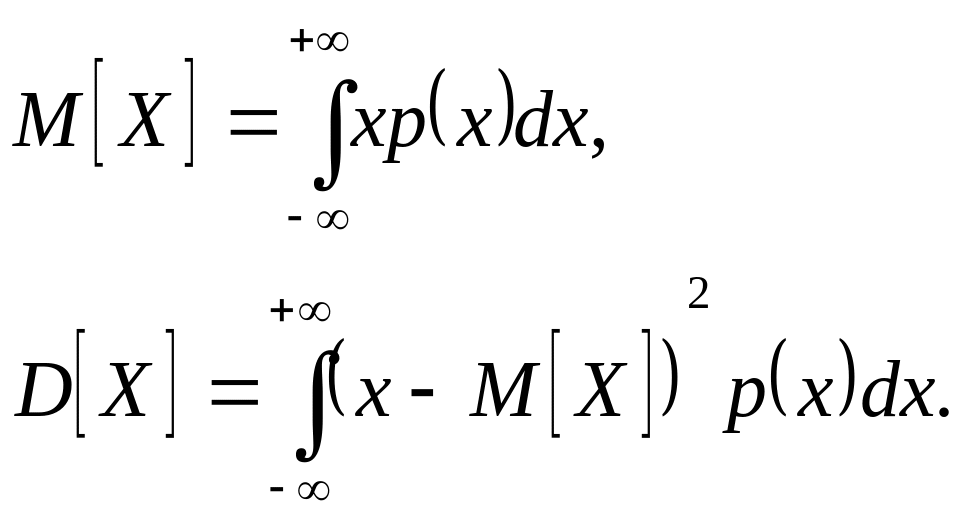
Непрерывная случайная величина, плотность распределения р(х) которой дается формулой

называется распределенной по нормальному закону. Очень многие реальные случайные величины распределены по нормальному закону. Природа этого факта состоит в том, что нормальное распределение является пределом суммы независимых случайных величин, распределенных по произвольным законам (необходимо выполнение некоторых весьма нежестких ограничений) при стремлении количества этих независимых случайных величин к бесконечности. Многие реальные случайные величины являются как раз суммами большого количества слабо зависимых случайных величин. Математическое ожидание случайной величины, распределенной по нормальному закону, равно т, среднее квадратичное отклонение — .

Дискретная случайная величина X, могущая принимать значения из множества натуральных чисел N = {0,1,2,...}, ряд распределения которой дается формулой

(4.1)

где а — постоянный параметр; р(т) — вероятность того, что случайная величина примет значение т, называется распределенной по закону Пуассона.

Многие реальные случайные величины распределены по закону Пуассона. Природа этого факта состоит в следующем. Пусть производится п независимых опытов, в каждом из которых некоторое событие А появляется с вероятностью q. Пусть X — случайная величина, значение которой есть число m появлений события А в п опытах. Ряд распределения величины X дается формулой

. (4.2)

Распределение (4.1) является предельным для распределения (4.2), когда число опытов n стремится к бесконечности, а вероятность q появления события А в каждом опыте стремится к нулю, однако так, что произведение (n*q) стремится к а. Многие реальные случайные величины являются результатом осуществления очень большого числа опытов, в каждом из которых вероятность появления некоторого события весьма мала.

Математическое ожидание и дисперсия случайной величины, ряд распределения которой задается законом Пуассона, равны а.

Математическая статистика занимается разработкой методов регистрации, описания, анализа экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений. Здесь коснемся только одной из ее задач — задачи экспериментального определения числовых характеристик случайных величин. Пусть произведено n опытов, в результате которых получено множество {x₁,x₂, ...,х_п} значений случайной величины X. Естественно оценить математическое ожидание этой величины по формуле

(4.3)

а дисперсию — по формуле

. (4.4)

Пусть истинные математическое ожидание и дисперсия случайной величины X равны, соответственно, М[Х] и D[X]. Рассмотрим величины М*[Х] и D*[Х] как случайные, определенные формулами (4.3) и (4.4) соответственно. Математическое ожидание величины М*[Х] равно М, а математическое ожидание величины D*[X] равно . Эти факты принято выражать следующим образом. Экспериментальная оценка (4.3) математического ожидания является несмещенной, а экспериментальная оценка (4.4) дисперсии является смещенной: если повторять много раз серию из п опытов, получая каждый раз экспериментальные значения случайной величины X и вычислять каждый раз значение D* [X], то оно будет колебаться не вокруг истинного значения дисперсии D, а вокруг значения Несмещенная оценка величины дисперсии дается формулой

(4.5)

Часто на практике возникает не только задача экспериментального вычисления числовых характеристик случайных величин, но и задача оценки точности и надежности этого вычисления. Пусть по экспериментальным наблюдениям случайной величины вычислена оценка (4.3) ее математического ожидания. Обозначим через вероятность того, что величина М*[Х] отклонится от истинного математического ожидания не более чем на . Величину называют доверительной вероятностью, а интервал (М*[Х] — , М*[Х] + ) называют доверительным. Доверительный интервал характеризует точность полученного результата, а доверительная вероятность — его надежность. Задав число , можно по имеющимся экспериментальным результатам оценить вероятность попадания вычисленного значения М* [X] в доверительный интервал.