Московский Государственный педагогический Университет

им. В.И.Ленина

Комплексные числа в планиметрии

(Курсовая работа)

Подготовила: студентка III курса

Маематического факультета

Ильичёва Мария В.

Научный руководитель: доцент

Иванов Иван И.

Москва, 2000

Содержание

Введение……………………………………………………………………….3

1. Геометрическая интерпретация комплексных чисел. Длина отрезка…….4

2. Параллельность и перпендикулярность. Коллинеарность трех точек……8

3. Углы и площади. Критерий принадлежности четырех точек одной окружности…………………………………………………………………..14

4. Подобные и равные треугольники. Правильный треугольник…………...18

5. Прямая и окружность на плоскости комплексных чисел…………………22

6. Две прямые. Расстояние от точки до прямой………………………………24

Заключение…………………………………………………………………...30

Список использованной литературы……………………………..………....31

Введение

Большое значение комплексных чисел в математике и ее приложениях широко известно. Особенно часто применяются функции комплексного переменного. Их изучение имеет самостоятельный интерес. Вместе с тем алгебру комплексных чисел можно успешно использовать в элементарной геометрии, тригонометрии, теории геометрических преобразований, а также в электротехнике и различных задачах с механическим и физическим со­держанием.

Метод комплексных чисел позволяет решать планиметрические задачи по готовым формулам прямым вычислением, элементарными выкладками. Выбор этих формул с очевидностью диктуется условиями задачи и ее тре­бованием. В этом состоит необычайная простота этого метода по сравнению с координатным, векторным и другими методами, требующими от решающе­го порой немалой сообразительности, длительных поисков, хотя готовое ре­шение может быть очень коротким.

В данной работе излагаются основы метода комплексных чисел в при­менении к задачам элементарной геометрии на плоскости и доказательству некоторых основных планиметрических теорем.

Конечно, одна работа не может вместить все существующие теоремы и задачи. Здесь будут рассмотрены лишь некоторые темы, по каждой из которых будет решен ряд задач, наиболее наглядно показывающих простоту этого метода.

Геометрическая интерпретация комплексных чисел. Длина отрезка

При заданной прямоугольной декартовой системе координат на плоскос­ти комплексному числу z = x+iy (i²= -1) можно взаимно однозначно по­ставить в соответствие точку М плоскости с координатами х, у (рис.1):

.

Число z тогда называют комплексной координатой точки М.

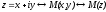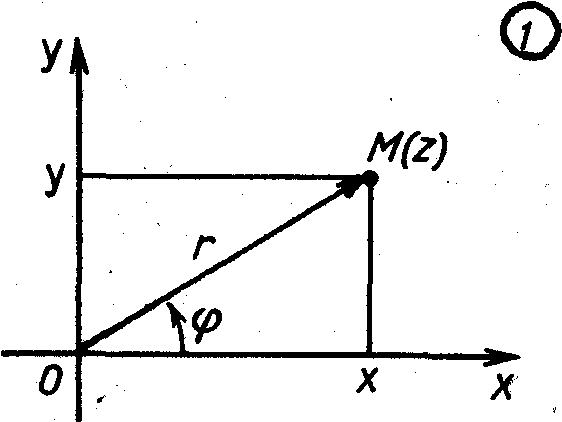
Поскольку множество точек евклидовой плоскости находится во взаим­но однозначном соответствии с множеством комплексных чисел, то эту плос­кость называют также плоскостью комплексных чисел. Начало О декартовой системы координат называют при этом начальной или нулевой точкой пло­скости комплексных чисел.

При у=0 число z действительное. Действительные числа изображаются точками оси х, поэтому она называется действительной осью. При х=0 число z чисто мнимое: z=iy. Мнимые числа изображаются точками оси у, поэтому она называется мнимой осью. Нуль - одновременно действительное и чисто мнимое число.

Paccтoяниe от начала О плоскости до точки М(z) называется модулем комплексного числа z и обозначает­ся |z| или r:

|z| = r = |OM| = .

Если — ориентированный угол, образованный вектором с осью х, то по определению функции синуса и косинуса

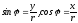
откуда и поэтому .

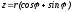Такое представление комплексного числа z называется его тригонометри­ческой формой. Исходное представление z=x+iy называют алгебраичес­кой формой этого числа. При тригонометрическом представлении угол называютаргументом комплексного числа и обозначают еще через arg z:

.

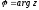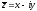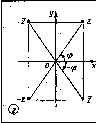
Если дано комплексное число z=x+iy, то число называетсякомплексно-сопряженным (или просто сопряженным) этому числу z. Тогда, очевидно, и число z сопряжено числу . Точки М(z) и 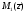симметричны относительно осих (рис.2).

Из равенства 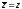следуетy=0 и обратно. Это значит, что число, рав­ное своему сопряженному, является действительным и обратно.

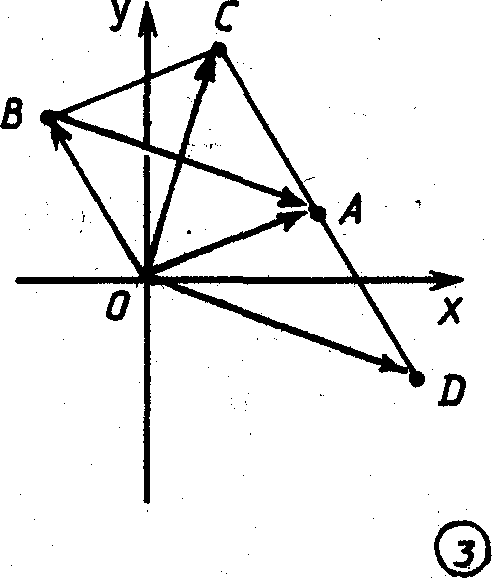
Точки с комплексными координатами z и -z симметричны относитель­но начальной точки О. Точки с комплексными координатами z и 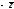сим­метричны относительно оси у. Из равенства z= вытекает x=0 и об­ратно. Поэтому условие z=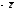 является критерием чисто мнимого числа.

Для любого числа z, очевидно, |z| = || = |-z| = ||.

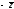Сумма и произведение двух сопряженных комплексных чисел являются действительными числами: .

Число, сопряженное с суммой, произведением или же частным комплекс­ных чисел, есть соответственно сумма, произведение или же частное чисел, сопряженных данным комплексным числам:

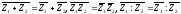
Эти равенства можно легко проверить, пользуясь формулами для опе­раций над комплексными числами.

Каждой точке М(z) плоскости - взаимно однозначно соответствует век­тор 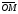. Поэтому комплексные числа можно интерпретировать векторами, приложенными к точке O. Сложению и вычитанию комплексных чисел отвечает сложение и вычитание соответствующих им векторов. Именно если а и b - комплексные координаты точек A и В соответственно, то число с=а+b является координатой точки С, такой, что (рис.3). Комплексному числу d=a-b соответствует такая точка D, что .

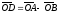Расстояние между точками А и В равно :

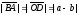|АВ| = |а-b|. (1)

Так как |z|²= z, то

|AB|²=(a-b)(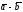).(2)

Уравнение z= r² определяет окружность с центром О радиуса r. Отношение 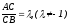, в котором точка С делит данный отрезок АВ, выражается через комплексные координаты этих точек так:

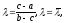
откуда 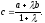(3)

Если положить 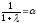и, то

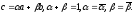(4)

Условия (4) необходимы и достаточны для того, чтобы точки А, В, С были коллинеарны.

При 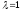точка С является серединой отрезка AB, и обратно.

Тогда:

c = 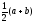.(4a)

Пусть имеем параллелограмм ABCD. Его центр имеет комплексную координату 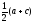= 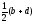при условии, что точки А, В, С, D имеют соответственно комплексные координаты а, b, с, d. Если не исключать случай вырождения параллелограмма, когда все его вершины оказываются на одной прямой, то равенство

a+c = b+d (5)

является необходимым и достаточным условием того, чтобы четырехуголь­ник ABCD был параллелограммом.

Задача 1. Точки М и N — середины диагоналей АС и BD четырех­угольника ABCD. (Рис.1)

Доказать, что |AB|²+|BC|²+|CD|²+|DA|² = |AC|²+|BD|²+4|MN|².

Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b, с, d, т, п.

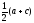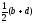Так как m = и n = ,то

|AB|²+|BC|²+|CD|²+|DA|²

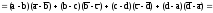
|AC|²+|BD|²+4|MN|²

.

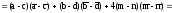
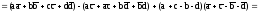
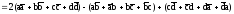Равенство доказано.

Задача 2. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, что |MA|²+|MC|²=|MB|²+|MD|², тo ABCD - прямоугольник. (Рис.2)

Решение. Если за начальную точку принять центр параллелограм­ма ABCD, то при принятых ранее обозначениях с= -a, d= -b, и поэтому данное в условии равенство будет эквивалентно равенству 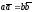, которое означает, что диагонали параллелограмма равны, т. е. он прямоугольник.

Задача 3. Доказать, что сумма квадратов диагоналей AC, BD четырехугольника ABCD равна удвоенной сумме квадратов отрезков MN, PQ, соединяющих середины противополож­ных сторон . (Рис.3)

C

B B C

M(O)

N M MЬ

A D A D

Рис. 1 Рис. 2

Решение. Требуется доказать:

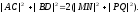
Запишем левую часть равенства в комплексной форме: 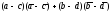. Воспользовавшись (4a), находим комплексное равенство правой части и непосредственным подсчетом убеждаемся, что она равна левой.

B

P

C

M

N

A

Q D

Рис. 3

Задача 4. Доказать, что сумма квадратов медиан BM, AN, CP треугольника ABC равна 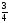суммы квадратов его сторон. (Рис.4)

Решение. Требуется доказать: Запишем левую часть, воспользовавшись формулами (2) и (4а), и убедимся в том, что она равна правой.

Задача 5. Доказать, что расстояние от вершины С треугольника АВС до точки D, симметричной центру описанной окружности относительно прямой АВ, вычисляется по формуле |CD|²=R²+|AC|²+|BC|²-|AB|², где R -радиус описанной окружности. (Рис.5)

Решение. Точка M является серединой АВ, так как центр описанной окружности лежит на пересечении серединных перпендикуляров.

Точка М - середина ОD (по условию).

Тогда, 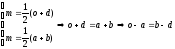. Воспользуемся этим равенством, формулами (2) и (4а) и убедимся в справедливости|CD|²=R²+|AC|²+|BC|²-|AB|².

B B

N

P

A

C

A M C

Рис. 4 Рис. 5