Лекция 30

Динамические свойства э-опривода пост. и переменного тока с линейной мех-кой хар-кой при различных способах управления. Э-омех-кая постоянная времени и ее физический смысл. Э-омагнитная постоянная времени, исследование ПП-сов с ее учетом. Elektroprivod – 195стр.

(Н.Ф. ИЛЬИНСКИЙ ОСНОВЫ Э-ОПРИВОДА lek 5). При мгновенном изменении f₁ и U₁ мгновенно устанавливается новая механическая хар-ка, а изменение скорости  и момента М в переходном процессе происходит согласно этой хар-ке. Переходный процесс определяется статической механической хар-кой привода.

При частотном изменении f₁ и U₁ переход привода с одной хар-ки на другую происходит постепенно, одновременно с изменением скорости, в результате чего соответствие между скоростью  и моментом М в каждый момент времени определяется не статической механической хар-кой, а другой, отличной от нее хар-кой, которую называют динамической механической хар-кой или просто динамической хар-кой.

В качестве примера на рис. 5.13 показана статическая хар-ка АД при номинальной частоте 1, по которой будет происходить пуск при мгновенном приложении к двигателю напряжения такой частоты, и динамическая хар-ка 2, соответствующая пуску двигателя путем плавного изменения частоты от нуля до номинальной по некоторому закону.

Рис. 5.13. Статическая 1 и динамическая 2 механические хар-ки

Динамические хар-ки определяются темпом изменения фактора, вызывающего переходный процесс, и пар-ми привода, могут очень сильно отличаться от статических хар-тик и даже иметь совсем другую форму.

Уравнения, описывающие переходные процессы(Ильинский общий курс э-опривода).

Преобразуем уравнение движения (5.12):

(5.13)

Правая часть уравнения представляет собою скорость _с, соответствующую моменту сопротивления М_с, однако, в рассматриваемом случае ₀ , а значит и _с не постоянные величины, а известные функции времени ₀(t) и _c(t). Таким образом, уравнение (5.13) имеет вид:

. (5.14)

Решение этого дифференциального уравнения определит искомую зависимость (t).

Для получения зависимости М(t) удобно воспользоваться непосредственно уравнением движения (5.12), подставив в него производную найденной функции (t):

(5.15)

Правая часть уравнения (5.14), вообще говоря, может иметь любой вид. Закон ₀(t) в случае безынерционного преобразователя формируется на его входе; при инерционном преобразователе закон ₀(t) связан со свойствами преобразователя. В ряде случаев закон ₀(t) формируется таким образом, чтобы получить требуемый закон (t).

Длительность (Чекунов 90) протекания переходных процессов определяется соответствующими постоянными времени. Так, механическая инерция характеризуется Э-омеханической постоянной времени Т_м . Для ДПТ она представляет собой время, в течение которого привод с моментом инерции J разгоняется вхолостую из неподвижного состояния до скорости идеального ХХ при неизменном моменте, равном моменту короткого замыкания.

Э-омагнитные переходные процессы обусловлены изменением запаса э-омагнитной энергии в электрических машинах, пропорциональных индуктивности их цепей и квадрату протекающего по ним тока. Длительность определяется индуктивностью обмоток.

Э-омагнитная инерция хар-ется э-омагнитной постоянной времени Т_э,(или Т_в), равной отношению индуктивностей L электрич. цепей привода к их активному сопротивлению: Т_э= L/R. Физический смысл э-омагнитной постоянной времени: это время, в течение которого ток в контуре, содержащем индуктивность, изменяется от нуля до установившегося значения, определяющегося величиной приложенного напряжения и омического сопротивления контура.

Если к зажимам обмотки, обладающей индуктивностью L­_В и омическим сопротивлением R­_В, приложить постоянное напряжение U­_В­, то уравнение ЭДС для цепи, например, обмотки возбуждения ДНТ выразится следующим образом:

Разделив правую и левую части на R­_В, получим диф. уравнение первого порядка

где: ;

Решение уравнения для общего случая, когда при t = 0 начальное значение тока i = I­_нач­:

Т.о. закон изменения тока носит экспоненциальный характер. Продолжительность переходного процесса приблизительно (3÷4)T­_В. Полученные уравнения не учитывают насыщение магнитной системы, т.е. считают L = const.

Ориентировочно T­_В – двигателя независимого возбуждения

, с.

При Р = (1 ÷ 100) кВт → T­_В­ = (0,1 ÷ 1) с

Р = (100 ÷ 1000) кВт → T­_В­ = (1 ÷ 2) с

Р = (1000 ÷ 3000) кВт → T­_В­ = (2 ÷ 4) с

Поэтому продолжительность нарастания тока может быть значительной (3÷4)T­_В , что приводит к уменьшению быстродействия. Для сокращения времени переходного процесса применяют форсировку возбуждения – различные способы ускорения нарастания тока возбуждения.

Проведем анализ электромеханической системы, состоящей из двигателя с линейной механической хар-кой, и жест­кoгo механического звена. Движение такой электромеханической системы определяет­ся уравнением движения электропривода

(1)

Линейная механическая характеристика описывается ypaвнением

. (2)

Совместное решение (1) и (2) позволяет получить ypaвнение, описывающее переходные процессы двигателя, опреде­ляемые механической инерционностью электропривода

. (3)

Из других источников (Н.Ф. ИЛЬИНСКИЙ ОСНОВЫ Э-ОПРИВОДА lek 5)берут модуль величины, стоящей в знаменателе . Величину, стоящую перед производной,

называют э-омеханической постоянной времени. Физический смысл: представляет собою время, за которое привод разогнался бы вхолостую до  = ₀ под действием момента короткого замыкания.

Величина представляет собой падение скорости от нагрузки –­ статическую ошибку , а величина ­– установившееся значение скорости после окончания переходного процесса, когда М станет равным Мс (см.рис.8.3,а).

Рис.8.З. Переходный процесс пуска э-опривода:1–механич. и 2 –переходная хар-ка

Тогда, обозначив

получим выражение для переходной хар-ки э-опри­вода:

.

Переходные процессы, определяемые одной механической инерционностью, суммарным приведенным к валу двигателя моментом инерции описываются ДУ первого порядка. Решением этого уравнения является пере­ходная хар-ка, имеющая вид экспоненты с постоянной

времени Т_М (см. рис.8.3,б):

.

:

.

Ток, момент и скорость двигателя с линейной механической хар-кой в переходных режимах изменяются по экспоненциальному закону.

Динамические хар-ки э-опривода постоянного тока по системе тиристорный преобразователь - ДПТ (ТП­-Д). Elektroprivod – 195стр 7777777777777

Э-омагнитная постоянная времени, исследование переходных процессов с ее учетом.

(общий курс эопривода Ильинский). Переходный процесс в э-оприводе с ДПТ независимого возбуждения при L_я0.

Рассмотрим схему на рис. 5.19. Отличительной особенностью схемы по сравнению с рассмотренными ранее является индуктивность L_я. Для якорной цепи справедливо уравнение:

, (5.23)

решив которое относительно :

(*)

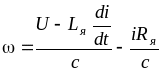и обозначив получим

. (**)

Рис. 5.19. Схема пуска э-опривода постоянного тока с двигателем

независимого возбуждения

U зависит от т.е. уравнение (**) представляет семейство прямых (рис. 5.20,а), параллельных естественной хар-ке и располагающихся как ниже ( > 0), так и выше ( < 0) нее. При = 0, очевидно, уравнение (**) соответствует естественной хар-ке.

После замыкания ключа К ток i начинает расти, значит растет М и привод разгоняется (для упрощения рассуждений примем М_с = 0), переходя при этом с характеристики на на характеристику ( > 0, но уменьшается по мере разгона). В процессе увеличения тока и скорости (участок Оа на рис. 5.20) возрастает запас энергии как в индуктивности, так и во вращающемся якоре. В точке а рост тока прекращается; при этом в соответствии с (*) привод оказывается на естественной характеристике, но М > М_с = 0. С точки а начинается спадание тока, т.е. энергия, запасенная в L_я, передается вращающемуся якорю. Механизм передачи очевиден из (*): напряжение, приложенное к якорю U, становится больше, чем напряжение сети U. На участке аb привод разгоняется, соответственно растет е = с, причем в точке b i = 0 – запас энергии в L_я исчерпан, однако  >₀ и e > U, т.е. в якоре запасена избыточная механическая энергия.

На участке bc под действием e > U ток изменяет направление, привод тормозится, при этом избыточная механическая энергия вновь переходит в электромагнитную энергию, накапливаемую в индуктивности. В точке с = 0, однако в L_я запасена энергия, чему соответствует i  0 и M  0. Привод продолжает тормозиться до точки d, затем процесс повторяется.

Кривая 0abcd... ₀ в плоскости  – M представляет собою динамическую механическую хар-ку. Соответствующие зависимости (t), i(t) или M(t) показаны на рис. 5.20,б.

а) б)

Рис. 5.20. Механические хар-ки (а) и переходной процесс пуска при L_я  0 (б)

Колебательность процесса связана с тем, что происходит периодическое преобразование кинетиче­ской энергии в эомагнитную и обратно.

Так как в якорной цепи есть сопротивление R_я процесс перекачивания энергии сопровождается ее рассеиванием, вследствие чего система после ряда колебаний приходит в точку ₀, соответствующую установившемуся режиму. Если бы сопротивление R_я было равным нулю, колебания  и М имели бы незатухающий характер. Если, наоборот, R_я велико, энергии, запасенной в L_я на участке 0а, может оказаться недостаточно для покрытия потерь в R_я и вывода якоря в точку  > ₀ при i = 0. В этом случае процесс будет иметь апериодический хар-р.

Для определения возможности колебательного процесса составляется характеристическое уравнение

1 + Т_мр + Т_мТ_яр² = 0 (^)

Определяются его корни p₁, p₂

=

откуда вытекает условие колебательности процесса. Если

т.е. Т_м < 4Т_я,

корни комплексные и процесс носит колебательный характер; если

т.е. Т_м  4Т_я,

корни действительные и процесс апериодический.

Рис.8.6. Переходные хар-ки э-опривода с линейной механической хар-кой при пуске