Цилиндрлік қисықсызықты фигураның Жордан бойынша өлшемділігі
Үш өлшемді фигураның Жордан бойынша өлшемділік ұғымымен байланысты анықтаманы еске аламыз.
Анықтама 10. Егер фигура , қабырғалары координат өстеріне параллель ақырлы санды параллелепипедтердің бірігуі болса, онда оны қарапайым деп атайды. Мұндай параллелепипедтерді стандартты деп атайды.
кеңістігіндегі
барлық қарапайым фигуралардың жиынын
арқылы белгілейміз. Қарапайым фигураның
Жордан өлшемі (немесе көлемі) – бұл осы
фигураны бөлуге болатын, ашық қиылыспайтын
стандартты көлемдердің қосындысы.
Анықтама
11. Шектелген
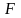фигураның Жорданның
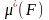жоғарғы өлшемі деп
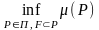шамасын айтады, яғни
-ті
құрайтын барлық қарапайым фигуралардың
көлемдерінің нақты төменгі жағы. Осыған
ұқсас,
фигураның
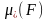Жорданның
шамасын айтады. Егер
болса, онда
фигурасы Жордан бойынша өлшемді деп
атайды және оның Жордан өлшемі (көлемі)
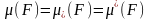-ке
тең. Әрбір жазықтықтың шектелген
бөлігінің көлемі әрқашан нөлге тең
екенін ескереміз. Жордан бойынша
фигураның өлшемділік критерийін еске
аламыз.
фигураның шекарасын
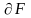арқылы белгілейміз, яғни
фигура үшін ішкі емес, сыртқы емес
-гі
нүктелер жиыны.
Теорема
4. Жордан бойынша
фигураның өлшемділігі үшін , оның
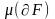шекарасының өлшемі нөлге тең болуы
қажетті және жеткілікті. Бұл критерийдің
дәлелденуін келтірмей-ақ қояйық, өйткені
оның дәлелдеуі екі өлшемді жағдайдың
дәлелдеуінен айырмашылығы жоқ. Тек
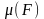шамасының келесі 4 қасиетін атап өтейік:
1) Егер
және
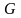өлшемді болса, онда
және
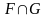фигуралары
өлшемді;
2) Егер
және
қиылыспаса, онда
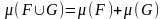(аддитивтілік қасиет);
3) Егер
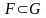болса, онда
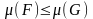(монотондық қасиеті);
4) фигураның өзгерісі мен бұрылысы бұл фигураның өлшем мәнін өзгертпейді (инварианттылық қасиеті).
Теорема
5. Тіктөртбұрыштағы шектелген
функциясының интегралдануы үшін,
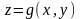бетіне жауап беретін цилиндрлік
қисықсызықты
фигура Жордан бойынша өлшеді болуы
қажетті және жеткілікті.
Дәлелдеуі.
Қажеттілік.
функциясы
-да
интегралданатын болсын.
фигураның өлшемді екенін дәлелдеу
керек. Бұл фигураның
шекарасы 6 беттен тұрады:
,
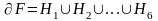мұндағы
-
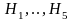координат жазықтықтарына параллель
жазықтықтар бөліктерінен тұратын
фигураның шекарасының бөліктері және
,
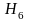беті.
,
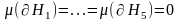өйткені әрбір тіктөртбұрыш немесе оның
бөлігі нөлдік көлемге ие болады.
функциясының Риман бойынша интегралдану
критерийінен
.
Олай болса, кейбір
үшін, мынадай
бөліну табылып,
теңсіздігі орынды. Бұл
бөліну үшін,
тіктөртбұрышының
бөлінуіне сәйкес келетін, тұйық
параллелепипедтердің (брустардың)
бірігуі болатын қарапайым
фигурасын қарастырамыз. Әрбір
брус мынадай
нүктелерден тұрып, барлық
үшін,
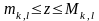(мұндағы
).
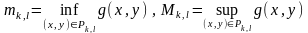Онда, фигура
,
бетінің барлық нүктелерін құрайды.
Содан ,
.
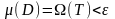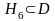болғандықтан,
.
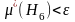еркін
болғандықтан
.
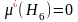Бұдан,
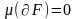шығады, сонда өлшемділік критерийіне
байланысты
фигурасы Жордан бойынша өлшемді.
Дәлелденді.
І текті меншіксіз интеграл
ІІ текті қисықсызықты интегралдың қасиеттері
ІІ текті меншіксіз интегралдар