- •Беттік интегралдар
- •Беттің ауданы
- •Грин формуласы
- •Қисықсызықты интегралдың қасиеттері
- •2) Екінші текті интегралды (1.1) нүктесіне жүргізілген түзусызықты
- •Қос интегралдан қайталанғанға ауысу
- •Қос интегралдың негізгі қасиеттері
- •Лебег критерийі
- •Потенциалды және соленоидалды векторлық
- •Цилиндрлік қисықсызықты фигураның Жордан бойынша өлшемділігі
2) Екінші текті интегралды (1.1) нүктесіне жүргізілген түзусызықты
кесінді
бойымен және осы нүктелерді қосатын
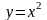 параболасының
доғасы бойынша есептеу керек . Бірінші
жағдайда (y=x) мынаны аламыз:
параболасының
доғасы бойынша есептеу керек . Бірінші
жағдайда (y=x) мынаны аламыз:
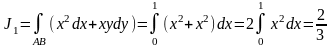 .Екінші
жағдайда
.Екінші
жағдайда
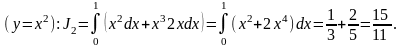
Қос интегралдан қайталанғанға ауысу
Қос және қайталанған интегралдардың теңдігі туралы теореманы құрайық.
Теорема
7. Функция
тіктөртбұрыш
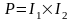 ,
,
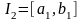 -де
интегралданатын болсын. Сол сияқты бір
айнымалылы у-тің
-де
интегралданатын болсын. Сол сияқты бір
айнымалылы у-тің
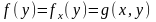 функциясының ке-келген бекітілген
функциясының ке-келген бекітілген
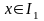 мәні
үшін,
мәні
үшін,
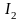 кесіндісінде у бойынша интегралданады
және
кесіндісінде у бойынша интегралданады
және
 .
Сонда мына формуланың орны бар:
.
Сонда мына формуланың орны бар:
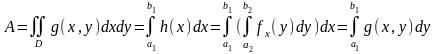 яғни
қос интеграл қайталанған интегралға
тең. Дәлелдеуі.
яғни
қос интеграл қайталанған интегралға
тең. Дәлелдеуі.
Тіктөртбұрыш Р-ның кез-келген T=Tp бөлінуі үшін.
 теңсіздігін
аламыз, мұндағы
теңсіздігін
аламыз, мұндағы
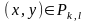 және
және
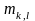 мен
мен
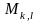 k=1,
…,m;
k=1,
…,m;
l=1, …,n шамаларының дағдылы мағынасы бар.
Бекітілген
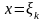 кезінде
бұл теңдікті
кезінде
бұл теңдікті
 -ден
-ден
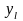 -ге
дейін у бойынша интегралдаймыз. Сонда
-ге
дейін у бойынша интегралдаймыз. Сонда
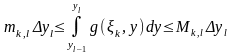
Бұл теңсіздікті l бойынша қарстырамыз.
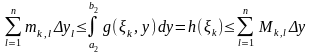
Соңғы
теңсіздікті
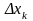 -ға
көбейтіп және оны к бойынша қосып, мынаны
аламыз:
-ға
көбейтіп және оны к бойынша қосып, мынаны
аламыз:
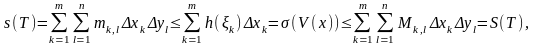
Мұндағы V(x)-I1 кесіндісінің Т бөлінуінің белгісі. Одан басқа
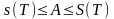
Функция
Р-да интегралданатын болғандықан, онда
кез-келген
саны үшін, мынандай
саны табылады да,
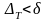 шартымен
әрбір Т бөліну үшін ,
шартымен
әрбір Т бөліну үшін ,
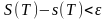 болады.
Бөліну
болады.
Бөліну
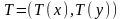 бөліну
жұбынан құрылған: T(x)-Ox осі бойынша,
T(y)- Оу осі бойынша. Бөліну T(x) ретінде
бөліну
жұбынан құрылған: T(x)-Ox осі бойынша,
T(y)- Оу осі бойынша. Бөліну T(x) ретінде
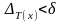 шартымен кез-келген бөлінуді алуға
болады. Бөліну T(x) –тың кез-келген
белгісін аламыз. I1 кесіндісінің V=V(x)
ұсақталған бөлінуін аламыз.
шартымен кез-келген бөлінуді алуға
болады. Бөліну T(x) –тың кез-келген
белгісін аламыз. I1 кесіндісінің V=V(x)
ұсақталған бөлінуін аламыз.
А
және
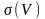 сандарының екеуі де ұзындығы
-ға
тең бір кесіндіде жатады және
сандарының екеуі де ұзындығы
-ға
тең бір кесіндіде жатады және
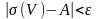 .
Бұл теңсіздік
шартымен кез-келген ұсақталған бөліну
үшін дұрыс. Олай болса, мына теңдіктің
орны бар:
.
Бұл теңсіздік
шартымен кез-келген ұсақталған бөліну
үшін дұрыс. Олай болса, мына теңдіктің
орны бар:
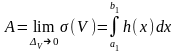
Дәлелденді.
Кез-келген өлшенген D жиыны бойынша интегралдау жағдайы қарастырылғаннан айырмашылығы аз. Тіктөртбұрыш Р D-ны қамтитын болсын. Сонда анықтама бойынша
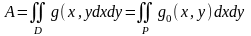 болады,
мұндағы
болады,
мұндағы
 функциясы
D жиынында g функциясымен сәйкес және
D-ның сыртында
функциясы
D жиынында g функциясымен сәйкес және
D-ның сыртында
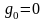 ,
,
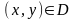 үшін
у нүктелерінің жиынын E(x) арқылы
белгілейміз. E(x) жиыны
үшін
у нүктелерінің жиынын E(x) арқылы
белгілейміз. E(x) жиыны
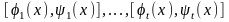 кесінділерінің шектеулі санынан тұрады.
Сонда егер
кесінділерінің шектеулі санынан тұрады.
Сонда егер
 ,
мұндағы
,
мұндағы
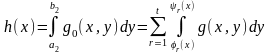
Формуласының орны бар және ол теорема 7-нің тұжырымын жалпылайды.
Қос интегралдың негізгі қасиеттері
 -Жордан
бойынша өлшенетін жиын және
,
-Жордан
бойынша өлшенетін жиын және
, ,
,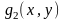 функциялары
қарстырылатын жиындағы Риман бойынша
интегралданады. Онда келесі қасиеттер
орынды болады.
функциялары
қарстырылатын жиындағы Риман бойынша
интегралданады. Онда келесі қасиеттер
орынды болады.
Мына теңдіктер дұрыс:
a)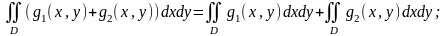
б)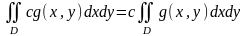 ,
,
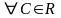 (сызықтық
қасиеті).
(сызықтық
қасиеті).
2) g1 және g2 функциялары D-да интегралданатын болсын, онда g1g2 D-да интегралданады.
3) D-да ≤ теңсіздіктері дұрыс болсын. Бұл жағдайда:
a)
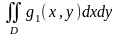 ≤
≤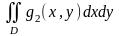 (монотонды қасиеті)
(монотонды қасиеті)
б)
D-да сондай-ақ
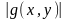 интегралданатын болсын. Онда
интегралданатын болсын. Онда
 ≤
≤
в)
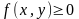 ,
,
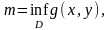
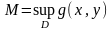 болсын.
Онда мынадай m<c<M,
c
саны
табылып,
болсын.
Онда мынадай m<c<M,
c
саны
табылып,
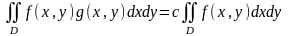
(орта туралы теорема)
4)
 .
.
Бұл тұжырым Жордан өлшемінің және жалпыланған қос интеграл анықтамалаының эквиваленттілігінен шығады.
5)
Егер
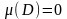 болса, онда D- да шектелген кез-келген
функциясы үшін
болса, онда D- да шектелген кез-келген
функциясы үшін
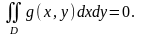
Дәлелденуі:
Функция
D жиынында шектелген болғандықтан, онда
мынадай M>0 саны табылады да, барлық
нүктелері үшін
 теңсіздігі
орындалаы. 3), 1) және 4) қасиеттерден
мынаны аламыз:
теңсіздігі
орындалаы. 3), 1) және 4) қасиеттерден
мынаны аламыз:
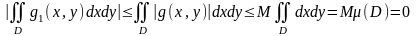 .
Дәлелденді.
.
Дәлелденді.
6)
Облыстар D1
және D2-нің
ортақ ішкі нүктелері жоқ болсын. Онда
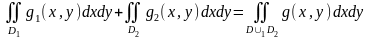 (аддитивтілік
қасиеті)
(аддитивтілік
қасиеті)
Дәлелденуі: Стандартты тіктөртбұрыш D1 және D2 қамтитын болсын. Онда анықтама бойынша
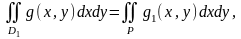
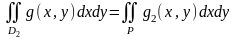
Мұндағы:

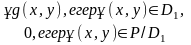
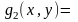
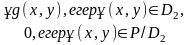
Бұдан және интегралдың сызықтық қасиетінен мынаны аламыз:
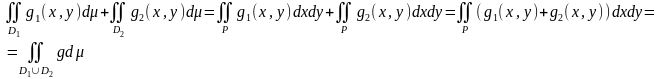 Дәлелденді.
Дәлелденді.
7)
Егер
және
функцияларының мәндері D1 жиынында ғана
айырмашылығы болса, әрі
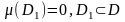 онда
онда
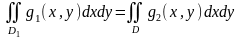
Дәлелденуі.
Шындығында да,