
- •Беттік интегралдар
- •Беттің ауданы
- •Грин формуласы
- •Қисықсызықты интегралдың қасиеттері
- •2) Екінші текті интегралды (1.1) нүктесіне жүргізілген түзусызықты
- •Қос интегралдан қайталанғанға ауысу
- •Қос интегралдың негізгі қасиеттері
- •Лебег критерийі
- •Потенциалды және соленоидалды векторлық
- •Цилиндрлік қисықсызықты фигураның Жордан бойынша өлшемділігі
Грин формуласы
Екінші
текті интегралдың аддитивтілігіне
байланысты кез келген
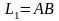 және
және
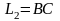 қисықтары
үшін
қисықтары
үшін
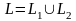 қисығының
еселі нүктелері болмаған жағдайда ,
мынаны аламыз:
қисығының
еселі нүктелері болмаған жағдайда ,
мынаны аламыз:
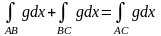 .
.
Осы формула бойынша А және С нүктелері беттескен жағдайда L қисығы бойынша интеграл анықталады .Бұл жағдайда қисықтарының бірігуі тұйықталған қисық деп аталады .
Анықтама 28.Егер
1) ;
2)
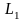 және
-
және
-
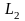 шеттері
беттесетін бөлікті-тегіс қисықтар;
шеттері
беттесетін бөлікті-тегіс қисықтар;
3)
және
қисықтарының басқа жалпы нүктесі
болмасада , онда қисық , тұйық бөлікті
– тегіс қисық (еселі нүктелерсіз) деп
аталады . Егер
қисығында
айналып өту бағыты берілсе , яғни бастапқы
А нүктесі және соңғы В нүктесі берілсе
,және егер
қисығында
бастапқы нүкте ретінде В , ал соңғысы
ретінде А нүктесін алсақ , онда L қисығында
кез келген үш әртүрлі
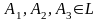 нүктелері
үшін әрқашанда келесі нүктелермен жүру
ретінің
нүктелері
үшін әрқашанда келесі нүктелермен жүру
ретінің
 немесе
немесе
 біреуінің орны бар мағынасындағы
айналып өту бағыты беріледі . Сондықтан
кез келген тұйық L қисықта дәл екі айналып
өту бағыты болады , оның бірін әрине оң
, ал екіншісін теріс деп есептеу керек
.
біреуінің орны бар мағынасындағы
айналып өту бағыты беріледі . Сондықтан
кез келген тұйық L қисықта дәл екі айналып
өту бағыты болады , оның бірін әрине оң
, ал екіншісін теріс деп есептеу керек
.
Сезгеніміздей
, сонымен
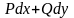 дифференциалдық форманың J интегралы
үшін оң бағытта алынған , тұйық L қисығы
бойынша мынадай белгілеу қолданылады
дифференциалдық форманың J интегралы
үшін оң бағытта алынған , тұйық L қисығы
бойынша мынадай белгілеу қолданылады
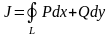 .
.
Тұйық
қисықты айналып өтудің оң бағытын қалай
таңдауға болатынын анықтайық.Алдымен
h шеңбердің
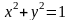 маңызды мысалын қарастырамыз. Шеңберді
айналып өтудің оң бағыты ретінде “сағат
тіліне қарсы айналу бағыты” алынады .
Ол былай анықталады . Шеңберді жоғарғы
жарты шеңбер
маңызды мысалын қарастырамыз. Шеңберді
айналып өтудің оң бағыты ретінде “сағат
тіліне қарсы айналу бағыты” алынады .
Ол былай анықталады . Шеңберді жоғарғы
жарты шеңбер
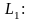
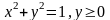 және
төменгі жарты шеңбер
-ге
бөлеміз . Жоғарғы жарты шеңбердің санақ
басы ретінде (1,0) координатасы мен А
нүктесін аламыз және В нүктесін соңғы
нүктесі деп есептейміз . Төменгі жарты
шеңбер
-нің бастапқы нүктесі ретінде В аламыз
, ал соңғы нүктесі деп А нүктесін
есептейміз . Шеңбер L-ге онда А нүктесінде
кез келген еркін алынған жанама
және
төменгі жарты шеңбер
-ге
бөлеміз . Жоғарғы жарты шеңбердің санақ
басы ретінде (1,0) координатасы мен А
нүктесін аламыз және В нүктесін соңғы
нүктесі деп есептейміз . Төменгі жарты
шеңбер
-нің бастапқы нүктесі ретінде В аламыз
, ал соңғы нүктесі деп А нүктесін
есептейміз . Шеңбер L-ге онда А нүктесінде
кез келген еркін алынған жанама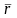 векторды көрсетіп , бірмәнді айналып
өту бағытын беруге болады .
кеңістігінің хОу жазықтығында L шеңберді
қарастырамыз . Оның әрбір нүктесінде
хОу жазықтығында жататын шеңберге
жүргізілген сыртқы нормалдың векторы
n̅ , оған жүргізілген жанама вектор
берілген болсын. Егерде Oz осі бойынша
бағытталған е̅₃
орты
векторды көрсетіп , бірмәнді айналып
өту бағытын беруге болады .
кеңістігінің хОу жазықтығында L шеңберді
қарастырамыз . Оның әрбір нүктесінде
хОу жазықтығында жататын шеңберге
жүргізілген сыртқы нормалдың векторы
n̅ , оған жүргізілген жанама вектор
берілген болсын. Егерде Oz осі бойынша
бағытталған е̅₃
орты
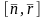 векторлық
көбейтіндімен беттессе , онда вектор
шеңбер
L-дің айналып өту бағытын береді деп
айтамыз . Шеңбердің осы қасиетін жалпы
қисық L-дің айналып өтудің оң бағытының
анықтамасы негізінде аламыз .
векторлық
көбейтіндімен беттессе , онда вектор
шеңбер
L-дің айналып өту бағытын береді деп
айтамыз . Шеңбердің осы қасиетін жалпы
қисық L-дің айналып өтудің оң бағытының
анықтамасы негізінде аламыз .
Анықтама
29 . хОу жазықтығындағы дөңес Д жиынының
шекарасы болатын еселі нүктелерсіз
тұйық бөлікті-тегіс L қисығы болсын .
 Оz
осі бойынша бағытталған орт болсын . L
қисықтың әрбір нүктесіне жанама r̅
вектормен сыртқы нормалдың n̅ векторын
береміз . Егер е̅₃
векторы
векторлық көбейтіндісімен беттессе
, онда L қисығында айналып өтудің оң
бағыты берілген деп айтамыз . Мақсатымыз
,D облысының шекарасы болатын
Оz
осі бойынша бағытталған орт болсын . L
қисықтың әрбір нүктесіне жанама r̅
вектормен сыртқы нормалдың n̅ векторын
береміз . Егер е̅₃
векторы
векторлық көбейтіндісімен беттессе
, онда L қисығында айналып өтудің оң
бағыты берілген деп айтамыз . Мақсатымыз
,D облысының шекарасы болатын
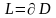 тұйық қисығы бойынша қисықсызықты
интегралмен осы облыс бойынша қос
интеграл арасындағы байланысты
тағайындайтын Грин формуласын
дәлелдейміз.Қарапайымдылық үшін дөңес
D облысы жағдайын қарастырамыз.
тұйық қисығы бойынша қисықсызықты
интегралмен осы облыс бойынша қос
интеграл арасындағы байланысты
тағайындайтын Грин формуласын
дәлелдейміз.Қарапайымдылық үшін дөңес
D облысы жағдайын қарастырамыз.
Теорема 28.(Грин формуласы)
D дөңес
,Жордан бойынша өлшемді,компакт,тұйық
ерекшеленбеген бөлікті-тегіс
қисықтың
шекарасы болсын.Сол сияқты
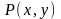 және
және
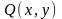 функциялары
D-да үзіліссіз және сонда үзіліссіз
дербес
функциялары
D-да үзіліссіз және сонда үзіліссіз
дербес
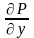 және
және
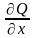 туындысы бар болсын.Онда келесі
формула дұрыс:
туындысы бар болсын.Онда келесі
формула дұрыс:
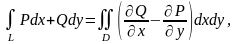 мұндағы
L қисығы оң бағытта айналып
өтеді.Дәлелдеуі.Тек
мұндағы
L қисығы оң бағытта айналып
өтеді.Дәлелдеуі.Тек
 теңдігін дәлелдеу керек.Осыған ұқсас
теңдігін дәлелдеу керек.Осыған ұқсас
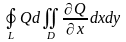 теңдігі дедәлелденеді.Кесінді [a,b] Ox
осіндегі D облысының проекциясы
болсын.Нүктелер (а,0) және (в,0)арқылы
вертикал x= ажәне x=b түзулерін жүргіземіз.D
жи ын ының дөңестігіне қарай оның
шекарасы
төрт
бөлікке
бөлінеді:x = a және x=bтүзулерінде жататын
және
теңдігі дедәлелденеді.Кесінді [a,b] Ox
осіндегі D облысының проекциясы
болсын.Нүктелер (а,0) және (в,0)арқылы
вертикал x= ажәне x=b түзулерін жүргіземіз.D
жи ын ының дөңестігіне қарай оның
шекарасы
төрт
бөлікке
бөлінеді:x = a және x=bтүзулерінде жататын
және
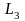 кесінділері
(олардың әрқайсысы тек,бір нүктеден
тұруы мүмкін және осы қисықтардың
арасындағы жолақта жататын
және
кесінділері
(олардың әрқайсысы тек,бір нүктеден
тұруы мүмкін және осы қисықтардың
арасындағы жолақта жататын
және
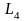 қисықтары.
және
қисықтарында
ч шамасы тұрақты,сондықтан
қисықтары.
және
қисықтарында
ч шамасы тұрақты,сондықтан
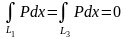 .Кез
келген
.Кез
келген
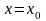 түзуі
түзуі
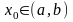 кезінде
(D-ның дөңестігіне қарай)
және
қисықтарының
әрқайсысын қатаң түрде бір нүктеде қиып
өтеді.Оларды тиісінше
кезінде
(D-ның дөңестігіне қарай)
және
қисықтарының
әрқайсысын қатаң түрде бір нүктеде қиып
өтеді.Оларды тиісінше
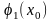 және
және
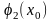 арқылы
белгілейміз,яғни
қисығы
арқылы
белгілейміз,яғни
қисығы
 функциясының
графигі ,ал
қисығы
функциясының
графигі ,ал
қисығы
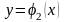 функциясының графигі болады.
функциясының графигі болады.
Қисық
L-дің бөліктік тегістігінен
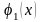 және
және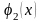 функцияларының бөлікті – тегістігі
шығады.Қисықсызықты интегралды Риман
интегралы арқылы өрнектелуі туралы
теоремадан мынаны аламыз:
функцияларының бөлікті – тегістігі
шығады.Қисықсызықты интегралды Риман
интегралы арқылы өрнектелуі туралы
теоремадан мынаны аламыз:

Бұдан
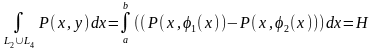
шығады.D - да функциясы үзіліссіз болғандықтан ,Ньютон – Лейбниц теоремасы бойынша:
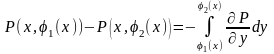 аламыз.Демек,
аламыз.Демек,
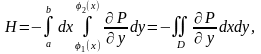
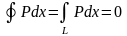 қарай,
қарай,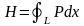 формуласы
дұрыс.
формуласы
дұрыс.
Грин формуласы интегралының аддитивтілігіне қарай дөңес облыстардың шектеулі бірігуі болатын облыстар үшін дұрыс екенін ескереміз.
Мысал.
1)Грин формуласына сәйкес D облысының ауданы қисықсызықты интеграл арқылы келесі түрде өрнектеледі:
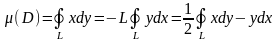
2)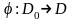 екі
жазық облыстың тегіс өзара бірмәнді
бейнелеуі болсын.Сондай – ақ
екі
жазық облыстың тегіс өзара бірмәнді
бейнелеуі болсын.Сондай – ақ
 бейнелеуінің
якобианы
облысында
таңьасын өзгертпейтін және
бейнелеуінің
якобианы
облысында
таңьасын өзгертпейтін және
 болсын.Сонымен
бірге,
-де
болсын.Сонымен
бірге,
-де
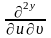 үзіліссіз
болсын.Сонда (1) мысалдың формуласынан
шығарып,D облысының өлшемді есептеуін
жүргіземіз:
үзіліссіз
болсын.Сонда (1) мысалдың формуласынан
шығарып,D облысының өлшемді есептеуін
жүргіземіз:
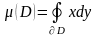 .
.
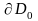 қисығының
қисығының
 түріндегі параметрлеуі берілген
болсын.Сонда
түріндегі параметрлеуі берілген
болсын.Сонда
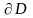
Қисығының
сәйкес параметрлеуі
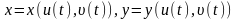 теңдеуімен беріледі.
теңдеуімен беріледі.
Қисықсызықты интегралдың Риман интегралы арқылы өрнектеуінен мынаны аламыз:
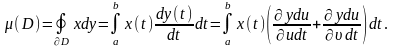
Бірақ соңғы интегралды қисығы бойынша интеграл ретінде беруге болады:яғни
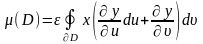 мұндағы
мұндағы
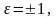 егер
және
қисықтарының
айналып өту бағыты бірдей болса,ал
егер
және
қисықтарының
айналып өту бағыты бірдей болса,ал
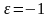 қарсы жағдайда .Соңғы интегралды
түрлендіріп ,Грин формуласын қолданып,мынаны
аламыз:
қарсы жағдайда .Соңғы интегралды
түрлендіріп ,Грин формуласын қолданып,мынаны
аламыз:
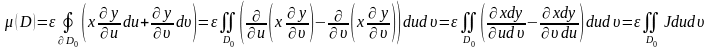 Якобиан
J таңбасын өзгертпейтін және
Якобиан
J таңбасын өзгертпейтін және
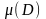 шамасы теріс емес болғандықтан,онда
шамасы теріс емес болғандықтан,онда
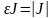 .Сондықтан
,
.Сондықтан
,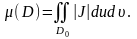 Сонымен
жазық облыстың ауданын қисықсызықты
координатада есептеу үшін формула
алынды.
Сонымен
жазық облыстың ауданын қисықсызықты
координатада есептеу үшін формула
алынды.
Дарбу қосындысы
Дөңес жиындағы тегіс бейнелеудің қасиеті
Еселі
интегралдарда айнымалыны алмастыруда
тегіс бейнелеудің кейбір қасиеттері
қажет болады. Функция
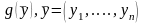 компактылы
өлшемді
компактылы
өлшемді
 облысында анықталған және
облысында анықталған және
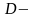 да
интегралданатын болсын.
да
интегралданатын болсын.
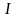 мына
интегралды білдіретін болсын
мына
интегралды білдіретін болсын
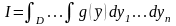 .
.
және
жиындарының ішкі нүктелерінің арасындағы
өзара бірмәнді сәйкестікті тағайындайтын,
жиынындағы
өлшемді компактының
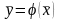 бейнелеуін қарастырамыз.
-де
анықталған
бейнелеуін қарастырамыз.
-де
анықталған
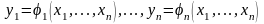
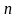 функцияның жүйесімен берілген
бейнелеуді ескереміз. Бұл функцияның
әрқайсысы
-де
барлық үзіліссіз дербес туындылы болады
деп есептейік.
функцияның жүйесімен берілген
бейнелеуді ескереміз. Бұл функцияның
әрқайсысы
-де
барлық үзіліссіз дербес туындылы болады
деп есептейік.
Ескерту.
1) Функция
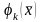 -де
анықталған қисықсызықты координата
деп аталады.
-де
анықталған қисықсызықты координата
деп аталады.
2) Бейнелеу
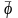 -дің
өзара бірмәнділік шарты:
облысының
ішкі нүктелері үшін
-дің
өзара бірмәнділік шарты:
облысының
ішкі нүктелері үшін
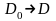 ,
облысының
әрбір нүктесінде осы бейнелеудің
якобиандары нөлден өзгеше болғанда
ғана қанағаттандырылады(кері бейнелеу
туралы теорема). Облыстағы тегіс бейнелеу
туралы тұжырымды құрамыз және дәлелдейміз.
,
облысының
әрбір нүктесінде осы бейнелеудің
якобиандары нөлден өзгеше болғанда
ғана қанағаттандырылады(кері бейнелеу
туралы теорема). Облыстағы тегіс бейнелеу
туралы тұжырымды құрамыз және дәлелдейміз.
Теорема
12.
дөңес және тұйық жиын және
жиынында
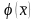 тегіс функция болсын. Сондай-ақ
тегіс функция болсын. Сондай-ақ
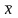 және
және
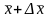 нүктелері
-ге
тиісті болсын. Онда мынадай
нүктелері
-ге
тиісті болсын. Онда мынадай
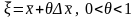 нүктесі табылады да,
нүктесі табылады да, болады.
болады.
Дәлелдеуі.
Бір
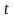 айнымалылы
айнымалылы
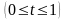
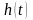 функциясын қарастырамыз:
функциясын қарастырамыз:

Мұнда
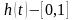 кесіндісіндегі тегіс функция.
кесіндісіндегі тегіс функция.
Олай
болса, оған шектеулі өсімшенің Лагранж
формуласын қолдануға болады. Онда
мынадай
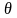 ,
,
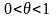 саны табылады да,
саны табылады да,
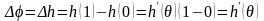 болады. Функция
күрделі функция
-дан
және күрделі функцияны дифференциалдау
ережесі бойынша мынаны аламыз:
болады. Функция
күрделі функция
-дан
және күрделі функцияны дифференциалдау
ережесі бойынша мынаны аламыз:
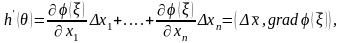 мұнда
мұнда
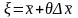 .
Дәлелденді.
.
Дәлелденді.
Теорема
13.
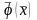 -
D облысындағы D0
дөңес компактың тегіс бейнелеуге болады.
Онда мынадай
-
D облысындағы D0
дөңес компактың тегіс бейнелеуге болады.
Онда мынадай
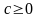 саны табылады да, кез-келген
саны табылады да, кез-келген
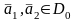 нүктелері үшін
нүктелері үшін
 теңсіздігі
дұрыс болады. Мұндағы
теңсіздігі
дұрыс болады. Мұндағы
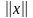 -евклидтік
метрикадағы (өлшемдегі) вектор ұзындығы.
-евклидтік
метрикадағы (өлшемдегі) вектор ұзындығы.
Дәлелденуі.
Теорема 12-ден
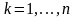 кезінде мынаны аламыз.
кезінде мынаны аламыз.
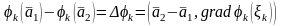
Мұндағы
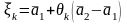 және
және
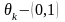 интервалының кейбір саны. Коши теңсіздігін
интервалының кейбір саны. Коши теңсіздігін
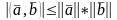 қолданып, мынаны аламыз:
қолданып, мынаны аламыз:
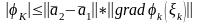 .
.
компакт
және
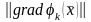 функциясы
-де
үзіліссіз болғандықтан, ол бұл компактіде
кейбір
функциясы
-де
үзіліссіз болғандықтан, ол бұл компактіде
кейбір
 тұрақтысымен
шектеледі. Осыны және сандық теңсіздікті
тұрақтысымен
шектеледі. Осыны және сандық теңсіздікті
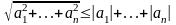 қолданып,
қолданып,
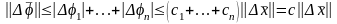 аламыз, мұндағы
аламыз, мұндағы
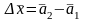 .
Дәлелденді.
.
Дәлелденді.
Бейнелеу
-дің
Якоби матрицасы
 арқылы белгілейік:
нүктесінде
арқылы белгілейік:
нүктесінде
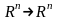 .
.
Анықтама
17. Вектор
-тің
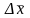 өсімшесінің
өсімшесінің
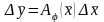 сызықтық бейнелеуі деп
бейнелеудің дифференциалын айтады және
сызықтық бейнелеуі деп
бейнелеудің дифференциалын айтады және
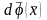 символымен белгіленеді.
символымен белгіленеді.
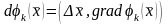 -
вектор.
Теорема 14.
-
вектор.
Теорема 14.
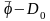 дөңес компактінің тегіс бейнелеуі және
дөңес компактінің тегіс бейнелеуі және
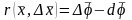 болсын. Онда келесі бірқалыпты шектің
орны бар
болсын. Онда келесі бірқалыпты шектің
орны бар
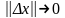 кезінде
кезінде
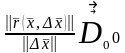 .
Басқаша айтқанда, мынадай
.
Басқаша айтқанда, мынадай
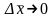 кезінде
кезінде
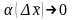 сандық функция табылады да, барлық
сандық функция табылады да, барлық
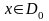 үшін
үшін
 теңсіздігі дұрыс болады.
теңсіздігі дұрыс болады.
Дәләлдеуі:
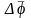 және
және
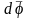 векторларының
векторларының
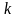 -шы
координатасын қарастырамыз. Анықтама
бойынша
-шы
координатасын қарастырамыз. Анықтама
бойынша
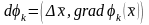 ,
ал Теорема 12 бойынша кейбір
,
ал Теорема 12 бойынша кейбір
 кезінде мынаны аламыз:
кезінде мынаны аламыз:
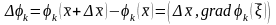 .
Олай болса,
.
Олай болса,
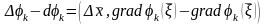 .
Енді
бейнелеуінің дербес туындысы
компактіде үзіліссіз болғандықтан,
онда
-де
оның бірқалыпты үзіліссіздігі ретінде
мынаны аламыз:
.
Енді
бейнелеуінің дербес туындысы
компактіде үзіліссіз болғандықтан,
онда
-де
оның бірқалыпты үзіліссіздігі ретінде
мынаны аламыз:
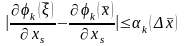 ,
мұндағы
,
мұндағы
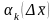 тек қана
-
ке тәуелді және
кезінде
тек қана
-
ке тәуелді және
кезінде
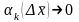 .
Бұдан Коши теңсіздігің қолданып мынаны
аламыз:
.
Бұдан Коши теңсіздігің қолданып мынаны
аламыз:
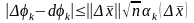 ,
олай болса,
,
олай болса,
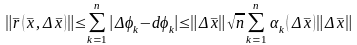 ,
әрі
кезінде
.
,
әрі
кезінде
.
Дәлелденді.
Еселі интегралдарға айнымалыны ауыстыру формуласы
Жордан бойынша өлшемді Риманның қос интегралы
Анықтама
15:
Жордан бойынша өлшенетін, шектелген D
облысының
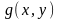 функциясын
Риманның жалпыланған қос интегралы деп
I санын айтады, егер кез-келген
функциясын
Риманның жалпыланған қос интегралы деп
I санын айтады, егер кез-келген
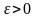 үшін
мынадай
үшін
мынадай
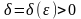 саны
табылып, әрбір
саны
табылып, әрбір
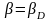 бөлінуі
үшін
бөлінуі
үшін
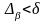 шартымен
шартымен
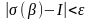 теңсіздігі
орындалса.
теңсіздігі
орындалса.
Жалпыланған
қос интегралды база бойынша шек ретінде
қарастыруға болады, Бұл базаны
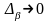 символымен
белгілейміз. Ол
символымен
белгілейміз. Ол
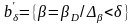 шартымен
анықталған
шартымен
анықталған
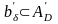 жалғауынан
құрылады. Шындығында да,
жалғауынан
құрылады. Шындығында да,
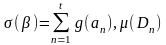 функциясы
функциясы
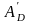 жиынында
анықталған, ал оның база бойынша шегі
және ол D обылысы бойынша жалпыланған
қос интеграл болады.
жиынында
анықталған, ал оның база бойынша шегі
және ол D обылысы бойынша жалпыланған
қос интеграл болады.
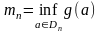 ,
,
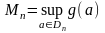 ,
,
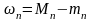 болсын.
Онда Дарбудың жоғарғы және төменгі
қосындысын келесі өрнекке сәйкес
анықтаймыз:
болсын.
Онда Дарбудың жоғарғы және төменгі
қосындысын келесі өрнекке сәйкес
анықтаймыз:
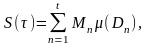
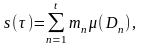 және
омега қосындысын
және
омега қосындысын
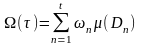 өрнегімен
анықтаймыз.
өрнегімен
анықтаймыз.
Кейбір
P тіктөртбұрышы үшін
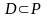 болсын.
болсын.
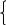
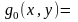
 деп
ұйғарып , барлық Р тіктөртбұрышын да
функциясын
анықтаймыз.
деп
ұйғарып , барлық Р тіктөртбұрышын да
функциясын
анықтаймыз.
Анықтама
16 :
Егер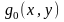 функциясы Р тіктөртбұрышында Риман
бойынша интегралданатын болса, онда
функциясының Р бойынша J қос интегралы
функциясының D жиыны бойынша Риман қос
интегралы деп аталады, яғни анықтама
бойынша
функциясы Р тіктөртбұрышында Риман
бойынша интегралданатын болса, онда
функциясының Р бойынша J қос интегралы
функциясының D жиыны бойынша Риман қос
интегралы деп аталады, яғни анықтама
бойынша
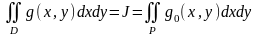 болады.
болады.
Теорема 6: Жалпыланған қос I интегралының бар болуы үшін, J интегралының бар болуы қажетті және жеткілікті, сонымен бәрге онда I=J.
Дәлелдеуі:
Тіктөртбұрыш P және J интегралы бар болсын. Онда интегралыдану критерийіне байланысты
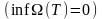 ,
кез-келген
үшін,
мынадай Т бөліну табылады да,
,
кез-келген
үшін,
мынадай Т бөліну табылады да,
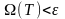 .
Т бөліну
тіктөртбұрыштарынан
тұрады.
.
Т бөліну
тіктөртбұрыштарынан
тұрады.
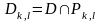 деп аламыз. Онда D жиынының
деп аламыз. Онда D жиынының
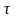 бөлінуін аламыз.
жиындағы
функциясының тербелісі
-дағы
оның тербеліснен аспайды, сондықтан
бөлінуін аламыз.
жиындағы
функциясының тербелісі
-дағы
оның тербеліснен аспайды, сондықтан
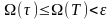 аламыз,
яғни интегралдану киртерийіне байланысты
жалпыланған I интегралы табылады.
Осыған ұқсас,
аламыз,
яғни интегралдану киртерийіне байланысты
жалпыланған I интегралы табылады.
Осыған ұқсас,
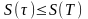 теңсіздігін
алуға болады, сондықтан
теңсіздігін
алуға болады, сондықтан
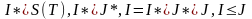 .
Дарбудың төменгі қосындысы үшін ұқсас
теңсіздіктерден
.
Дарбудың төменгі қосындысы үшін ұқсас
теңсіздіктерден
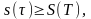
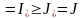 аламыз.
Осы теңсіздіктерден, I=J шығады. Қажеттілігі
дәлелденді.
аламыз.
Осы теңсіздіктерден, I=J шығады. Қажеттілігі
дәлелденді.Шектелген өлшемді D жиыны бойынша жалпыланған I интегралы бар болсын. D-ны құрайтын, Р тіктөртбұрышы бойынша функциясының I интегралының бар болатынын дәлелдеу керек. Интегралдану критерийінен, мынадай
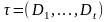 табылады
да,
табылады
да,
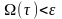 аламыз.
аламыз.
Әрбір
r=1,.. t үшін,
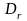 жиыны
өлшемді, сондықтан
жиыны
өлшемді, сондықтан
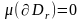 .
Олай болса,
тіктөртбұрышынан
құрылған, мынадай қарапайым F фигурасы
табыладыда, кем дегенде бір
.
Олай болса,
тіктөртбұрышынан
құрылған, мынадай қарапайым F фигурасы
табыладыда, кем дегенде бір
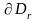 ,
r=1,…t шекарасының нүктесін құрайтын,
барлық
қосынды ауданы
,
r=1,…t шекарасының нүктесін құрайтын,
барлық
қосынды ауданы
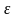 -нен
аспайды, яғни
-нен
аспайды, яғни
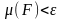 .
.
F
шекараның түзу сызықты кесіндісін Р
тіктөртбұрышының қабырғасымен қиылысқанша
созамыз. Осы тіктөртбұрыштың Т бөлінуін
аламыз. P/F- қа жататын тіктөртбұрыштардың
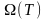 омега-қосыдысына
омега-қосыдысына
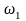 кірісі,
-нан
аспайды. F-те жататын сондай тіктөртбұрыштардың
-ға
кірісі,
-нан
аспайды. F-те жататын сондай тіктөртбұрыштардың
-ға
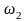 кірісі
кірісі
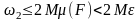 -нан
аспайды. Олай болса,
-нан
аспайды. Олай болса,
 .
.
Бұдан
тіктөртбұрыш бойынша функцияның
интегралдану критерийіне байланысты,
J интегралының бар болатыны шығады.
Осыған ұқсас, Дарбудың жоғарғы қосындысы
үшін талқылап, мына теңсіздікті аламыз:
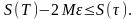 Олай
болса,
Олай
болса,
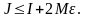 Еркін
түрде
оң санын таңдауымызға байланысты бұдан
Еркін
түрде
оң санын таңдауымызға байланысты бұдан
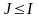 -ді
аламыз. Дарбудың төменгі қосындысы үшін
бағалаудан қарама-қарсы
-ді
аламыз. Дарбудың төменгі қосындысы үшін
бағалаудан қарама-қарсы
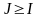 теңсіздігін аламыз. Сонымен, I=J. Дәлелденді.
теңсіздігін аламыз. Сонымен, I=J. Дәлелденді.
